湘教数学八下2.5.1矩形的性质 课件(13张PPT)
文档属性
| 名称 | 湘教数学八下2.5.1矩形的性质 课件(13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-27 00:00:00 | ||
图片预览



文档简介
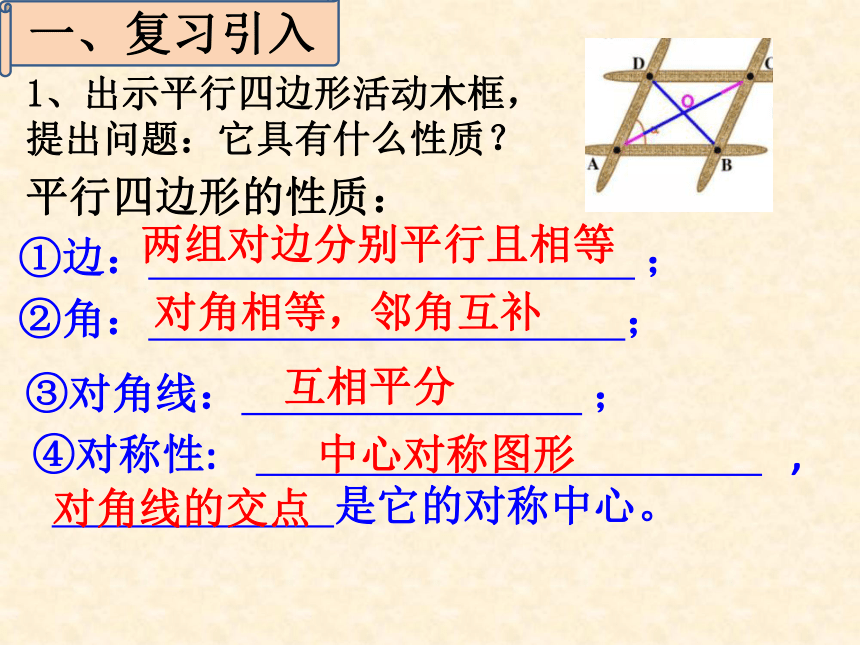
课件13张PPT。执教:蒋琳姣2.5 矩形的性质1、出示平行四边形活动木框,
提出问题:它具有什么性质?④对称性: ,
是它的对称中心。平行四边形的性质:①边: ;②角: ;③对角线: ;一、复习引入两组对边分别平行且相等对角相等,邻角互补互相平分对角线的交点中心对称图形 2.引入:演示推动平行四边形活动木框上
的点D,提出问题:你发现了什么?(1)木框随四个内角大小发生变动,但仍保持平行四边形形状。(2)在推动过程中,当一个内角变为直角时,
木框形状为特殊的平行四边形,即为小学已学
过的长方形,初中我们称为矩形,这是我们今天
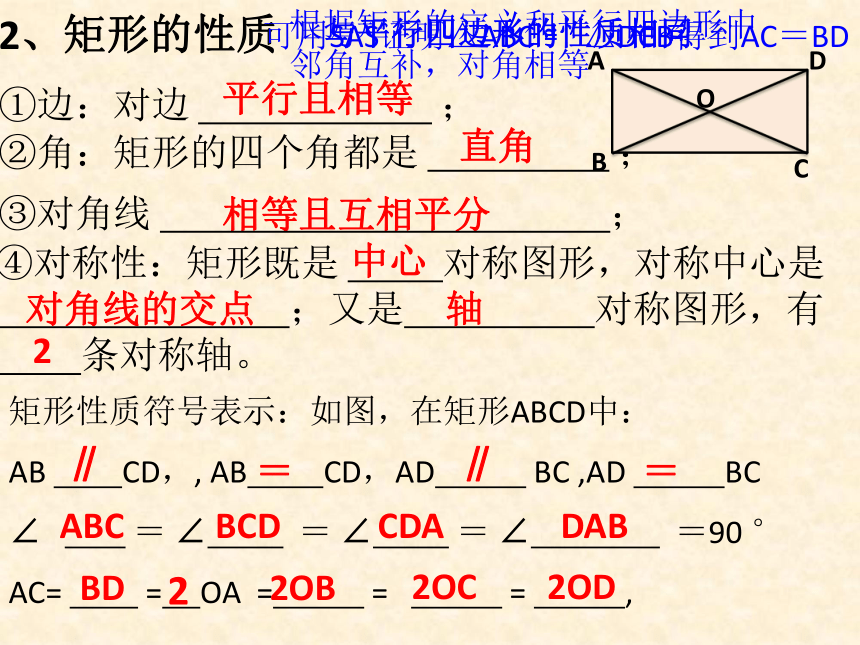
要探讨的内容。∠DAB=90°直角∠ABC=90 °二、自主学习,探究新知2、矩形的性质矩形性质符号表示:如图,在矩形ABCD中:
AB CD,, AB CD,AD BC ,AD BC
∠ = ∠ = ∠ = ∠ =90 °
AC= = OA = = = ,直角平行且相等相等且互相平分对角线的交点DABABCBCDCDA=∥∥=2OC2OD2OBBD2②角:矩形的四个角都是 ;①边:对边 ;③对角线 ; ④对称性:矩形既是 对称图形,对称中心是
;又是 对称图形,有
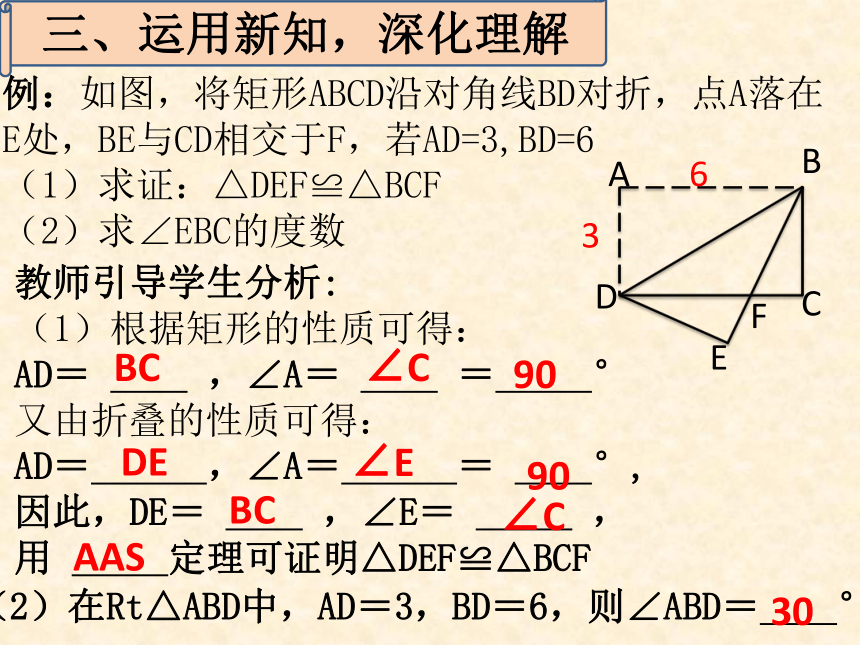
条对称轴。 中心轴与平行四边形的性质相同根据矩形的定义和平行四边形中邻角互补,对角相等可用SAS证明△ABC ≌ △DCB得到AC=BD2三、运用新知,深化理解例:如图,将矩形ABCD沿对角线BD对折,点A落在
E处,BE与CD相交于F,若AD=3,BD=6
(1)求证:△DEF≌△BCF
(2)求∠EBC的度数教师引导学生分析:
(1)根据矩形的性质可得:
AD= ,∠A= = °
又由折叠的性质可得:
AD= ,∠A= = °,
因此,DE= ,∠E= ,
用 定理可证明△DEF≌△BCF(2)在Rt△ABD中,AD=3,BD=6,则∠ABD= °BC∠C90DE∠E90BC∠CAAS3036(1)证明:∵在矩形ABCD中
∴AD=BC , ∠A= ∠C=90 °
又由折叠的性质得:
AD=DE ,∠A= ∠E=90 °
∴BC=DE , ∠C= ∠E=90 °
在△DEF与 △BCF中
∠C= ∠E=90 °, ∠DFE= ∠BCF, BC=DE
△DEF ≌ △BCF(AAS)
(2)在Rt △ABD中,AD=3,BD=6
∴ ∠ABD=30 °
又由折叠的性质得: ∠EBD=∠ABD =30 °
∴ ∠EBC= ∠ABC- ∠EBD-∠ABD
= 90 °- 30 °- 30 °=30 °
四、当堂检测,运用新知2.下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线互相垂直AD3、已知矩形的两边长分别为8和6,则矩形的对角线长为 .4、如图,在矩形ABCD中,AC与BD相交于点O,AB=3cm,BC=4cm 则AC= cm,BO= cm,
矩形的周长为 cm,
矩形的面积为 cm28610103452.5矩形的周长=2(AB+BC)=2(3+4)=14(cm)14矩形的面积=AB●BC=3×4=12( cm2 )12五、课堂小结1.矩形是如何从平行四边形演变而来的?四边形、平行四边形、矩形的从属关系
两组对边分别平行 平行四边形有一个角是直角 矩形(1)边的性质:对边平行且相等。
(2)角的性质:四个角都是直角。
(3)对角线性质:对角线互相平分且相等。
(4)对称性:矩形是轴对称图形。2.矩形的性质有哪些?作业:教材 62页 习题 2.5
A组 第 1 题
谢谢大家再见
提出问题:它具有什么性质?④对称性: ,
是它的对称中心。平行四边形的性质:①边: ;②角: ;③对角线: ;一、复习引入两组对边分别平行且相等对角相等,邻角互补互相平分对角线的交点中心对称图形 2.引入:演示推动平行四边形活动木框上
的点D,提出问题:你发现了什么?(1)木框随四个内角大小发生变动,但仍保持平行四边形形状。(2)在推动过程中,当一个内角变为直角时,
木框形状为特殊的平行四边形,即为小学已学
过的长方形,初中我们称为矩形,这是我们今天
要探讨的内容。∠DAB=90°直角∠ABC=90 °二、自主学习,探究新知2、矩形的性质矩形性质符号表示:如图,在矩形ABCD中:
AB CD,, AB CD,AD BC ,AD BC
∠ = ∠ = ∠ = ∠ =90 °
AC= = OA = = = ,直角平行且相等相等且互相平分对角线的交点DABABCBCDCDA=∥∥=2OC2OD2OBBD2②角:矩形的四个角都是 ;①边:对边 ;③对角线 ; ④对称性:矩形既是 对称图形,对称中心是
;又是 对称图形,有
条对称轴。 中心轴与平行四边形的性质相同根据矩形的定义和平行四边形中邻角互补,对角相等可用SAS证明△ABC ≌ △DCB得到AC=BD2三、运用新知,深化理解例:如图,将矩形ABCD沿对角线BD对折,点A落在
E处,BE与CD相交于F,若AD=3,BD=6
(1)求证:△DEF≌△BCF
(2)求∠EBC的度数教师引导学生分析:
(1)根据矩形的性质可得:
AD= ,∠A= = °
又由折叠的性质可得:
AD= ,∠A= = °,
因此,DE= ,∠E= ,
用 定理可证明△DEF≌△BCF(2)在Rt△ABD中,AD=3,BD=6,则∠ABD= °BC∠C90DE∠E90BC∠CAAS3036(1)证明:∵在矩形ABCD中
∴AD=BC , ∠A= ∠C=90 °
又由折叠的性质得:
AD=DE ,∠A= ∠E=90 °
∴BC=DE , ∠C= ∠E=90 °
在△DEF与 △BCF中
∠C= ∠E=90 °, ∠DFE= ∠BCF, BC=DE
△DEF ≌ △BCF(AAS)
(2)在Rt △ABD中,AD=3,BD=6
∴ ∠ABD=30 °
又由折叠的性质得: ∠EBD=∠ABD =30 °
∴ ∠EBC= ∠ABC- ∠EBD-∠ABD
= 90 °- 30 °- 30 °=30 °
四、当堂检测,运用新知2.下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线互相垂直AD3、已知矩形的两边长分别为8和6,则矩形的对角线长为 .4、如图,在矩形ABCD中,AC与BD相交于点O,AB=3cm,BC=4cm 则AC= cm,BO= cm,
矩形的周长为 cm,
矩形的面积为 cm28610103452.5矩形的周长=2(AB+BC)=2(3+4)=14(cm)14矩形的面积=AB●BC=3×4=12( cm2 )12五、课堂小结1.矩形是如何从平行四边形演变而来的?四边形、平行四边形、矩形的从属关系
两组对边分别平行 平行四边形有一个角是直角 矩形(1)边的性质:对边平行且相等。
(2)角的性质:四个角都是直角。
(3)对角线性质:对角线互相平分且相等。
(4)对称性:矩形是轴对称图形。2.矩形的性质有哪些?作业:教材 62页 习题 2.5
A组 第 1 题
谢谢大家再见
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
