湘教数学八下3.3用坐标表示轴对称 课件(20张PPT)
文档属性
| 名称 | 湘教数学八下3.3用坐标表示轴对称 课件(20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 557.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-27 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
3.3 轴对称和平移的坐标表示
第1课时 轴对称的坐标表示
学习目标
1.在平面直角坐标系中,探索关于x轴、y轴对称的点的坐标规律,并熟练运用规律解题。
2.利用关于x轴、y轴对称的点的坐标的规律,能作关于x轴、y轴对称的图形.
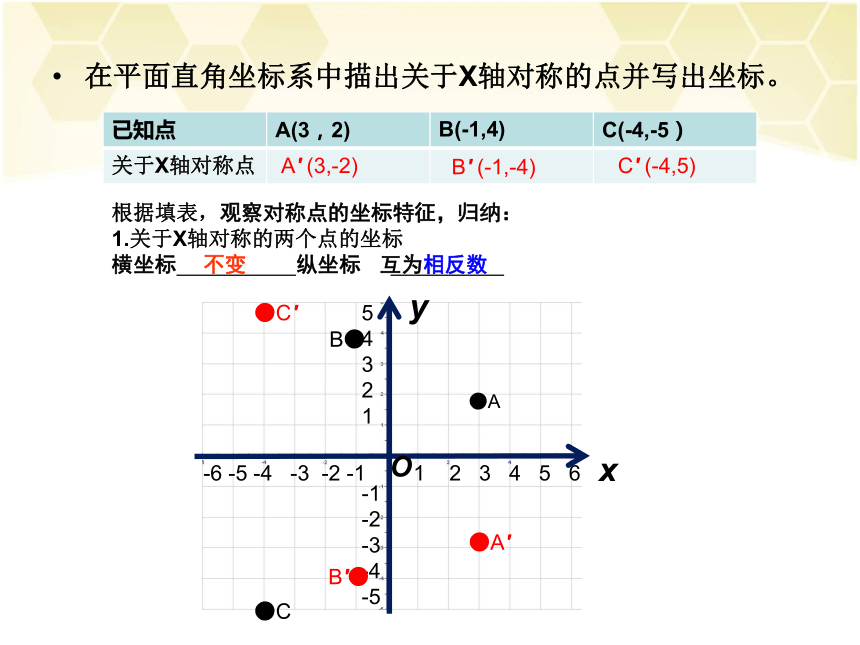
在平面直角坐标系中描出关于X轴对称的点并写出坐标。
已知点 A(3,2) B(-1,4) C(-4,-5)
关于X轴对称点
根据填表,观察对称点的坐标特征,归纳:
1.关于X轴对称的两个点的坐标
横坐标 纵坐标
x
y
O
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6
5
4
3
2
1
-1
-2
-3
-4
-5
A′ (3,-2)
B′ (-1,-4)
C′ (-4,5)
●A
●A′
B′●
B●
●C
●C′
不变
互为相反数
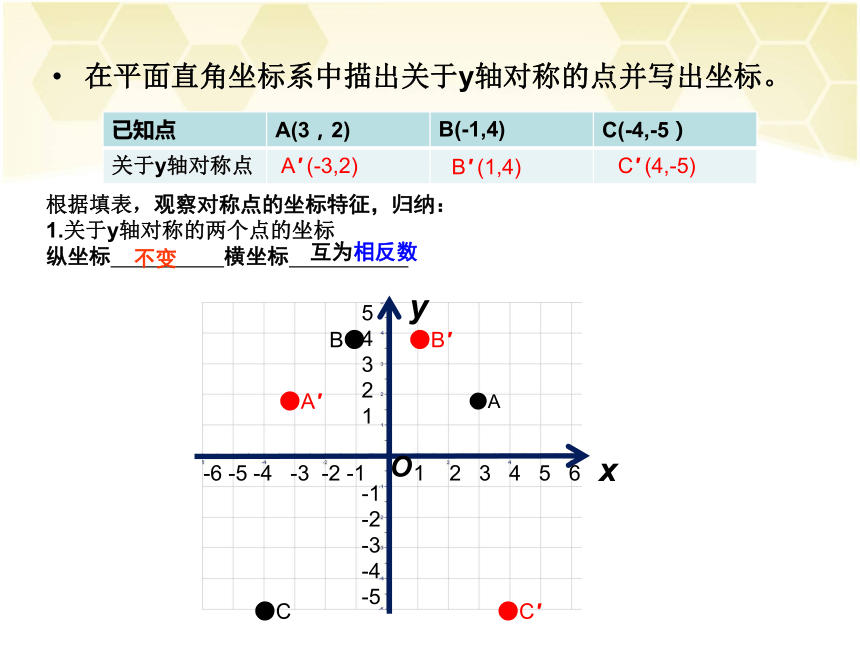
在平面直角坐标系中描出关于y轴对称的点并写出坐标。
已知点 A(3,2) B(-1,4) C(-4,-5)
关于y轴对称点
根据填表,观察对称点的坐标特征,归纳:
1.关于y轴对称的两个点的坐标
纵坐标 横坐标
x
y
O
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6
5
4
3
2
1
-1
-2
-3
-4
-5
A′ (-3,2)
B′ (1,4)
C′ (4,-5)
●A
●A′
●B′
B●
●C
●C′
不变
互为相反数
归纳:
关于X轴对称:横(x)坐标不变,纵(y)坐标互为相反数
关于y轴对称:纵(y)坐标不变,横(x)坐标互为相反数
关于谁对称谁不变,另一个互为相反
点(a, b)关于y轴对称的点的坐标为_______.
点(a, b)关于x轴对称的点的坐标为_______.
一般地,在平面直角坐标系中,
(a, - b)
(- a, b)
关于谁对称谁不变,另一个互为相反
●
C(0,3)
●
B
(4,0)
o
x
y
轴线上的点关于那个轴
线的对称点就是本身
●
(0,0)
(4,0)
(0,3)
原点的对称点就是原点
C(0,3)关于y轴对称
的坐标是——
B(4,0)关于X轴对称
的坐标是——
关于X轴y轴对称的特殊点
关于谁对称谁不变,另一个互为相反
应用
口答:
1)点B(2,-3)关于x轴对称的点的坐标是________;
2)点A(-5,3)关于y轴对称的点的坐标是________.
3)点A(1,-2)关于X轴对称的点的坐标是( )
A (1,-2) B (-1,2) C (-1,-2) D (1,2)
4)已知点A(-2,-3)与点B关于x轴对称,则点B在( )
A 第一象限 B第二象限 C第三象限 D第四象限
5)下列各组点关于y轴对称的是( )
A(0,10)与(0,-10) B (-3,-2) 与(3,-2)
C (-3,-2)与(3,2) D(-3,-2)与(-3,2)
(2,3)
(5,3)
D
B
B
关于x轴y轴对称求对称点的坐标
关于谁对称谁不变,另一个互为相反
应用:关于x轴y轴对称,求字母
已知点P(a-1,5)和P ′ (2,b-1):
1)若点P和P ′ 关于x轴对称,则a+b的值为
2)若点P和P ′ 关于y轴对称,则a+b的值为
坐标关系
列出方程
解未知数
-1
5
.
.
关于谁对称谁不变,另一个互为相反
6)已知点P(3,a)关于y轴对称的点的为Q(b,2),则ab= .
7)已知A(m-1,3)与点B(2,n+1)关于x轴对称,
则m= n= .
8)已知点M(2a+b,5),N(-7,b)关于y轴对称,
则b = .
3
-4
-6
应用:关于x轴y轴对称,求字母的值
a
5
关于谁对称谁不变,另一个互为相反
做一做
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4),B(1,2),C(5,2).
(1)作出△ABC关于y轴的轴对称图形,并写出其顶点坐标.
(2)作出△ABC关于x轴的轴对称图形,并写出其顶点坐标.
B
●
●
●
C
A
做一个图形关于坐标轴的轴对称图形,怎样画最简便呢?
1、作出三角形三个顶点关于坐标轴的对称点.
2、连接三个对称点,所得图形即为所求对称图形.
o
x
y
(1)作出△ABC关于y轴的轴对称图形,并写出其顶点坐标.
A(2,4),
B(1,2),
C(5,2).
B
●
●
●
C
A
●
A1(-2,4)
●
C1(-5,2)
●
B1(-1,2)
●
B2(1,-2)
●
C2(5,-2)
●
A2(-2,4)
o
x
y
一找二描三连线
(2,4),
(1,2),
(5,2).
关于谁对称谁不变,另一个互为相反
(1)如图,分别作出点A,B,C关于y轴的对称点A1,B1,
C1,并连接这三点,则△A1B1C1即为所求作的图形.此时
其顶点坐标分别为A1(-2,4),B1(-1,2),C1(-5,2).
(2)类似(1)的做法,可作出△ABC关于x轴的轴对称
图形△A2B2C2,其顶点坐标分别为A2(2,-4),B2(1,-2),C2(5,-2).
作一个点关于坐标轴的对
称点,你有什么窍门吗?
小知识
关于x轴对称x不变,y变相反
关于y轴对称y不变,x变相反
关于谁对称谁不变,另一个互为相反
练习
已知矩形ABCD的顶点坐标分别A(-7,-2),B(-7,-5),C(-3,-5),D(-3,-2),以y轴为对称轴作轴反射,矩形ABCD的像为矩形A′B′C′D′,求矩形A′B′C′D′的顶点坐标.
解:矩形A′B′C′D′的顶点坐标分别是A′(7,-2),B′(7,-5)C′(3,-5),D′(3,-2).
结论
把一个轴对称图形画在直角坐标系中,怎样画最简便呢?
1、使对称轴与坐标轴重合
2、画出一侧的关键点,并求坐标
3、利用坐标关系,求另一侧关键点坐标
4、描点、连线
小结
学习了在平面直角坐标系中,关于x轴和y 轴对称的点的坐标的特点.
这节课你学到了什么知识?
关于x轴对称的点x坐标不变,y坐标互为相反数.
关于y轴对称的点y坐标不变,x坐标互为相反数.
作业:
练习册
3.3 轴对称和平移的坐标表示
第1课时 轴对称的坐标表示
学习目标
1.在平面直角坐标系中,探索关于x轴、y轴对称的点的坐标规律,并熟练运用规律解题。
2.利用关于x轴、y轴对称的点的坐标的规律,能作关于x轴、y轴对称的图形.
在平面直角坐标系中描出关于X轴对称的点并写出坐标。
已知点 A(3,2) B(-1,4) C(-4,-5)
关于X轴对称点
根据填表,观察对称点的坐标特征,归纳:
1.关于X轴对称的两个点的坐标
横坐标 纵坐标
x
y
O
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6
5
4
3
2
1
-1
-2
-3
-4
-5
A′ (3,-2)
B′ (-1,-4)
C′ (-4,5)
●A
●A′
B′●
B●
●C
●C′
不变
互为相反数
在平面直角坐标系中描出关于y轴对称的点并写出坐标。
已知点 A(3,2) B(-1,4) C(-4,-5)
关于y轴对称点
根据填表,观察对称点的坐标特征,归纳:
1.关于y轴对称的两个点的坐标
纵坐标 横坐标
x
y
O
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6
5
4
3
2
1
-1
-2
-3
-4
-5
A′ (-3,2)
B′ (1,4)
C′ (4,-5)
●A
●A′
●B′
B●
●C
●C′
不变
互为相反数
归纳:
关于X轴对称:横(x)坐标不变,纵(y)坐标互为相反数
关于y轴对称:纵(y)坐标不变,横(x)坐标互为相反数
关于谁对称谁不变,另一个互为相反
点(a, b)关于y轴对称的点的坐标为_______.
点(a, b)关于x轴对称的点的坐标为_______.
一般地,在平面直角坐标系中,
(a, - b)
(- a, b)
关于谁对称谁不变,另一个互为相反
●
C(0,3)
●
B
(4,0)
o
x
y
轴线上的点关于那个轴
线的对称点就是本身
●
(0,0)
(4,0)
(0,3)
原点的对称点就是原点
C(0,3)关于y轴对称
的坐标是——
B(4,0)关于X轴对称
的坐标是——
关于X轴y轴对称的特殊点
关于谁对称谁不变,另一个互为相反
应用
口答:
1)点B(2,-3)关于x轴对称的点的坐标是________;
2)点A(-5,3)关于y轴对称的点的坐标是________.
3)点A(1,-2)关于X轴对称的点的坐标是( )
A (1,-2) B (-1,2) C (-1,-2) D (1,2)
4)已知点A(-2,-3)与点B关于x轴对称,则点B在( )
A 第一象限 B第二象限 C第三象限 D第四象限
5)下列各组点关于y轴对称的是( )
A(0,10)与(0,-10) B (-3,-2) 与(3,-2)
C (-3,-2)与(3,2) D(-3,-2)与(-3,2)
(2,3)
(5,3)
D
B
B
关于x轴y轴对称求对称点的坐标
关于谁对称谁不变,另一个互为相反
应用:关于x轴y轴对称,求字母
已知点P(a-1,5)和P ′ (2,b-1):
1)若点P和P ′ 关于x轴对称,则a+b的值为
2)若点P和P ′ 关于y轴对称,则a+b的值为
坐标关系
列出方程
解未知数
-1
5
.
.
关于谁对称谁不变,另一个互为相反
6)已知点P(3,a)关于y轴对称的点的为Q(b,2),则ab= .
7)已知A(m-1,3)与点B(2,n+1)关于x轴对称,
则m= n= .
8)已知点M(2a+b,5),N(-7,b)关于y轴对称,
则b = .
3
-4
-6
应用:关于x轴y轴对称,求字母的值
a
5
关于谁对称谁不变,另一个互为相反
做一做
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4),B(1,2),C(5,2).
(1)作出△ABC关于y轴的轴对称图形,并写出其顶点坐标.
(2)作出△ABC关于x轴的轴对称图形,并写出其顶点坐标.
B
●
●
●
C
A
做一个图形关于坐标轴的轴对称图形,怎样画最简便呢?
1、作出三角形三个顶点关于坐标轴的对称点.
2、连接三个对称点,所得图形即为所求对称图形.
o
x
y
(1)作出△ABC关于y轴的轴对称图形,并写出其顶点坐标.
A(2,4),
B(1,2),
C(5,2).
B
●
●
●
C
A
●
A1(-2,4)
●
C1(-5,2)
●
B1(-1,2)
●
B2(1,-2)
●
C2(5,-2)
●
A2(-2,4)
o
x
y
一找二描三连线
(2,4),
(1,2),
(5,2).
关于谁对称谁不变,另一个互为相反
(1)如图,分别作出点A,B,C关于y轴的对称点A1,B1,
C1,并连接这三点,则△A1B1C1即为所求作的图形.此时
其顶点坐标分别为A1(-2,4),B1(-1,2),C1(-5,2).
(2)类似(1)的做法,可作出△ABC关于x轴的轴对称
图形△A2B2C2,其顶点坐标分别为A2(2,-4),B2(1,-2),C2(5,-2).
作一个点关于坐标轴的对
称点,你有什么窍门吗?
小知识
关于x轴对称x不变,y变相反
关于y轴对称y不变,x变相反
关于谁对称谁不变,另一个互为相反
练习
已知矩形ABCD的顶点坐标分别A(-7,-2),B(-7,-5),C(-3,-5),D(-3,-2),以y轴为对称轴作轴反射,矩形ABCD的像为矩形A′B′C′D′,求矩形A′B′C′D′的顶点坐标.
解:矩形A′B′C′D′的顶点坐标分别是A′(7,-2),B′(7,-5)C′(3,-5),D′(3,-2).
结论
把一个轴对称图形画在直角坐标系中,怎样画最简便呢?
1、使对称轴与坐标轴重合
2、画出一侧的关键点,并求坐标
3、利用坐标关系,求另一侧关键点坐标
4、描点、连线
小结
学习了在平面直角坐标系中,关于x轴和y 轴对称的点的坐标的特点.
这节课你学到了什么知识?
关于x轴对称的点x坐标不变,y坐标互为相反数.
关于y轴对称的点y坐标不变,x坐标互为相反数.
作业:
练习册
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
