湘教数学八下4.4求一次函数的解析式 课件(16张PPT)
文档属性
| 名称 | 湘教数学八下4.4求一次函数的解析式 课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-27 15:56:49 | ||
图片预览




文档简介
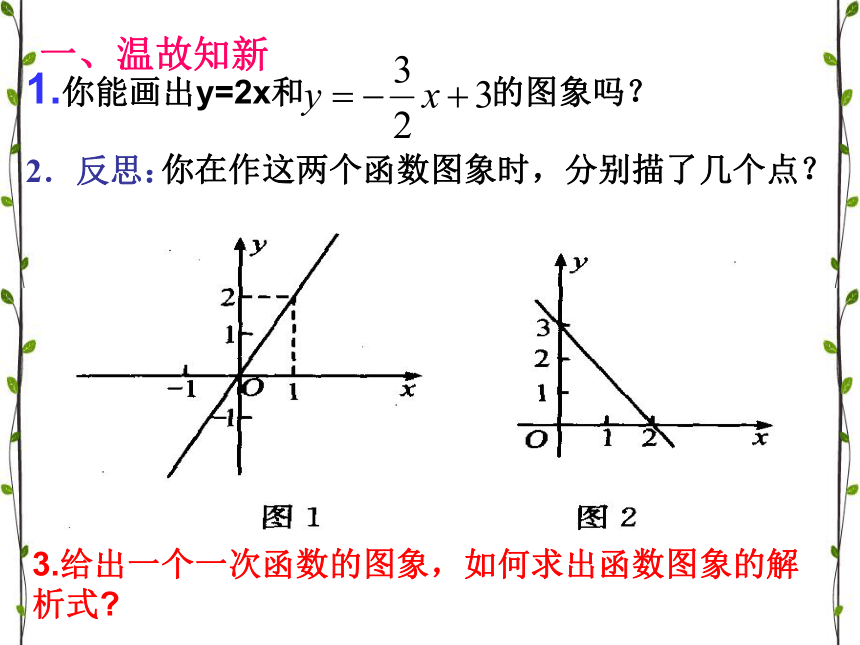
课件16张PPT。4.4求一次函数的解析式一、温故知新
3.给出一个一次函数的图象,如何求出函数图象的解析式?2、分析与思考: 图1是经过 的一条直线,因此是 ,可设它的表达式为 将点 代入表达式求得 ,从而确定该函数的表达式为 。
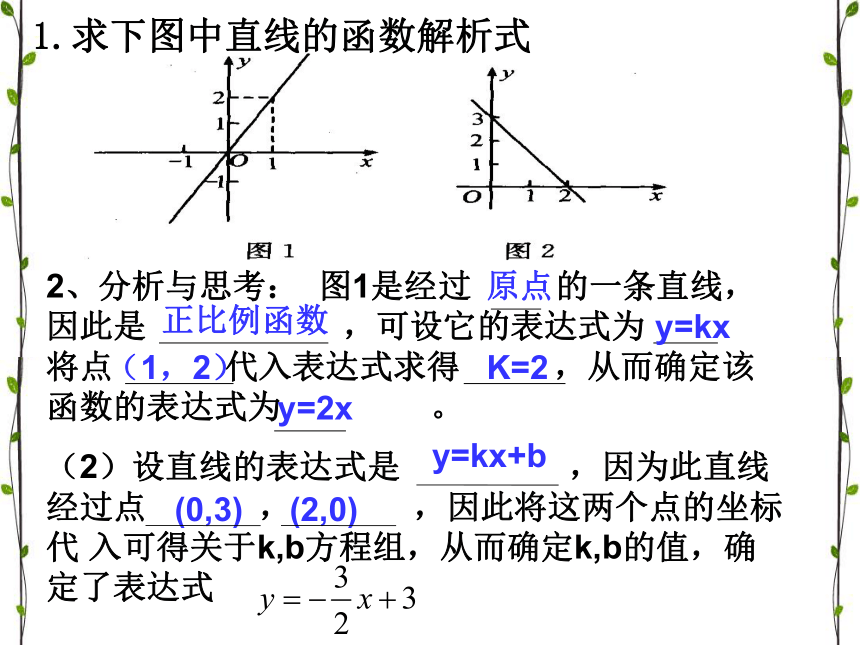
(2)设直线的表达式是 ,因为此直线经过点 , ,因此将这两个点的坐标代 入可得关于k,b方程组,从而确定k,b的值,确定了表达式 1.求下图中直线的函数解析式 (1,2)y=2xK=2y=kxy=kx+b(0,3)(2,0)正比例函数原点确定一次函数的表达式需要几个条件?确定正比例函数的表达式需要( )个
条件,确定一次函数(正比例函数外的一次函数)的表达式需要( )个条件.
反思小结12例1:已知正比例函数 y= kx,(k≠0) 的图象经过点(-2,4).求这个正比例函数的解析式.三、初步应用,感悟新知因为图象过点(-2,4) ,所以这点的坐标必适合解析式解:把x=-2,y=4;代入上式得:
-2k=4
解得:k=-2
∴这个正比例函数的解析式为:y=-2x
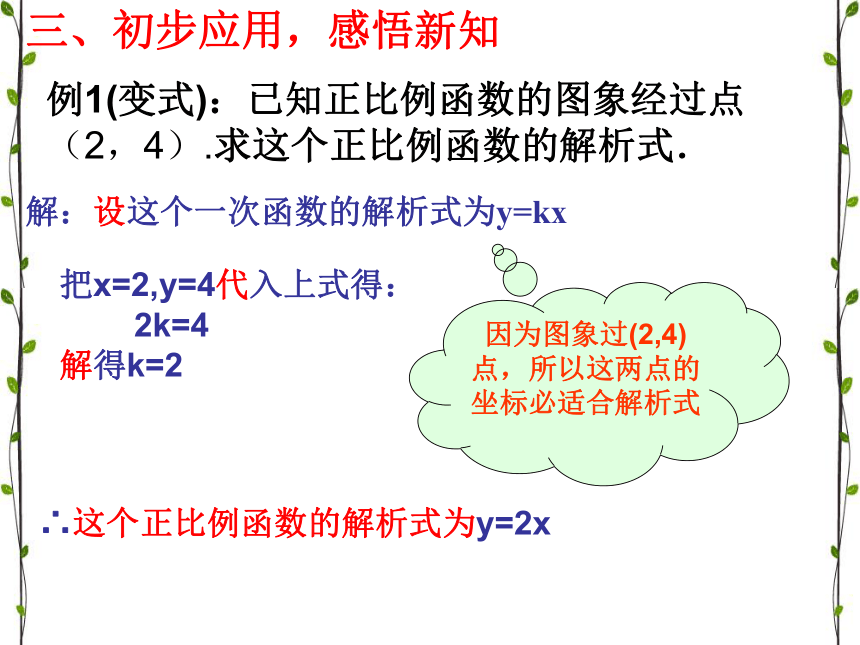
例1(变式):已知正比例函数的图象经过点
(2,4).求这个正比例函数的解析式.例1(变式):已知正比例函数的图象经过点
(2,4).求这个正比例函数的解析式.
解:设这个一次函数的解析式为y=kx∴这个正比例函数的解析式为y=2x三、初步应用,感悟新知因为图象过(2,4)点,所以这两点的坐标必适合解析式把x=2,y=4代入上式得:
2k=4
解得k=2
象这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法.小结归纳 你能归纳出待定系数法求函数解析式的基本步骤吗?例2:已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式. 初步应用,感悟新知 解:设这个一次函数的解析式为
y=kx+b把x=3,y=5;x=-4,y=-93k+b=5 分别代入上式得-4k+b=-9解得∴一次函数的解析式为y=2x-1一设二代三解四还原变式1.已知一次函数的图象如下图,写出它的关系式. 解 :设y=kx+b(k≠0).
由直线经过点(2,0),(0,-3)得解得 变式2.若一次函数的图象经过点 A(2,0)且与直线y=-x+3平行,求其解析式解:设这个一次函数的解析式为y=kx+b. ∵与直线y= -x+3平行
∴k= -1. 将k= -1,点A(2,0)代入y=kx+b得:
-1×2+b=0
解得:b=2 ∴一次函数的解析式为:y= -x+2变式3.小明根据某个一次函数关系式填写了下表:其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是多少?解:设这个一次函数的解析式为y=kx+b. -2k+b=3
b=1 ∴这个一次函数的解析式为y=-x+1把x=-2,y=3;x=0,y=1分别代入上式得:解得 k=-1
b=1 ∴当x=-1时.y=-(-1)+1=2课堂小结待定系数法 根据已知的自变量与函数的对应值,可以利用待定系数法确定一次函数的解析式。具体步骤如下:
1、设:函数解析式的一般形式(正比例函数设为y=kx,一次函数设为y=kx+b),其中包括未知的系数(需要确定这些系数,因此叫做待定系数);
2、代:把自变量与函数的对应值(可能是以函数图象上的点的坐标的形式给出)代入所设的函数解析式中,列出关于待定系数的方程或方程组。(有几个系数,就要有几个方程)
3、解:解方程或方程组,求出待定系数的值。
4、还原:写出所求函数的解析式。y=kx+b1. 已知弹簧的长度y(cm)在一定的限度内是所挂重物质量x(千克)的一次函数,现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米.求这个一次函数的关系式.设一次函数的表达式为_______________,解:y=kx+b(k≠0)根据题意,得b=64k+b=7.2解得:k=0.3b=6∴ 函数的解析式为 y= 0.3x +6拓展应用拓展应用用坐标表示线段长度时应用绝对值符号。六、课堂小结待定系数法1、通过这节课的学习,你知道利用什么方法确 定正比例函数或一次函数的解析式吗?
2、你还记得利用待定系数法确定函数解析式的一般步骤吗?
一设二代
三解四还原3、体验了数形结合思想在解决函数问题作用!
3.给出一个一次函数的图象,如何求出函数图象的解析式?2、分析与思考: 图1是经过 的一条直线,因此是 ,可设它的表达式为 将点 代入表达式求得 ,从而确定该函数的表达式为 。
(2)设直线的表达式是 ,因为此直线经过点 , ,因此将这两个点的坐标代 入可得关于k,b方程组,从而确定k,b的值,确定了表达式 1.求下图中直线的函数解析式 (1,2)y=2xK=2y=kxy=kx+b(0,3)(2,0)正比例函数原点确定一次函数的表达式需要几个条件?确定正比例函数的表达式需要( )个
条件,确定一次函数(正比例函数外的一次函数)的表达式需要( )个条件.
反思小结12例1:已知正比例函数 y= kx,(k≠0) 的图象经过点(-2,4).求这个正比例函数的解析式.三、初步应用,感悟新知因为图象过点(-2,4) ,所以这点的坐标必适合解析式解:把x=-2,y=4;代入上式得:
-2k=4
解得:k=-2
∴这个正比例函数的解析式为:y=-2x
例1(变式):已知正比例函数的图象经过点
(2,4).求这个正比例函数的解析式.例1(变式):已知正比例函数的图象经过点
(2,4).求这个正比例函数的解析式.
解:设这个一次函数的解析式为y=kx∴这个正比例函数的解析式为y=2x三、初步应用,感悟新知因为图象过(2,4)点,所以这两点的坐标必适合解析式把x=2,y=4代入上式得:
2k=4
解得k=2
象这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法.小结归纳 你能归纳出待定系数法求函数解析式的基本步骤吗?例2:已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式. 初步应用,感悟新知 解:设这个一次函数的解析式为
y=kx+b把x=3,y=5;x=-4,y=-93k+b=5 分别代入上式得-4k+b=-9解得∴一次函数的解析式为y=2x-1一设二代三解四还原变式1.已知一次函数的图象如下图,写出它的关系式. 解 :设y=kx+b(k≠0).
由直线经过点(2,0),(0,-3)得解得 变式2.若一次函数的图象经过点 A(2,0)且与直线y=-x+3平行,求其解析式解:设这个一次函数的解析式为y=kx+b. ∵与直线y= -x+3平行
∴k= -1. 将k= -1,点A(2,0)代入y=kx+b得:
-1×2+b=0
解得:b=2 ∴一次函数的解析式为:y= -x+2变式3.小明根据某个一次函数关系式填写了下表:其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是多少?解:设这个一次函数的解析式为y=kx+b. -2k+b=3
b=1 ∴这个一次函数的解析式为y=-x+1把x=-2,y=3;x=0,y=1分别代入上式得:解得 k=-1
b=1 ∴当x=-1时.y=-(-1)+1=2课堂小结待定系数法 根据已知的自变量与函数的对应值,可以利用待定系数法确定一次函数的解析式。具体步骤如下:
1、设:函数解析式的一般形式(正比例函数设为y=kx,一次函数设为y=kx+b),其中包括未知的系数(需要确定这些系数,因此叫做待定系数);
2、代:把自变量与函数的对应值(可能是以函数图象上的点的坐标的形式给出)代入所设的函数解析式中,列出关于待定系数的方程或方程组。(有几个系数,就要有几个方程)
3、解:解方程或方程组,求出待定系数的值。
4、还原:写出所求函数的解析式。y=kx+b1. 已知弹簧的长度y(cm)在一定的限度内是所挂重物质量x(千克)的一次函数,现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米.求这个一次函数的关系式.设一次函数的表达式为_______________,解:y=kx+b(k≠0)根据题意,得b=64k+b=7.2解得:k=0.3b=6∴ 函数的解析式为 y= 0.3x +6拓展应用拓展应用用坐标表示线段长度时应用绝对值符号。六、课堂小结待定系数法1、通过这节课的学习,你知道利用什么方法确 定正比例函数或一次函数的解析式吗?
2、你还记得利用待定系数法确定函数解析式的一般步骤吗?
一设二代
三解四还原3、体验了数形结合思想在解决函数问题作用!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
