人教版A版选修4—4 1.1.平面直角坐标系(共24张ppt)
文档属性
| 名称 | 人教版A版选修4—4 1.1.平面直角坐标系(共24张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 21:07:48 | ||
图片预览





文档简介
课件24张PPT。面角直平坐标系 笛卡尔,法国伟大的哲学家、物理学家、数学家。解析几何的创始人。1637年,他发表了《几何学》,创立了直角坐标系,把相互对立的“数”与“形”统一了起来,人们称他为“近代科学的始祖”。故事中发现笛卡尔声响定位问题 某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到一声巨响,正东观测点听到巨响的时间比其他两个观测点晚4s,已知各观测点到中心的距离都是1020m,试确定该巨响的位置。(假定当时声音传播的速度为340m/s,各相关点均在同一平面上)
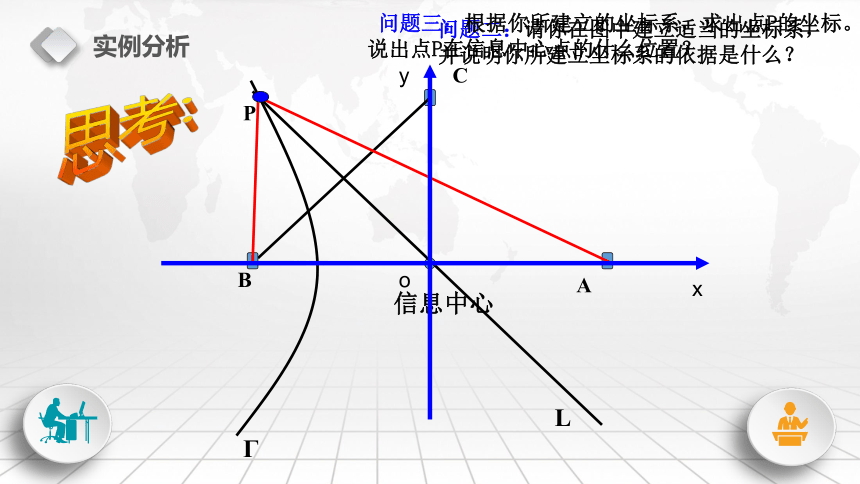
问题一:从点的轨迹角度分析点P在什么样的曲线上?互动中领悟ABCP实例分析PBCAΓ信息中心L思考:问题二:请你在图中建立适当的坐标系,
并说明你所建立坐标系的依据是什么? 问题三:根据你所建立的坐标系,求出点P的坐标。
说出点P在信息中心点的什么位置?
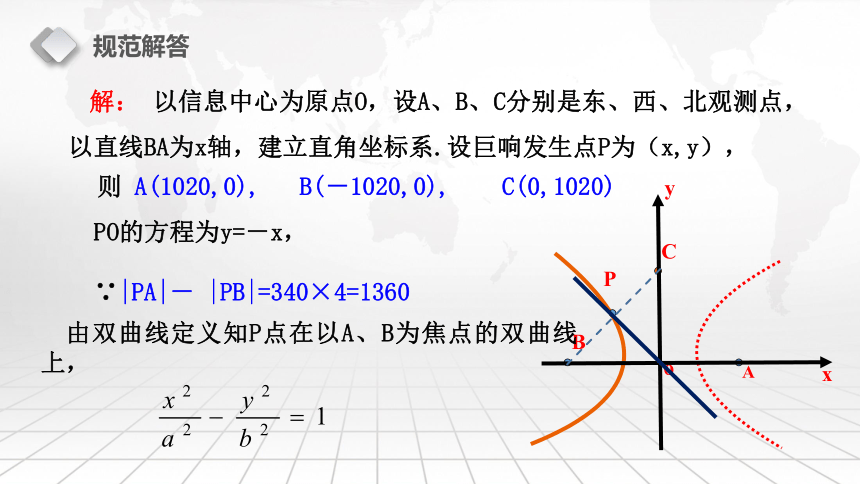
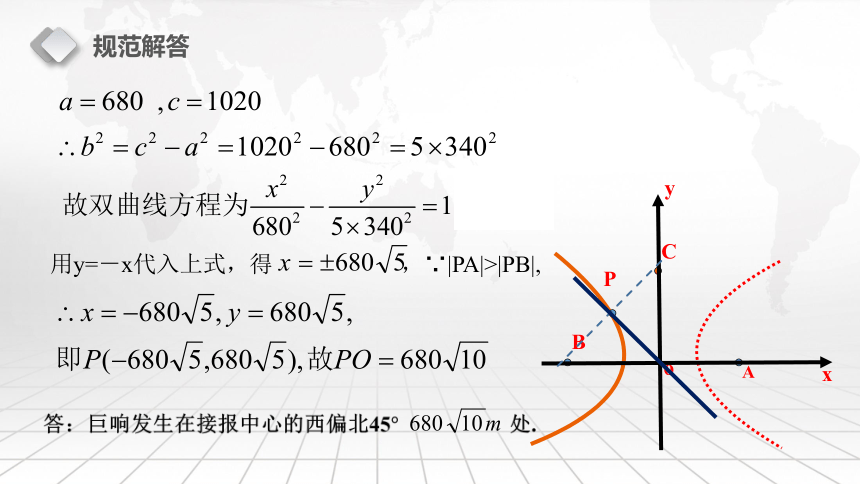
规范解答 解: 以信息中心为原点O,设A、B、C分别是东、西、北观测点,以直线BA为x轴,建立直角坐标系.设巨响发生点P为(x,y), PO的方程为y=-x,
∵|PA|- |PB|=340×4=1360则 A(1020,0), B(-1020,0), C(0,1020) 由双曲线定义知P点在以A、B为焦点的双曲线上,规范解答用y=-x代入上式,得 ,∵|PA|>|PB|,?1建立适当的
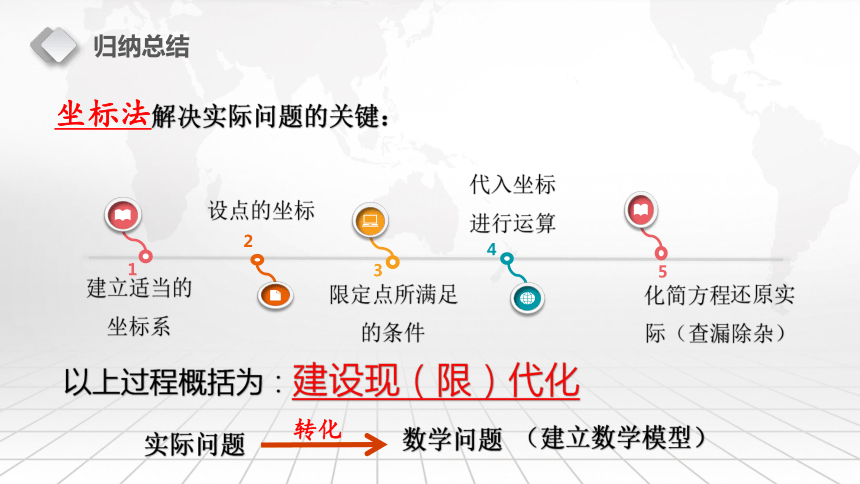
坐标系234限定点所满足
的条件设点的坐标代入坐标
进行运算归纳总结化简方程还原实际(查漏除杂)坐标法解决实际问题的关键:以上过程概括为:建设现(限)代化实际问题数学问题转化(建立数学模型)1典例分析O 以△ABC的顶点A为原点O,
边AB所在的直线x轴,建立直角
坐标系,由已知,点A、B、F的
坐标分别为A ( 0, 0 ) , B ( c ,0 ) , F ( ,0 ).解:典例分析因此,BE与CF互相垂直。Oyx0据几何特点选择归纳总结比较不同的直角坐标系下解决问题的过程,建立直角坐标系应注意什么问题?探究新知怎样由正弦曲线y=sinx得到曲线y=sin2x?怎样由正弦曲线y=sinx得到曲线y=3sinx?怎样由正弦曲线y=sinx得到曲线y=3sin2x?探究新知(1)怎样由正弦曲线y=sinx得到曲线y=sin2x?O?2?y=sinxy=sin2xyx横坐标缩短到原来的一半纵坐标不变1-1探究新知(2)怎样由正弦曲线y=sinx得到曲线y=3sinx?O?2?y=sinxy=3sinxyx-1123-2-3横坐标不变纵坐标伸长为原来的3倍探究新知(3)怎样由正弦曲线y=sinx得到曲线y=3sin2x?O?2?y=sinxy=3sin2xyx-3-2-1321纵坐标伸长为原来的3倍横坐标缩短为原来的一半的作用下,点P(x,y)对应到点 ,称 为平面直角坐标系中的坐标伸缩变换。、设P(x,y)是平面直角坐标系中任意一点,在变换抽象定义定 义注 意(1)
(2)把图形看成点的运动轨迹,平面图形的伸缩变换可以用坐标伸缩变换得到;
(3)在伸缩变换下,平面直角坐标系不变,在同一直角坐标系下进行伸缩变换。
辨析定义B-42(2,6)(-4,-3)抢答在直角坐标系中,求下列方程所对应的图形经过伸缩变换后的图形。2运用中提升小试牛刀在伸缩变换下,直线仍然变成直线,
而圆可以变成圆或椭圆。
在伸缩变换下,椭圆可以变成圆、
椭圆。
在伸缩变换下,抛物线变成抛物线,
双曲线变成双曲线。归纳总结学 有
所 获01变式乘胜追击答案:答案:02反思中收获凯旋归来话收获
对自己说,你有什么收获?
对老师说,你有什么疑惑?
对同学说,你有什么温馨提示?
121一种工具:平面直角坐标系一种解题方法:坐标法两个思想:转化思想,数形结合思想盘点收获121一种变换:坐标伸缩变换一种探究方法:由特殊到一般(归纳法)两个思想:转化思想,数形结合思想盘点收获02D达标检测A
问题一:从点的轨迹角度分析点P在什么样的曲线上?互动中领悟ABCP实例分析PBCAΓ信息中心L思考:问题二:请你在图中建立适当的坐标系,
并说明你所建立坐标系的依据是什么? 问题三:根据你所建立的坐标系,求出点P的坐标。
说出点P在信息中心点的什么位置?
规范解答 解: 以信息中心为原点O,设A、B、C分别是东、西、北观测点,以直线BA为x轴,建立直角坐标系.设巨响发生点P为(x,y), PO的方程为y=-x,
∵|PA|- |PB|=340×4=1360则 A(1020,0), B(-1020,0), C(0,1020) 由双曲线定义知P点在以A、B为焦点的双曲线上,规范解答用y=-x代入上式,得 ,∵|PA|>|PB|,?1建立适当的
坐标系234限定点所满足
的条件设点的坐标代入坐标
进行运算归纳总结化简方程还原实际(查漏除杂)坐标法解决实际问题的关键:以上过程概括为:建设现(限)代化实际问题数学问题转化(建立数学模型)1典例分析O 以△ABC的顶点A为原点O,
边AB所在的直线x轴,建立直角
坐标系,由已知,点A、B、F的
坐标分别为A ( 0, 0 ) , B ( c ,0 ) , F ( ,0 ).解:典例分析因此,BE与CF互相垂直。Oyx0据几何特点选择归纳总结比较不同的直角坐标系下解决问题的过程,建立直角坐标系应注意什么问题?探究新知怎样由正弦曲线y=sinx得到曲线y=sin2x?怎样由正弦曲线y=sinx得到曲线y=3sinx?怎样由正弦曲线y=sinx得到曲线y=3sin2x?探究新知(1)怎样由正弦曲线y=sinx得到曲线y=sin2x?O?2?y=sinxy=sin2xyx横坐标缩短到原来的一半纵坐标不变1-1探究新知(2)怎样由正弦曲线y=sinx得到曲线y=3sinx?O?2?y=sinxy=3sinxyx-1123-2-3横坐标不变纵坐标伸长为原来的3倍探究新知(3)怎样由正弦曲线y=sinx得到曲线y=3sin2x?O?2?y=sinxy=3sin2xyx-3-2-1321纵坐标伸长为原来的3倍横坐标缩短为原来的一半的作用下,点P(x,y)对应到点 ,称 为平面直角坐标系中的坐标伸缩变换。、设P(x,y)是平面直角坐标系中任意一点,在变换抽象定义定 义注 意(1)
(2)把图形看成点的运动轨迹,平面图形的伸缩变换可以用坐标伸缩变换得到;
(3)在伸缩变换下,平面直角坐标系不变,在同一直角坐标系下进行伸缩变换。
辨析定义B-42(2,6)(-4,-3)抢答在直角坐标系中,求下列方程所对应的图形经过伸缩变换后的图形。2运用中提升小试牛刀在伸缩变换下,直线仍然变成直线,
而圆可以变成圆或椭圆。
在伸缩变换下,椭圆可以变成圆、
椭圆。
在伸缩变换下,抛物线变成抛物线,
双曲线变成双曲线。归纳总结学 有
所 获01变式乘胜追击答案:答案:02反思中收获凯旋归来话收获
对自己说,你有什么收获?
对老师说,你有什么疑惑?
对同学说,你有什么温馨提示?
121一种工具:平面直角坐标系一种解题方法:坐标法两个思想:转化思想,数形结合思想盘点收获121一种变换:坐标伸缩变换一种探究方法:由特殊到一般(归纳法)两个思想:转化思想,数形结合思想盘点收获02D达标检测A
