6.2.2测量 整理与复习 课件(50张PPT)
文档属性
| 名称 | 6.2.2测量 整理与复习 课件(50张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 21:46:58 | ||
图片预览







文档简介
课件50张PPT。江苏省电化教育馆制作解决问题的策略
——转化 这种策略在我们的数学学习中有哪些应用的,它又能给我们带来什么样的启示,这节课老师将和大家一起探索和感受。 回忆:在小学阶段,我们学过哪些平面图形?哪些立体图形? 在学习推导这些图形的面积和体积时,我们是如何利用转化策略的?你们还能想起来吗?想……
下面请同学们跟着老师的镜头一起追溯曾经的画面……
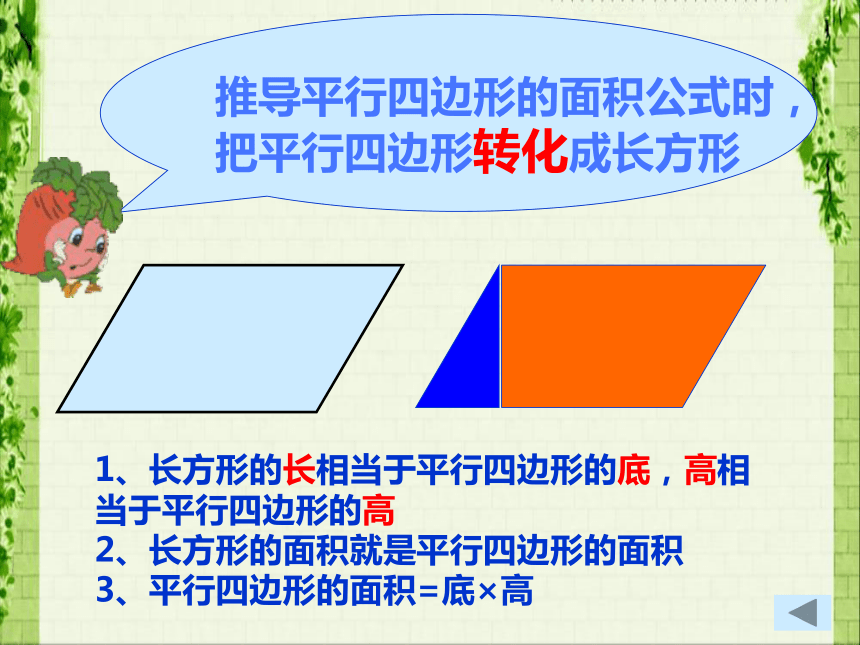
推导平行四边形的面积公式时,把平行四边形转化成长方形1、长方形的长相当于平行四边形的底,高相当于平行四边形的高
2、长方形的面积就是平行四边形的面积
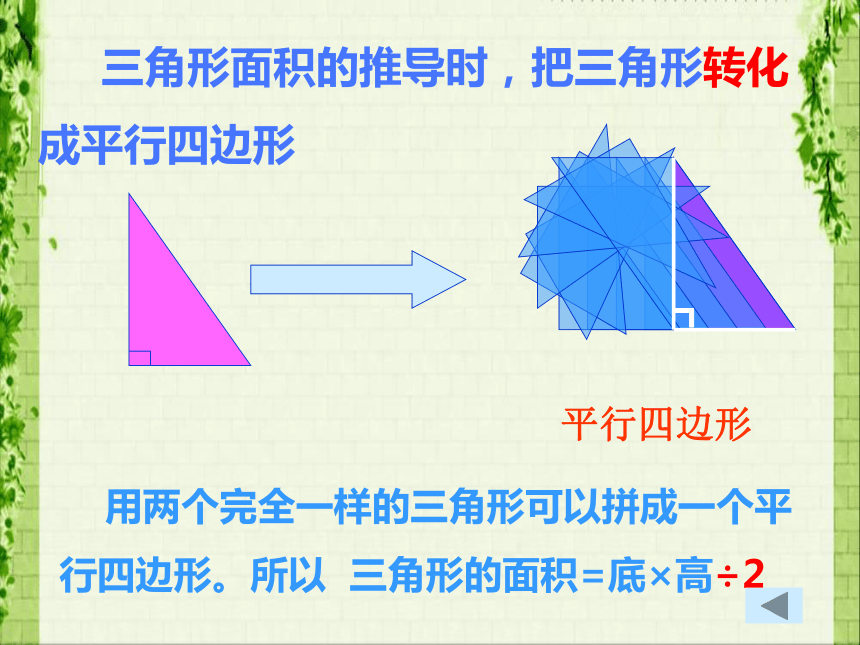
3、平行四边形的面积=底×高 三角形面积的推导时,把三角形转化成平行四边形平行四边形 用两个完全一样的三角形可以拼成一个平行四边形。所以 三角形的面积=底×高÷2两个 梯形完全一样的两个完全一样的梯形可以拼成的平行四边形的。
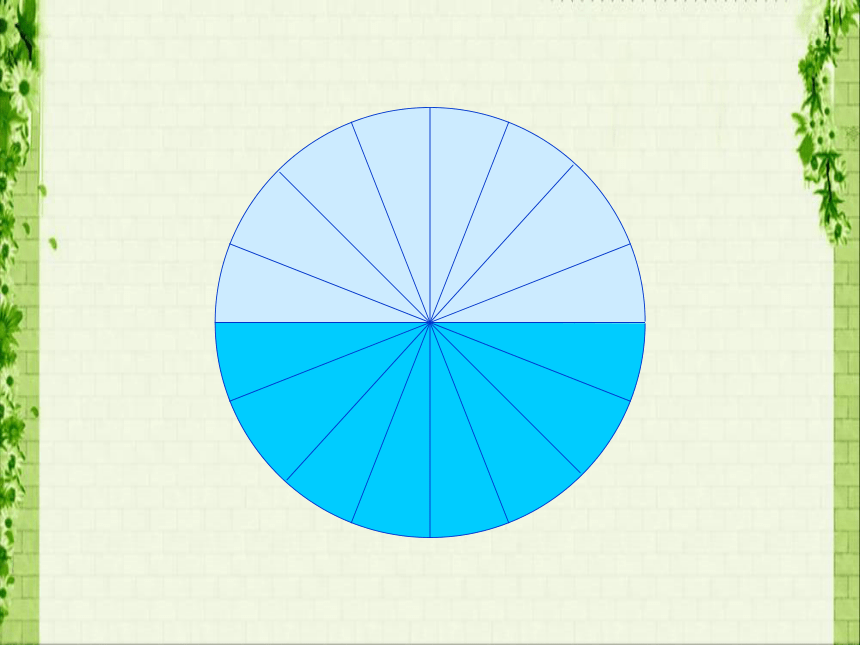
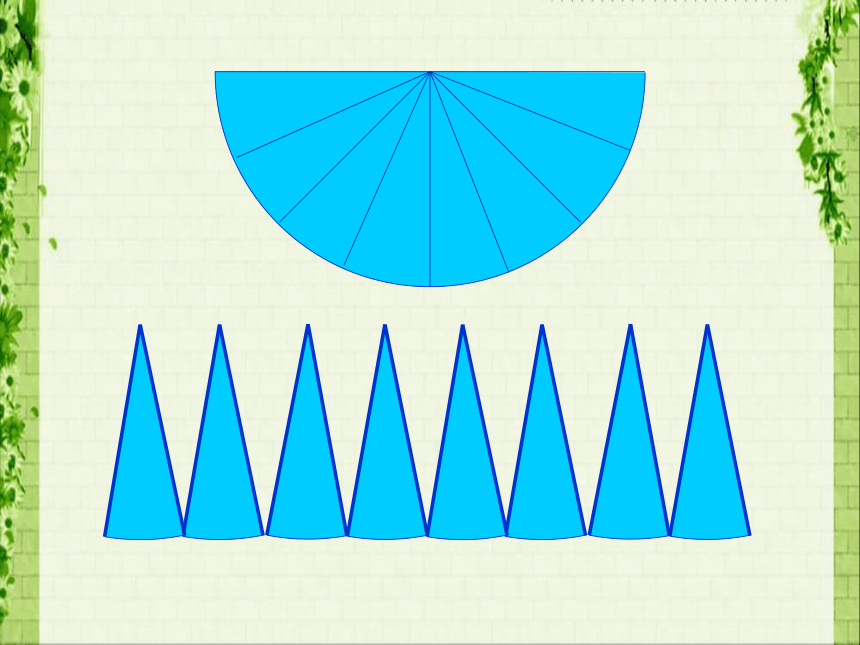
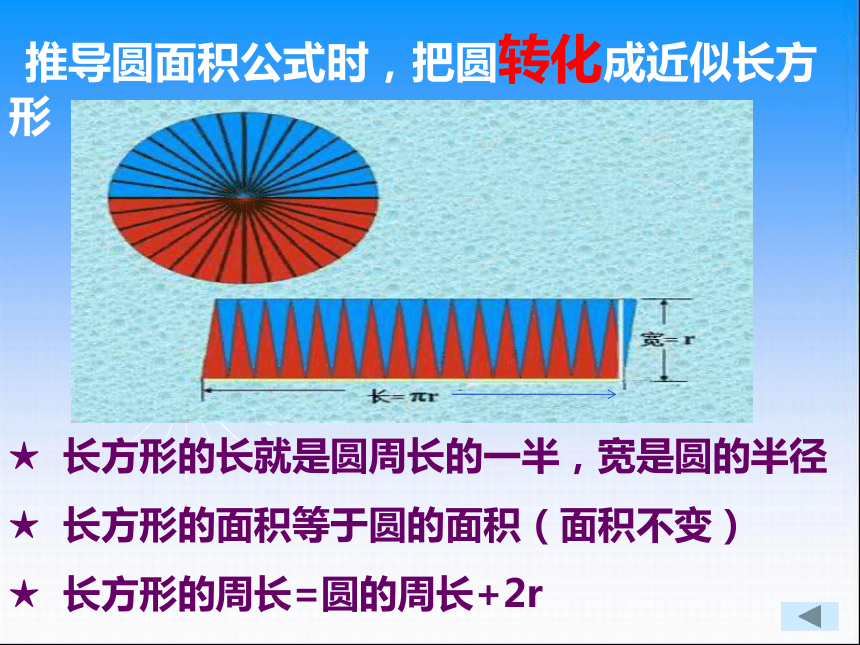
梯形的面积=(上底+下底)×高÷2 推导圆面积公式时,把圆转化成近似长方形★ 长方形的长就是圆周长的一半,宽是圆的半径
★ 长方形的面积等于圆的面积(面积不变)
★ 长方形的周长=圆的周长+2r 圆 柱 的 体 积推导圆柱体积公式时,把圆柱转化成长方体。1、 长方体的底面积就是圆的面积,长方体的高就是圆柱的高。
2、长方体的体积等于圆柱的体积(体积不变)
3、长方体的表面积比圆柱的表面积增加了2rh
4、正方体、长方体、圆柱体的体积都可以用底面积×高来计算
等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的圆锥的体积是圆柱的三分之一图 形 的 转 化新知旧知转化过关斩将 亲爱的小伙伴们,检验我们成果的时候到了,你准备好了吗?让我们一起嗨起来吧……第一关:明辨是非
1、圆锥的体积等于圆柱的三分之一 ( )
2、等底等高的正方体、长方体、圆柱和圆锥的体积相等 ( )
3、两个面积相等的三角形能拼成一个平行四边形 形 ( )
4、如果圆锥的体积是圆柱的三分之一,那么它们一定等底等高 ( )1、一个长方体和一个圆柱体的底面积和高相等,则它们的体积比是( )
2、下面两个图形的周长相比较( )
第二关:我会填第三关:求阴影部分的面积2厘米2厘米2厘米2厘米2厘米第三关:求阴影部分的面积2厘米2厘米第三关:求阴影部分的面积2厘米2厘米第三关:求阴影部分的面积2厘米2厘米第三关:求阴影部分的面积2厘米2厘米第三关:求阴影部分的面积第三关:求红色阴影部分的面积 4厘米6厘米第三关 :求阴影部分的面积第三关:阴影部分的面积第四关:
圆的面积等于长方形的面积,圆的周长是31.4厘米,求阴影部分的面积
第五关:
一个圆柱形容器的底面半径是10厘米,把一个铁球从这个容器的水中取出,水面下降了4厘米,求这个铁球的体积是多少立方厘米?
用转化的策略解决问题学习数学讲策略,数学策略真不少
复杂转化为简单,陌生转化为熟悉
抽象转化为具体,未知转化为已知
转化策略在身边,处处留心记心间 通过今天的学习,同学们一定有很多的感想和收获 从前,有位老太太有两个儿子,大儿子是卖雨伞的,小儿子是卖西瓜的。于是,老太太成天忧心忡忡,每逢下雨天,她担心西瓜卖不掉;天晴时,又担心雨伞卖不出去。日子过得非常忧郁。 后来,一位聪明人告诉她:“老太太,你真是好福气!下雨天,你大儿子家生意兴隆;天晴时,你小儿子家顾客盈门,哪一天都有好消息呀!”这位老太太一想,立刻笑逐颜开了。 所以有些时候,换个角度去想问题,你会发现真的很不一样!其实自己快乐与否,重在心态。只要你用乐观的心态去面对,无论任何事情,都会是快乐的!
——转化 这种策略在我们的数学学习中有哪些应用的,它又能给我们带来什么样的启示,这节课老师将和大家一起探索和感受。 回忆:在小学阶段,我们学过哪些平面图形?哪些立体图形? 在学习推导这些图形的面积和体积时,我们是如何利用转化策略的?你们还能想起来吗?想……
下面请同学们跟着老师的镜头一起追溯曾经的画面……
推导平行四边形的面积公式时,把平行四边形转化成长方形1、长方形的长相当于平行四边形的底,高相当于平行四边形的高
2、长方形的面积就是平行四边形的面积
3、平行四边形的面积=底×高 三角形面积的推导时,把三角形转化成平行四边形平行四边形 用两个完全一样的三角形可以拼成一个平行四边形。所以 三角形的面积=底×高÷2两个 梯形完全一样的两个完全一样的梯形可以拼成的平行四边形的。
梯形的面积=(上底+下底)×高÷2 推导圆面积公式时,把圆转化成近似长方形★ 长方形的长就是圆周长的一半,宽是圆的半径
★ 长方形的面积等于圆的面积(面积不变)
★ 长方形的周长=圆的周长+2r 圆 柱 的 体 积推导圆柱体积公式时,把圆柱转化成长方体。1、 长方体的底面积就是圆的面积,长方体的高就是圆柱的高。
2、长方体的体积等于圆柱的体积(体积不变)
3、长方体的表面积比圆柱的表面积增加了2rh
4、正方体、长方体、圆柱体的体积都可以用底面积×高来计算
等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的:等底等高的圆锥的体积是圆柱的三分之一图 形 的 转 化新知旧知转化过关斩将 亲爱的小伙伴们,检验我们成果的时候到了,你准备好了吗?让我们一起嗨起来吧……第一关:明辨是非
1、圆锥的体积等于圆柱的三分之一 ( )
2、等底等高的正方体、长方体、圆柱和圆锥的体积相等 ( )
3、两个面积相等的三角形能拼成一个平行四边形 形 ( )
4、如果圆锥的体积是圆柱的三分之一,那么它们一定等底等高 ( )1、一个长方体和一个圆柱体的底面积和高相等,则它们的体积比是( )
2、下面两个图形的周长相比较( )
第二关:我会填第三关:求阴影部分的面积2厘米2厘米2厘米2厘米2厘米第三关:求阴影部分的面积2厘米2厘米第三关:求阴影部分的面积2厘米2厘米第三关:求阴影部分的面积2厘米2厘米第三关:求阴影部分的面积2厘米2厘米第三关:求阴影部分的面积第三关:求红色阴影部分的面积 4厘米6厘米第三关 :求阴影部分的面积第三关:阴影部分的面积第四关:
圆的面积等于长方形的面积,圆的周长是31.4厘米,求阴影部分的面积
第五关:
一个圆柱形容器的底面半径是10厘米,把一个铁球从这个容器的水中取出,水面下降了4厘米,求这个铁球的体积是多少立方厘米?
用转化的策略解决问题学习数学讲策略,数学策略真不少
复杂转化为简单,陌生转化为熟悉
抽象转化为具体,未知转化为已知
转化策略在身边,处处留心记心间 通过今天的学习,同学们一定有很多的感想和收获 从前,有位老太太有两个儿子,大儿子是卖雨伞的,小儿子是卖西瓜的。于是,老太太成天忧心忡忡,每逢下雨天,她担心西瓜卖不掉;天晴时,又担心雨伞卖不出去。日子过得非常忧郁。 后来,一位聪明人告诉她:“老太太,你真是好福气!下雨天,你大儿子家生意兴隆;天晴时,你小儿子家顾客盈门,哪一天都有好消息呀!”这位老太太一想,立刻笑逐颜开了。 所以有些时候,换个角度去想问题,你会发现真的很不一样!其实自己快乐与否,重在心态。只要你用乐观的心态去面对,无论任何事情,都会是快乐的!
