高二数学人教A版选修2-2 1.5.1 曲边梯形的面积(共26张ppt)
文档属性
| 名称 | 高二数学人教A版选修2-2 1.5.1 曲边梯形的面积(共26张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 00:00:00 | ||
图片预览



文档简介
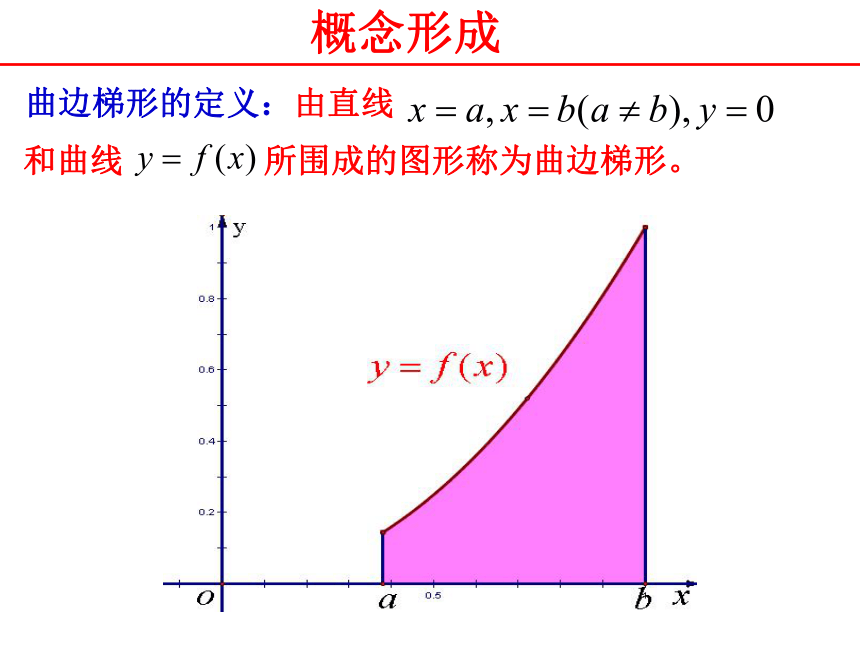
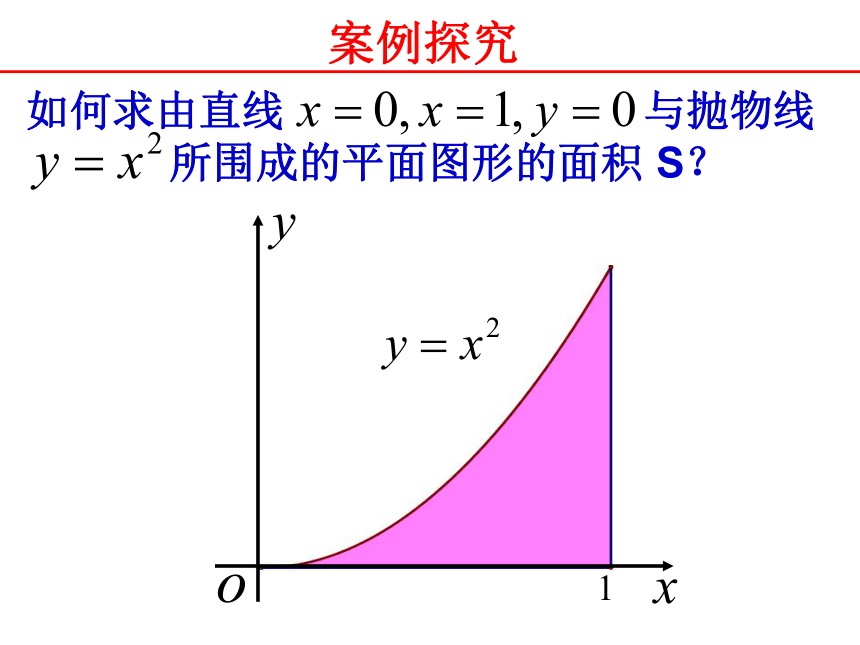
课件26张PPT。曲边梯形的面积高二数学人教A版选修2-1 情境创设 金门大桥 (美国)和曲线 所围成的图形称为曲边梯形。 曲边梯形的定义:由直线 概念形成 案例探究 如何求由直线 与抛物线
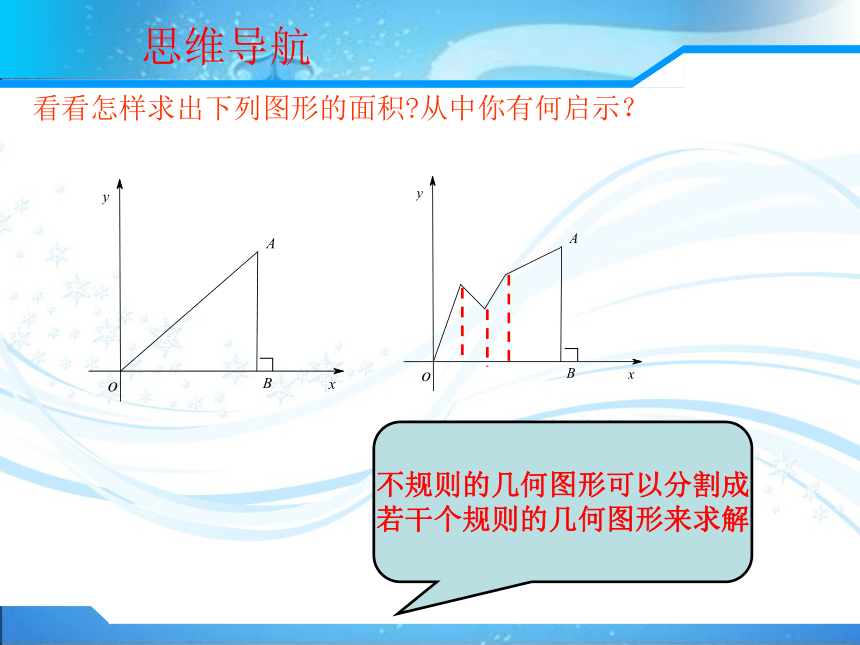
所围成的平面图形的面积 S?看看怎样求出下列图形的面积?从中你有何启示?∟∟思维导航不规则的几何图形可以分割成
若干个规则的几何图形来求解思维导航 割之弥细,
所失弥少,
割之又割,
以至于不可割,
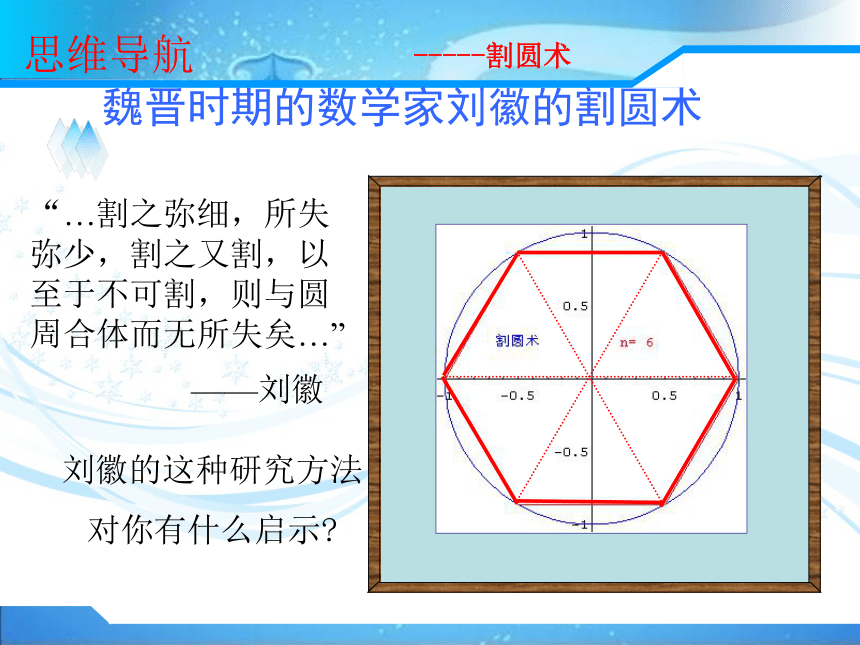
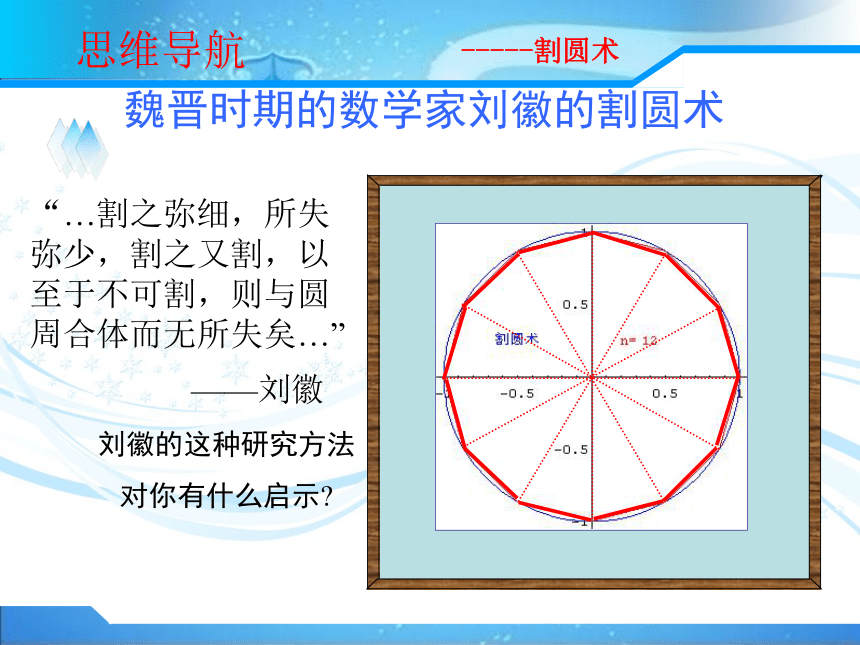
则与圆周合体而无所失矣.-----割圆术 魏晋时期的数学家刘徽的割圆术“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”——刘徽刘徽的这种研究方法
对你有什么启示?思维导航-----割圆术魏晋时期的数学家刘徽的割圆术“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”——刘徽刘徽的这种研究方法
对你有什么启示?
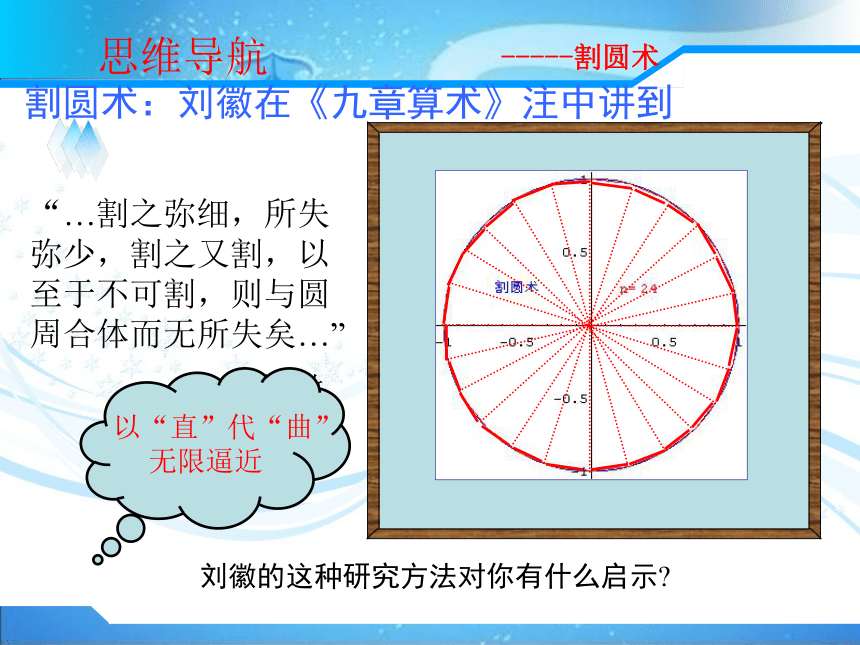
思维导航-----割圆术“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”割圆术:刘徽在《九章算术》注中讲到——刘徽刘徽的这种研究方法对你有什么启示?
-----割圆术思维导航 以“直”代“曲”
无限逼近案例探究 如何求由直线 与抛物线
所围成的平面图形的面积 S?思考1:怎样“以直代曲”?
能整体以“直”代“曲吗?
思考2:怎样分割最简单?
1、分割将曲边梯形分割为等高的小曲边梯形这样[0,1]区间分成n个小区间:对应的小曲边梯形面积为△Si把底边[0,1]分成n等份, 在每个分点作底边的垂线,案例探究 2、近似代替(以直代曲)方案.方案..方案…方案….案例探究 思考3:对每个小曲边梯形
如何“以直代曲”?
怎样使各个结果更接近真实值?深入思考通过动画演示我们可以看出,n越大,区间分的越细,各个结果就越接近真实值。为此,我们让n无限变大,这就是一个求极限的过程。深入思考方案一 方案二 方案三 第四步:取极限
(1)在分割时一定要等分吗?不等分影响结果吗?
(2)在近似代替时用小区间内任一点处的函数值影响结果吗 ?
(3)总结一般曲边梯形面积的表达式?两个结论1.在分割时,不管采用等分与不等分,结果一样。 2. 在近似代替时,用小区间内任 一点处的函数值作为近似值,结果也是一样的。归纳概括 一般曲边梯形的面积的表达式 以上计算曲边三角形面积的过程可以用流程图表示:即时小结联系生活联系生活联系生活学以致用拓展弹簧在拉伸过程中,力与伸长量成正比,即力F=kx(k是常数,x 是伸长量),求弹簧从平衡位置拉长b所做的功W。求一个具体曲边梯形的面积 方案一、方案二、方案三 分割、近似代替、求和、求极限 “以直代曲”和“无限逼近”思想 课堂小结 课堂练习:1.B 2.D 3.C 4._1__,_[3,4]_.5.26有位成功人士曾说过:“做事业的过程就是在求解一条曲线长度的过程。每一件实实在在的小事就是组成事业曲线的直线段。”想想我们的学习过程、追求理想的过程又何尝不是这样?希望大家能用微积分的思想去学习、去做事!
所围成的平面图形的面积 S?看看怎样求出下列图形的面积?从中你有何启示?∟∟思维导航不规则的几何图形可以分割成
若干个规则的几何图形来求解思维导航 割之弥细,
所失弥少,
割之又割,
以至于不可割,
则与圆周合体而无所失矣.-----割圆术 魏晋时期的数学家刘徽的割圆术“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”——刘徽刘徽的这种研究方法
对你有什么启示?思维导航-----割圆术魏晋时期的数学家刘徽的割圆术“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”——刘徽刘徽的这种研究方法
对你有什么启示?
思维导航-----割圆术“…割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣…”割圆术:刘徽在《九章算术》注中讲到——刘徽刘徽的这种研究方法对你有什么启示?
-----割圆术思维导航 以“直”代“曲”
无限逼近案例探究 如何求由直线 与抛物线
所围成的平面图形的面积 S?思考1:怎样“以直代曲”?
能整体以“直”代“曲吗?
思考2:怎样分割最简单?
1、分割将曲边梯形分割为等高的小曲边梯形这样[0,1]区间分成n个小区间:对应的小曲边梯形面积为△Si把底边[0,1]分成n等份, 在每个分点作底边的垂线,案例探究 2、近似代替(以直代曲)方案.方案..方案…方案….案例探究 思考3:对每个小曲边梯形
如何“以直代曲”?
怎样使各个结果更接近真实值?深入思考通过动画演示我们可以看出,n越大,区间分的越细,各个结果就越接近真实值。为此,我们让n无限变大,这就是一个求极限的过程。深入思考方案一 方案二 方案三 第四步:取极限
(1)在分割时一定要等分吗?不等分影响结果吗?
(2)在近似代替时用小区间内任一点处的函数值影响结果吗 ?
(3)总结一般曲边梯形面积的表达式?两个结论1.在分割时,不管采用等分与不等分,结果一样。 2. 在近似代替时,用小区间内任 一点处的函数值作为近似值,结果也是一样的。归纳概括 一般曲边梯形的面积的表达式 以上计算曲边三角形面积的过程可以用流程图表示:即时小结联系生活联系生活联系生活学以致用拓展弹簧在拉伸过程中,力与伸长量成正比,即力F=kx(k是常数,x 是伸长量),求弹簧从平衡位置拉长b所做的功W。求一个具体曲边梯形的面积 方案一、方案二、方案三 分割、近似代替、求和、求极限 “以直代曲”和“无限逼近”思想 课堂小结 课堂练习:1.B 2.D 3.C 4._1__,_[3,4]_.5.26有位成功人士曾说过:“做事业的过程就是在求解一条曲线长度的过程。每一件实实在在的小事就是组成事业曲线的直线段。”想想我们的学习过程、追求理想的过程又何尝不是这样?希望大家能用微积分的思想去学习、去做事!
