人教A版数学选修2—2 3.1.1 数系的扩充和复数的概念(共17张ppt)
文档属性
| 名称 | 人教A版数学选修2—2 3.1.1 数系的扩充和复数的概念(共17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 00:00:00 | ||
图片预览




文档简介
课件17张PPT。 3.1.1数系的扩充和复数的概念阅读小资料-回忆数系扩充历程 远古的人类,为了统计捕获的野兽和采集的野果,历经漫长的岁月,创造了自然数。自然数是现实世界最基本的数量,是全部数学的发源地。自然数的加法与乘法满足交换律、结合律及分配律。
随着历史的发展,为了公平分配物质印度人引进了分数,但分数的确切定义,科学表示及分数算法,都是中国最早提出的。分数运算也满足加法与乘法的运算律。
随后为了表示具有相反意义的量,负数的概念就出现了,我国是认识正负数最早的国家,《九章算术》中就有了正负数的记载。负数概念引进后,就把数集扩充到有理数集Q,运算法则同样适用。
公元前几百年,希腊人发现边长为1的正方形和正五边形对角线的长都不是分数,从此人们知道了世间还存在另一类数无理数。有理数集与无理数集合并在一起就构成实数集。
数系的每一次扩充,都解决了在原有数集中某种运算不能实施的矛盾,原数集中的运算规则在新数集中得到了保留。
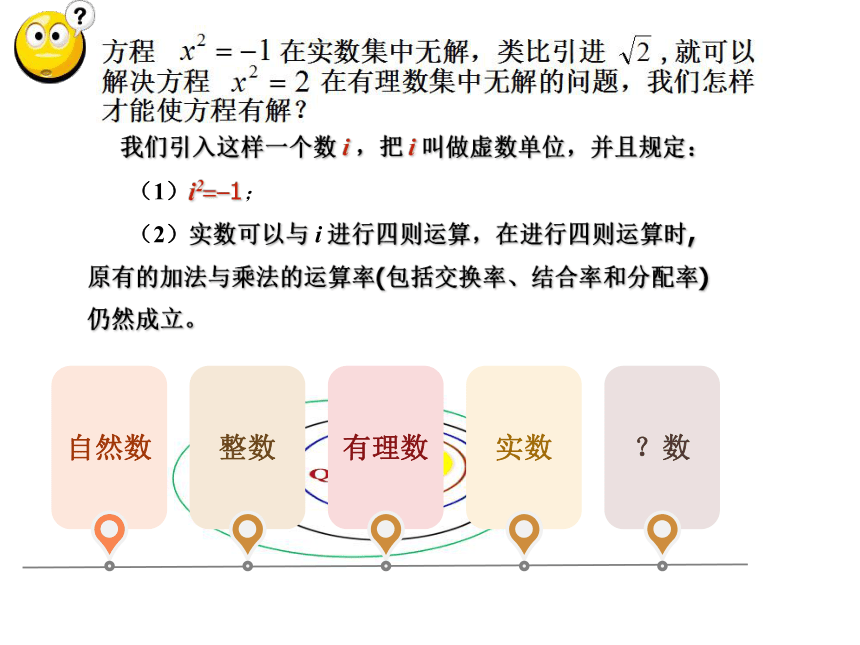
我们引入这样一个数 i ,把 i 叫做虚数单位,并且规定:
(1)i2??1;
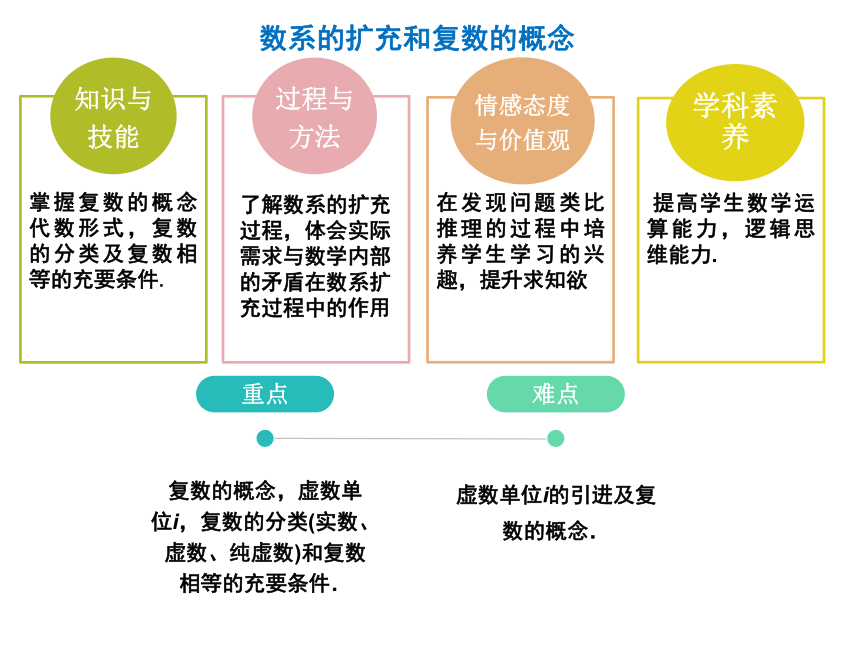
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算率(包括交换率、结合率和分配率)仍然成立。 数系的扩充和复数的概念掌握复数的概念代数形式,复数的分类及复数相等的充要条件.知识与技能了解数系的扩充过程,体会实际过程与方法在发现问题类比推理的过程中培养学生学习的兴趣,提升求知欲情感态度与价值观 提高学生数学运算能力,逻辑思维能力.
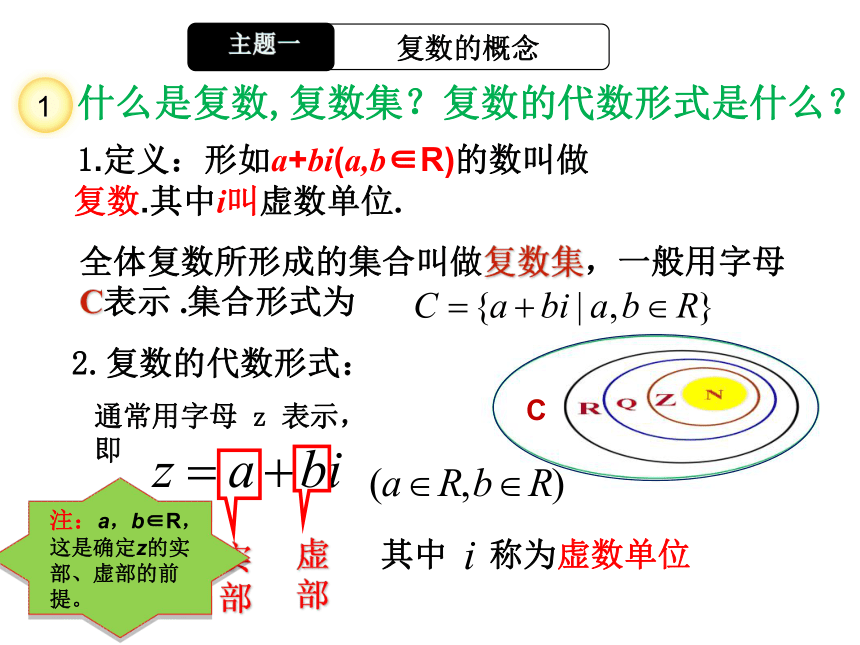
学科素养了解数系的扩充过程,体会实际需求与数学内部的矛盾在数系扩充过程中的作用 数系的扩充和复数的概念复数概念复数分类复数相等什么是复数,复数集?复数的代数形式是什么? 1.定义:形如a+bi(a,b∈R)的数叫做
复数.其中i叫虚数单位.全体复数所形成的集合叫做复数集,一般用字母C表示 .集合形式为2.复数的代数形式:通常用字母 z 表示,即其中 称为虚数单位1C复数集、实数集、虚数集、纯虚集
之间的关系?2复数的分类?特别地,a+bi=0 (a,b∈R)当且仅当a=b=0.a+bi=c+di (a,b,c,d∈R)当且仅当a=c且b=d.怎样定义两个复数相等?
3规定:如果两个复数的实部和虚部分别相等,我们就说这两个复数相等.复数相等的充要条件是:实部与虚部分别对应相等。4 3+2i与2能比较大小吗?两个复数可以比较大小吗?
【练一练】12+i2= ,是一个复数吗?注①研究一个复数在什么情况下是实数、虚数或纯虚数,首先保证复数的实部和虚部有意义.本题分母不为零的条件容易忽略.②纯虚数要求实部为零的条件也易考虑不周.通关检测复 数 z = a + bi(a,b∈R)复数的分类当b=0时z为实数;当b?0时z为虚数(此时,当a =0时z为纯虚数).复数的相等a+bi=c+di(a, b,c,d?R) 回顾总结
随着历史的发展,为了公平分配物质印度人引进了分数,但分数的确切定义,科学表示及分数算法,都是中国最早提出的。分数运算也满足加法与乘法的运算律。
随后为了表示具有相反意义的量,负数的概念就出现了,我国是认识正负数最早的国家,《九章算术》中就有了正负数的记载。负数概念引进后,就把数集扩充到有理数集Q,运算法则同样适用。
公元前几百年,希腊人发现边长为1的正方形和正五边形对角线的长都不是分数,从此人们知道了世间还存在另一类数无理数。有理数集与无理数集合并在一起就构成实数集。
数系的每一次扩充,都解决了在原有数集中某种运算不能实施的矛盾,原数集中的运算规则在新数集中得到了保留。
我们引入这样一个数 i ,把 i 叫做虚数单位,并且规定:
(1)i2??1;
(2)实数可以与 i 进行四则运算,在进行四则运算时,原有的加法与乘法的运算率(包括交换率、结合率和分配率)仍然成立。 数系的扩充和复数的概念掌握复数的概念代数形式,复数的分类及复数相等的充要条件.知识与技能了解数系的扩充过程,体会实际过程与方法在发现问题类比推理的过程中培养学生学习的兴趣,提升求知欲情感态度与价值观 提高学生数学运算能力,逻辑思维能力.
学科素养了解数系的扩充过程,体会实际需求与数学内部的矛盾在数系扩充过程中的作用 数系的扩充和复数的概念复数概念复数分类复数相等什么是复数,复数集?复数的代数形式是什么? 1.定义:形如a+bi(a,b∈R)的数叫做
复数.其中i叫虚数单位.全体复数所形成的集合叫做复数集,一般用字母C表示 .集合形式为2.复数的代数形式:通常用字母 z 表示,即其中 称为虚数单位1C复数集、实数集、虚数集、纯虚集
之间的关系?2复数的分类?特别地,a+bi=0 (a,b∈R)当且仅当a=b=0.a+bi=c+di (a,b,c,d∈R)当且仅当a=c且b=d.怎样定义两个复数相等?
3规定:如果两个复数的实部和虚部分别相等,我们就说这两个复数相等.复数相等的充要条件是:实部与虚部分别对应相等。4 3+2i与2能比较大小吗?两个复数可以比较大小吗?
【练一练】12+i2= ,是一个复数吗?注①研究一个复数在什么情况下是实数、虚数或纯虚数,首先保证复数的实部和虚部有意义.本题分母不为零的条件容易忽略.②纯虚数要求实部为零的条件也易考虑不周.通关检测复 数 z = a + bi(a,b∈R)复数的分类当b=0时z为实数;当b?0时z为虚数(此时,当a =0时z为纯虚数).复数的相等a+bi=c+di(a, b,c,d?R) 回顾总结
