人教A版数学选修2—2 1.3.1 函数的单调性与导数 课件(共27ppt)
文档属性
| 名称 | 人教A版数学选修2—2 1.3.1 函数的单调性与导数 课件(共27ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 19:54:05 | ||
图片预览





文档简介
课件27张PPT。都说一年有四季,但龙口 的天气比较强势,
谋杀了夏天,赶走了秋天,
留下一抹寒冬,不是热死就是冷死.
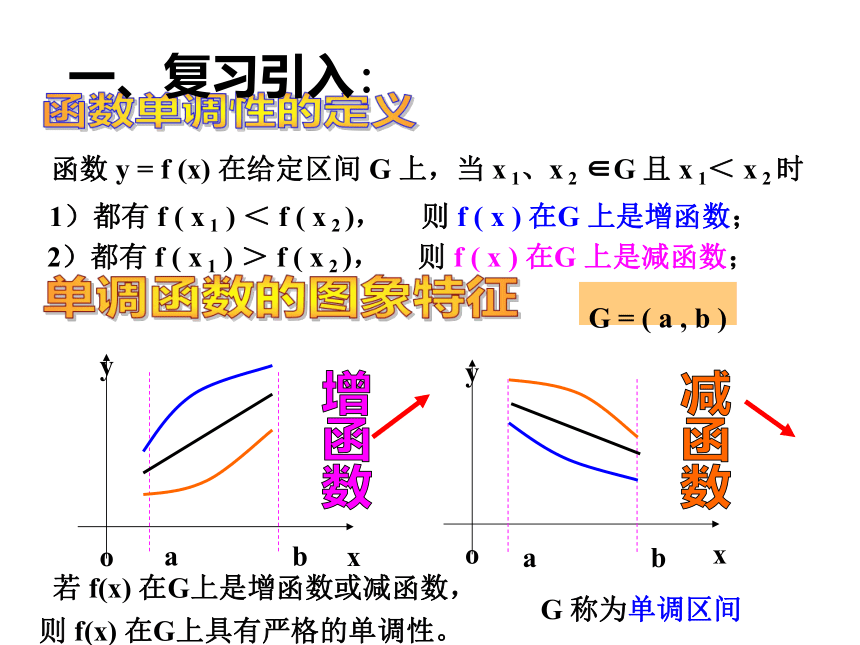
让你一天经历四季都不是神话函数 y = f (x) 在给定区间 G 上,当 x 1、x 2 ∈G 且 x 1< x 2 时函数单调性的定义单调函数的图象特征1)都有 f ( x 1 ) < f ( x 2 ),则 f ( x ) 在G 上是增函数;2)都有 f ( x 1 ) > f ( x 2 ),则 f ( x ) 在G 上是减函数;若 f(x) 在G上是增函数或减函数,增函数减函数则 f(x) 在G上具有严格的单调性。G 称为单调区间G = ( a , b )一、复习引入:引例、 已知函数y=2x3-6x2+7,
求证:这个函数在区间(0,2)上是单调递增的. (1)任取x1 ( 2 ) 作差f(x1)-f(x2)
(3) 变形
(4)判断符号
(5)下结论用定义法判断函数单调性的步骤:1.3.1 函数的单调性与导数普通高中课程标准实验教科书(人教A版选修2-2)1.正确理解利用导数判断函数的单调性的原理. (重点)
2.利用导数判断函数单调性.(难点)
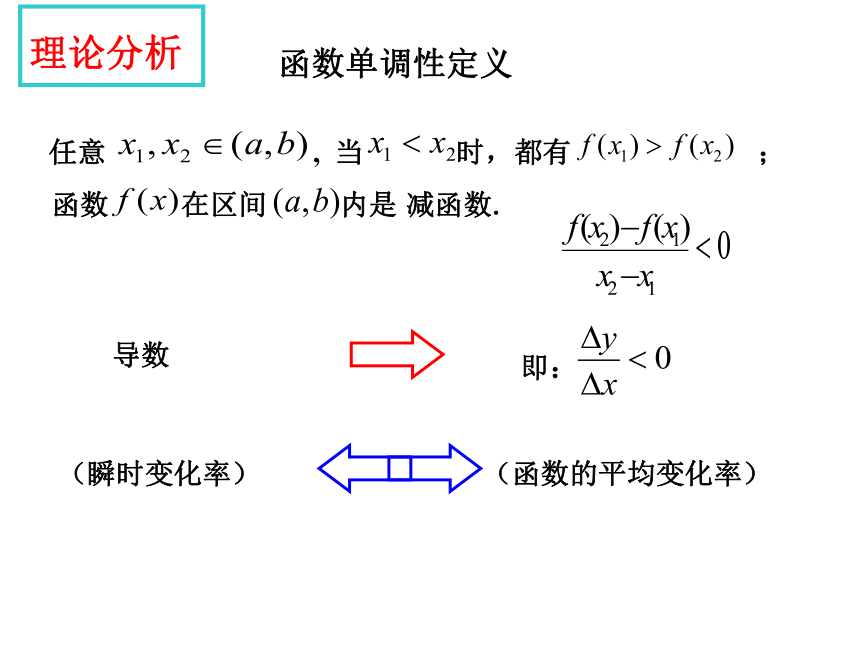
3.掌握利用导数判断函数单调性的方法.理论分析即: 函数单调性定义
函数 在区间 内是(函数的平均变化率)导数(瞬时变化率)理论分析即: 减函数.函数单调性定义
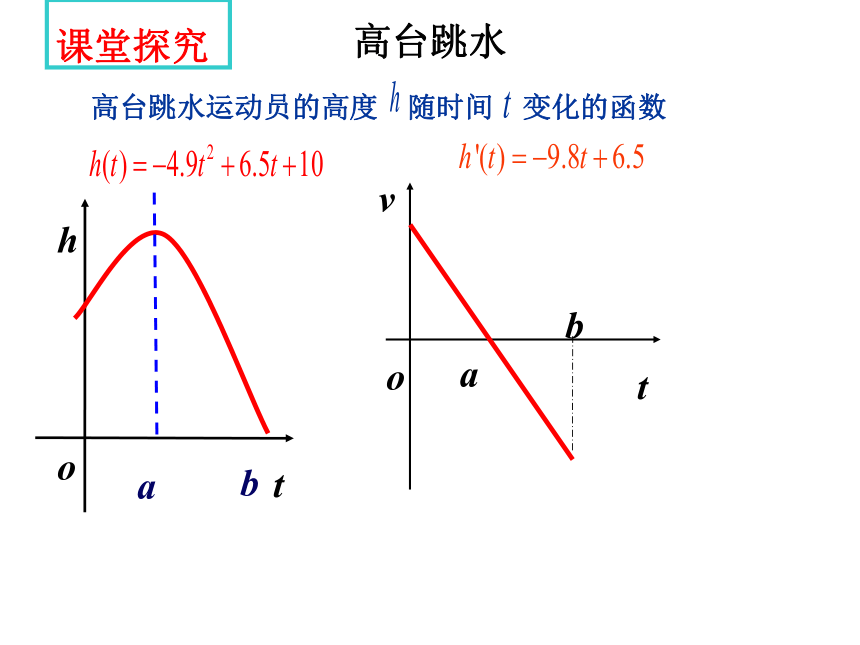
高台跳水课堂探究 高台跳水运动员的高度 随时间 变化的函数
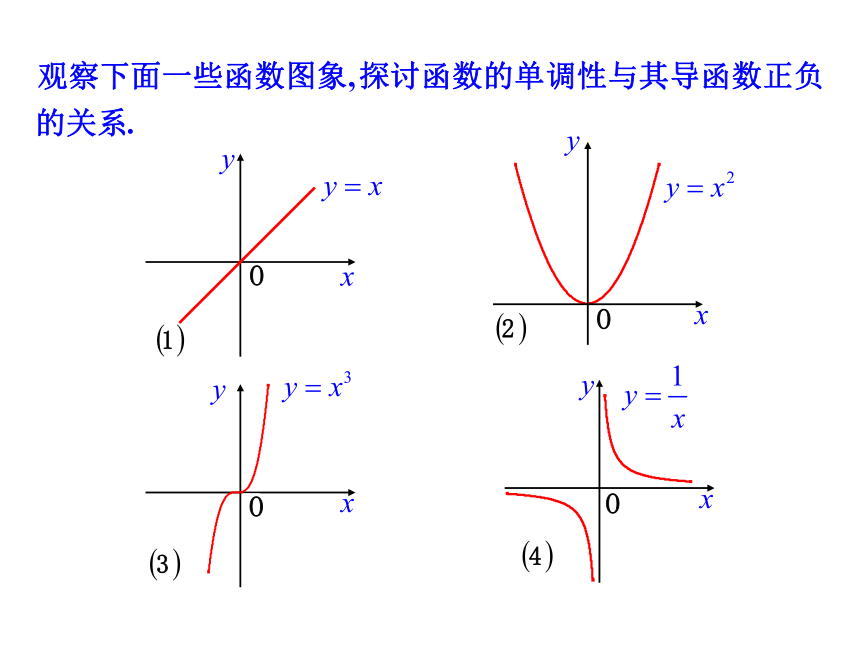
OOOO例1 已知导函数 的下列信息:当1 < x < 4 时,当 x > 4 , 或 x < 1时,当 x = 4 , 或 x = 1时,试画出函数f(x)图象的大致形状.题型一 原函数和导函数图象之间的关系 跟踪练习2 已知函数y=f(x)的图象如图所示,则函数y=f′(x)的图象可能是图中的题型二 利用导数求函数单调区间例2.判断函数 的单调性,并求出单调区间.注意定义域解:解:正确解法判断函数 的单调性,并求出单调区间.再次强调:研究函数先判断定义域;若有多个单调增(减)区间,用“,”或者“和”连接知识小结:一般地,函数y=f(x)在某个区间内:
如果 ,则 f(x)在该区间是增函数。
如果 ,则 f(x)在该区间是减函数。
f’(x)>0f’(x)<0导函数f’(x)的------与原函数f(x)的增减性有关正负根据导数确定函数的单调性步骤:1.确定函数f(x)的定义域.2.求出函数的导数.3.解不等式f′(x)>0,得函数单调增区间;
解不等式f′(x)<0,得函数单调减区间.例2 判断下列函数的单调性, 并求出单调区间:因此, 函数 在
上单调递增.如图(1)所示单调递减附加题: 1. 已知函数f(x)=ax3+3x2-x+1在(-∞,+∞)上是减函数,求实数a的取值范围.
2.若函数 在区间 单调递增,则k的取值范围是( )
A. B.
C. D.课堂小结过山车回归生活感悟:数学来源于生活 人生犹如过山车,站在人生的每个瞬间的点上,我们都能向上看,人生轨迹就会是持续上升趋势;相反,如果我们被负面情绪萦绕,我们就会走下坡路.
只要饱含正能量,脚踏实地走好每一步,相信我们的前途会一片光明!
体会数学
求证:这个函数在区间(0,2)上是单调递增的. (1)任取x1
(3) 变形
(4)判断符号
(5)下结论用定义法判断函数单调性的步骤:1.3.1 函数的单调性与导数普通高中课程标准实验教科书(人教A版选修2-2)1.正确理解利用导数判断函数的单调性的原理. (重点)
2.利用导数判断函数单调性.(难点)
3.掌握利用导数判断函数单调性的方法.理论分析即: 函数单调性定义
函数 在区间 内是(函数的平均变化率)导数(瞬时变化率)理论分析即: 减函数.函数单调性定义
高台跳水课堂探究 高台跳水运动员的高度 随时间 变化的函数
OOOO例1 已知导函数 的下列信息:当1 < x < 4 时,当 x > 4 , 或 x < 1时,当 x = 4 , 或 x = 1时,试画出函数f(x)图象的大致形状.题型一 原函数和导函数图象之间的关系 跟踪练习2 已知函数y=f(x)的图象如图所示,则函数y=f′(x)的图象可能是图中的题型二 利用导数求函数单调区间例2.判断函数 的单调性,并求出单调区间.注意定义域解:解:正确解法判断函数 的单调性,并求出单调区间.再次强调:研究函数先判断定义域;若有多个单调增(减)区间,用“,”或者“和”连接知识小结:一般地,函数y=f(x)在某个区间内:
如果 ,则 f(x)在该区间是增函数。
如果 ,则 f(x)在该区间是减函数。
f’(x)>0f’(x)<0导函数f’(x)的------与原函数f(x)的增减性有关正负根据导数确定函数的单调性步骤:1.确定函数f(x)的定义域.2.求出函数的导数.3.解不等式f′(x)>0,得函数单调增区间;
解不等式f′(x)<0,得函数单调减区间.例2 判断下列函数的单调性, 并求出单调区间:因此, 函数 在
上单调递增.如图(1)所示单调递减附加题: 1. 已知函数f(x)=ax3+3x2-x+1在(-∞,+∞)上是减函数,求实数a的取值范围.
2.若函数 在区间 单调递增,则k的取值范围是( )
A. B.
C. D.课堂小结过山车回归生活感悟:数学来源于生活 人生犹如过山车,站在人生的每个瞬间的点上,我们都能向上看,人生轨迹就会是持续上升趋势;相反,如果我们被负面情绪萦绕,我们就会走下坡路.
只要饱含正能量,脚踏实地走好每一步,相信我们的前途会一片光明!
体会数学
