人教A版数学选修2—3 1.2.2 组合(共16张ppt)
文档属性
| 名称 | 人教A版数学选修2—3 1.2.2 组合(共16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 591.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 00:00:00 | ||
图片预览





文档简介
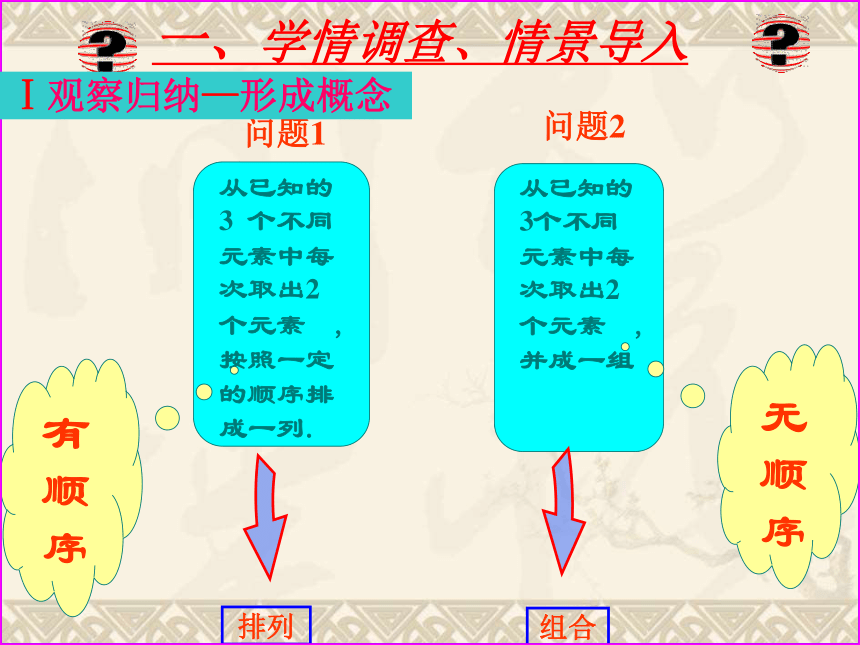
课件16张PPT。易水寒江雪敬奉1.2.2 组合一、学情调查、情景导入 A B C问题一:五一期间到青岛旅游,要从A、B、C、三处景色中选择两处,上午选1处,下午选一处,有多少种不同的旅游方案? 一、学情调查、情景导入 A B C问题二:五一期间到青岛旅游,要从A、B、C、三处景色中选择两处,有多少种不同的旅游方案? A、B; A、C; B、C 3种有
顺
序无
顺
序一、学情调查、情景导入 观察归纳—形成概念Ⅰ概念讲解二、问题展示、合作探究 探究一:组合定义 一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合. 排列与组合的概念有什么共同点与不同点? 概念讲解二、问题展示、合作探究 排列定义: 一般地,从n个不同元素中取出m (m≤n) 个元素,按照一定的顺序排成一列,叫做从 n 个不同元素中取出 m 个元素的一个排列.组合定义: 一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.共同点: 都要“从n个不同元素中任取m个元素” 不同点: 排列与元素的顺序有关,
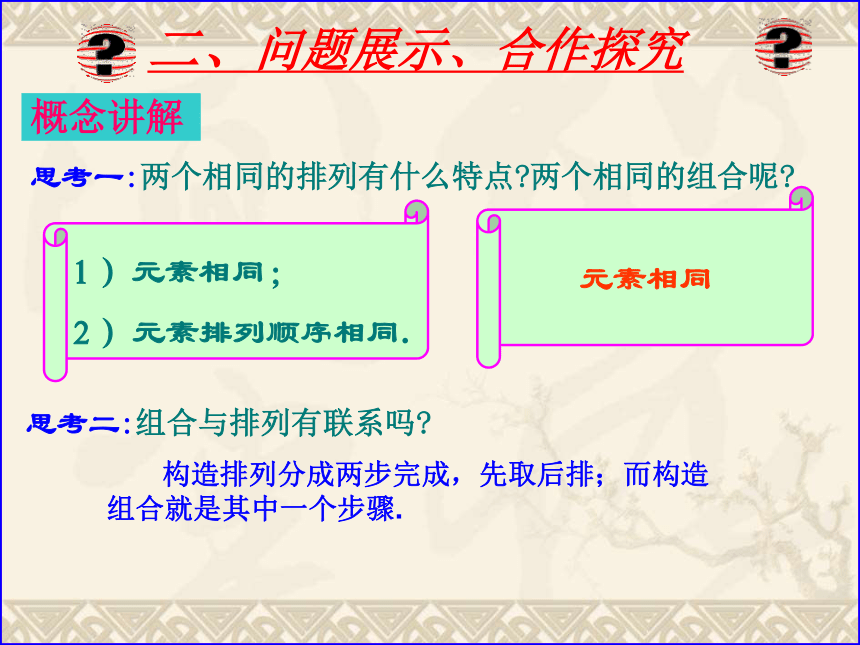
而组合则与元素的顺序无关.概念讲解二、问题展示、合作探究 思考一:两个相同的排列有什么特点?两个相同的组合呢?思考二:组合与排列有联系吗? 构造排列分成两步完成,先取后排;而构造组合就是其中一个步骤.辨析Ⅱ 辨析讨论—深化概念 有无顺序判断下列各事件是排列问题,还是组合问题.
(1)从50个人中选3个人去参加同一种劳动,有多少种不同的选法?
(2)从50个人中选3个人到三个学校参加毕业典礼,有多少种选法?
(3)从1,2,3,…,9九个数字中任取3个,组成一个三位数,这样的三位数共有多少个?
(4)从1,2,3,…,9九个数字中任取3个,然后把这三个数字相加得到一个和,这样的和共有多少个?二、问题展示、合作探究 类比归纳—形成概念 二、问题展示、合作探究 探究二:组合数定义 从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号 表示.注意:
是一个数,应该把它与“组合”区别开来. 如:从3个同学选出2名同学的所有组合个数是:如:从4个景点选出2个进行游览的所有组合个数是:二、问题展示、合作探究 探究三:组合数公式1.写出从a,b,c,d 四个元素中任取三个元素的所有组合。abcabdacdbcd2.从a,b,c,d 四个元素中任取三个元素的排列数与组合数
有什么联系?如何计算3.根据上述分析,求 可分为哪两步?二、问题展示、合作探究 概念讲解 一般地,求从 个不同元素中取出 个元素的排列数,可以分为以下2步: 第1步,先求出从这 个不同元素中取出 个元素的组合数 . 第2步,求每一个组合中 个元素的全排列数 . 根据分步计数原理,得到:因此: 这里 ,且 ,这个公式叫做组合数公式. 二、问题展示、合作探究 例题分析例2.在100件产品中,有98件合格品,2件次品,从这100件产品中任意抽取3件,
(1)有多少种不同的抽法?
(2)抽出的3件中恰好有一件是次品的抽法有多少种?
(3)抽出的3件中至少有1件是次品的抽法有多少种?三、达标检测、巩固提升 梯度一:熟练定义公式
A1. 的值是( ).
A.48 B.49 C.84 D.504
A2.从1,2,3,4,5中取出两个数字组成一个集合,则这样的集合的个数为( ).
A.5 B.10 C.15 D.20
A3.给出下列问题:
①从甲、乙、丙3名同学中选出2名去参加某两个乡镇的社会调查,有多少种选法?
②有4张电影票,要在7人中确定4人去观看,有多少种不同的选法?
③某人射击8枪,击中4枪,且命中的4枪均为2枪连中,则不同的结果有多少种?
其中是组合问题的个数是( ).
A.0 B.1 C.2 D.3三、达标检测、巩固提升 梯度二:巩固定义公式
B1.如果 ,则m等于( ).
A.6 B.7 C.8 D.9
B2.(2014年·大纲卷)有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( ).
A.60种 B.70种 C.75种 D.150种
B3.要从12人中选出5人去参加一项活动.
(1)A,B,C 3人必须入选有多少种不同选法?
(2)A,B,C 3人都不能入选有多少种不同选法?
(3)A,B,C 3人只有1人入选有多少种不同选法?三、达标检测、巩固提升 梯度三:定义公式的灵活应用
C1(2012年·山东卷)现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这卡片不能是同一种颜色,且红色卡片至多1张,不同取法的种数为( )
A.232 B.252 C.472 D.484
C四、知识梳理、归纳总结 排列 有无顺序 组合 排列是
选择后
再排序
的结果
组合是
选择的
结 果组合数公式转化
顺
序无
顺
序一、学情调查、情景导入 观察归纳—形成概念Ⅰ概念讲解二、问题展示、合作探究 探究一:组合定义 一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合. 排列与组合的概念有什么共同点与不同点? 概念讲解二、问题展示、合作探究 排列定义: 一般地,从n个不同元素中取出m (m≤n) 个元素,按照一定的顺序排成一列,叫做从 n 个不同元素中取出 m 个元素的一个排列.组合定义: 一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.共同点: 都要“从n个不同元素中任取m个元素” 不同点: 排列与元素的顺序有关,
而组合则与元素的顺序无关.概念讲解二、问题展示、合作探究 思考一:两个相同的排列有什么特点?两个相同的组合呢?思考二:组合与排列有联系吗? 构造排列分成两步完成,先取后排;而构造组合就是其中一个步骤.辨析Ⅱ 辨析讨论—深化概念 有无顺序判断下列各事件是排列问题,还是组合问题.
(1)从50个人中选3个人去参加同一种劳动,有多少种不同的选法?
(2)从50个人中选3个人到三个学校参加毕业典礼,有多少种选法?
(3)从1,2,3,…,9九个数字中任取3个,组成一个三位数,这样的三位数共有多少个?
(4)从1,2,3,…,9九个数字中任取3个,然后把这三个数字相加得到一个和,这样的和共有多少个?二、问题展示、合作探究 类比归纳—形成概念 二、问题展示、合作探究 探究二:组合数定义 从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号 表示.注意:
是一个数,应该把它与“组合”区别开来. 如:从3个同学选出2名同学的所有组合个数是:如:从4个景点选出2个进行游览的所有组合个数是:二、问题展示、合作探究 探究三:组合数公式1.写出从a,b,c,d 四个元素中任取三个元素的所有组合。abcabdacdbcd2.从a,b,c,d 四个元素中任取三个元素的排列数与组合数
有什么联系?如何计算3.根据上述分析,求 可分为哪两步?二、问题展示、合作探究 概念讲解 一般地,求从 个不同元素中取出 个元素的排列数,可以分为以下2步: 第1步,先求出从这 个不同元素中取出 个元素的组合数 . 第2步,求每一个组合中 个元素的全排列数 . 根据分步计数原理,得到:因此: 这里 ,且 ,这个公式叫做组合数公式. 二、问题展示、合作探究 例题分析例2.在100件产品中,有98件合格品,2件次品,从这100件产品中任意抽取3件,
(1)有多少种不同的抽法?
(2)抽出的3件中恰好有一件是次品的抽法有多少种?
(3)抽出的3件中至少有1件是次品的抽法有多少种?三、达标检测、巩固提升 梯度一:熟练定义公式
A1. 的值是( ).
A.48 B.49 C.84 D.504
A2.从1,2,3,4,5中取出两个数字组成一个集合,则这样的集合的个数为( ).
A.5 B.10 C.15 D.20
A3.给出下列问题:
①从甲、乙、丙3名同学中选出2名去参加某两个乡镇的社会调查,有多少种选法?
②有4张电影票,要在7人中确定4人去观看,有多少种不同的选法?
③某人射击8枪,击中4枪,且命中的4枪均为2枪连中,则不同的结果有多少种?
其中是组合问题的个数是( ).
A.0 B.1 C.2 D.3三、达标检测、巩固提升 梯度二:巩固定义公式
B1.如果 ,则m等于( ).
A.6 B.7 C.8 D.9
B2.(2014年·大纲卷)有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( ).
A.60种 B.70种 C.75种 D.150种
B3.要从12人中选出5人去参加一项活动.
(1)A,B,C 3人必须入选有多少种不同选法?
(2)A,B,C 3人都不能入选有多少种不同选法?
(3)A,B,C 3人只有1人入选有多少种不同选法?三、达标检测、巩固提升 梯度三:定义公式的灵活应用
C1(2012年·山东卷)现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这卡片不能是同一种颜色,且红色卡片至多1张,不同取法的种数为( )
A.232 B.252 C.472 D.484
C四、知识梳理、归纳总结 排列 有无顺序 组合 排列是
选择后
再排序
的结果
组合是
选择的
结 果组合数公式转化
