2.1 函数(通用)课件(27张PPT)
文档属性
| 名称 | 2.1 函数(通用)课件(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 109.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 00:00:00 | ||
图片预览





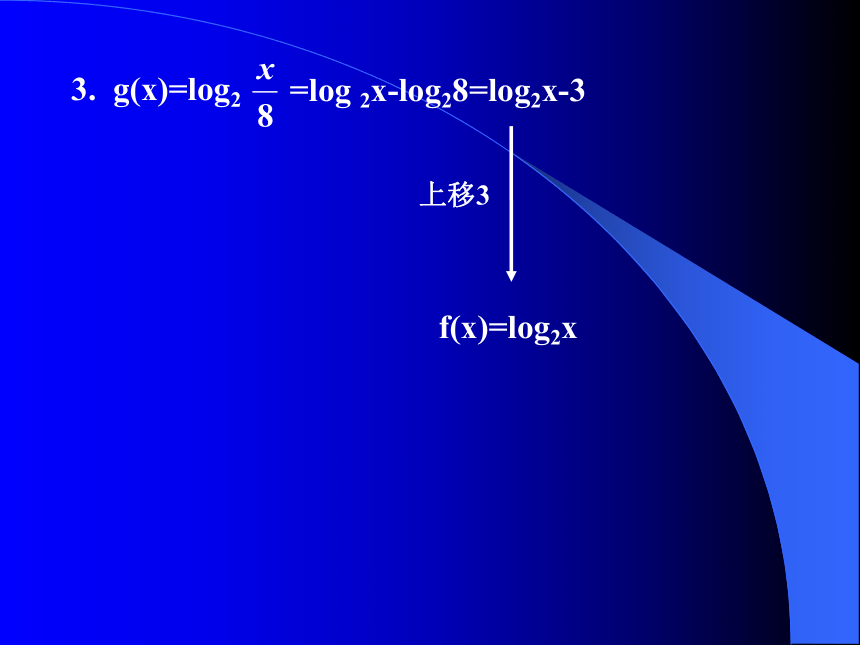
文档简介
课件27张PPT。函数的图象变换
2014年,共18套高考卷,9套考图像变换,1套考识图题
2015年,共15套高考卷,6套考图像变换,2套考识图题
2016年,共9套高考卷,6套考图像变换,1套考识图题
2017年,共8套高考卷,2套考图像变换,1套考识图题
2018年,全国2卷3题,考识图题图像变换是高考的高频考点:
考察题型:
1.结合三角函数考察平移和伸缩
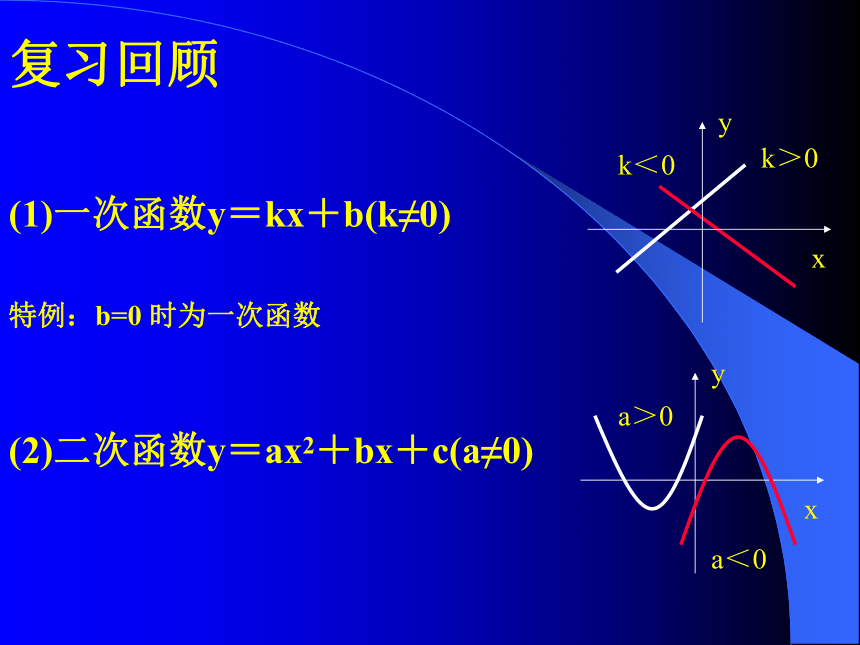
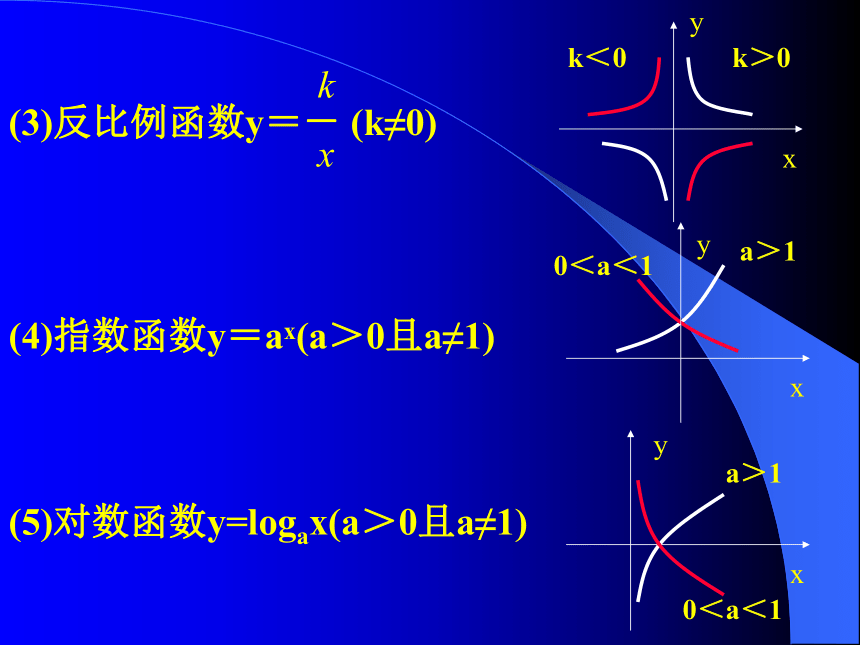
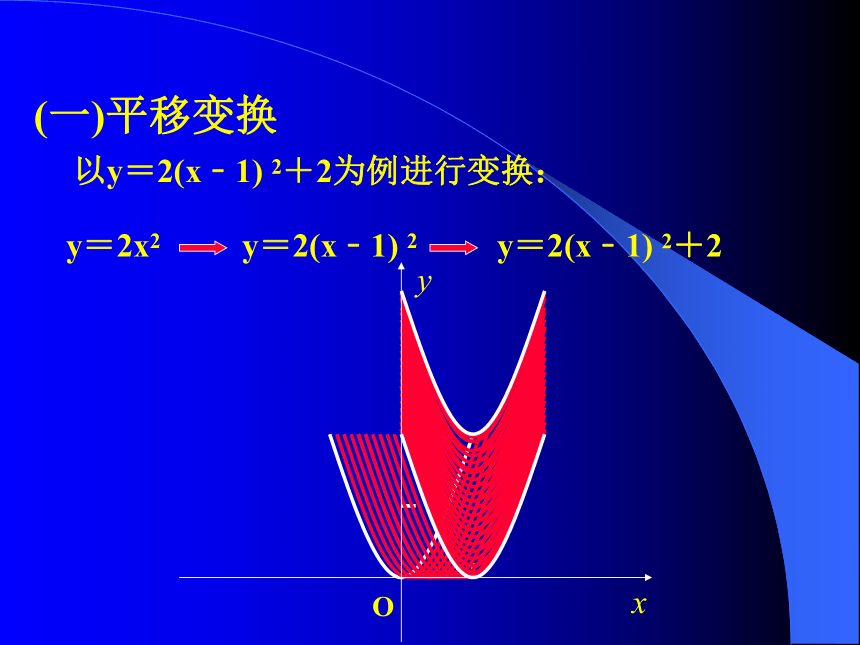
2.结合函数与方程考察平移和翻折复习回顾 (1)一次函数y=kx+b(k≠0) k>0k<0特例:b=0 时为一次函数 (2)二次函数y=ax2+bx+c(a≠0) a>0a<0k>0k<0(4)指数函数y=ax(a>0且a≠1) a>10<a<1(5)对数函数y=logax(a>0且a≠1) a>10<a<1以y=2(x﹣1) 2+2为例进行变换:y=2(x﹣1) 2y=2x2(一)平移变换y=2(x﹣1) 2+2 y=f(x) 平移变换 (左加右减)(上加下减)左移h个单位右移h个单位下移k个单位上移k个单位(1)左右平移:设h>0(2)上下平移: 设k>0y=f(x-h)
y=f(x+h) y=f(x) y=f(x) -ky=f(x) y=f(x) y=f(x) +k2. y=sin2x左y=sin[2(x+ )]=sin(2x+ )=cos2x 上1y=cos2x+1只针对x
与2无关f(x)=log2x3. g(x)=log2 上移3=log 2x-log28=log2x-3 解:左2 上3体验高考:(2016年全国2.7题)若将函数y=2sin2x的图像向左平
移 个单位长度,则平移后图像的对称轴为( )
A. B.
C. D.By=2sin2x左移析:=2sin(2x+ )由2x+ =k + 解得:22-1ACBOy=log2xy=log2(x+1)体验高考:C(1,1)(1)y=f(x)与y=f(﹣ x)的图象关于 对称y轴(x,y)(-x,y)(二)对称变换 y=f(x)y=f(﹣ x) (2)y=f(x)与y= ﹣ f (x)的图象关于 对称x轴 (x,y)(x,-y)y=f(x)y= ﹣ f (x)(3)y=f(x)与y=﹣f(﹣x)的图象关于 对称原点(x,y)(-x,-y)y=f(x)y=﹣f(﹣x)(4)y=f(x-a)与y=f (a-x)的图象关于 对称=f[-(x-a)]y=f(x)y=f(-x)右移a右移ax=ay=f(x)y=f(﹣ x)y=f[-(x-a)]y=f(x-a)x(5)y=f(x-a)与y=-f (a-x)的图象关于 对称(a,0)= -f[-(x-a)]yy=f(x)y= -f(-x)右移a右移ay=f(x)y=﹣f(﹣x)y=f(x-a)y=-f (a-x)(6)y=f(x)与y=f -1(x)的图象关于 对称直线y=x9. y=f(x)与y=ex关于y轴对称右移1y=e-x 左移1f(x)=e-(x+1)y=exy=e-x 体验高考:(2014年大纲卷.12题)函数y=f(x)的图像与函数y=g(x)的图像关于直线x+y=0对称,则y=f(x)的反函数是( )A.y=g(x) B.y=g(-x)
C.y= -g(x) D.y=-g(-x)Dxyy=f(x)y=g(x)y=f-1(x)(三)翻折变换 1、上翻:函数y=|f(x)|的图象,保留y=f(x)在x轴上方部分,再将其在x轴下方部分沿x轴对称地翻折到上方,即得.f(x) 2、左翻:函数y=f(|x|)的图像,去掉y=f(x)在y轴左侧部分,再将其在y轴右侧部分到y轴左侧,并保留右侧部分即得。(偶函数)沿y轴对称地翻折f(x)(x>0)f(|x|)练习: 作函数下列的图象:(1)y=|2x-1| (2) y=log2|x|-111-1y= 2x-1y=log2 x15. 直线y=1与曲线y=x2-|x|+a有四个交点y= 1-ay=x2- x y=x2-|x|与y=1-a的图像有四个交点1-1y= x2-116. 方程|x2-1|=a有3个根-111y=ay=|x2-1|与y=a的图像有三个交点a=1(2014年山东.8题)已知函数f(x)=|x-2|+1,g(x)=kx.若方程f(x)=g(x)有两个不相等的实根,则实数k的取值范围( )
A. (0, ) B.( ,1)
C. (1, 2) D.(2, )体验高考:By=x-2y=|x-2|f(x)=|x-2|+1谢谢!
2014年,共18套高考卷,9套考图像变换,1套考识图题
2015年,共15套高考卷,6套考图像变换,2套考识图题
2016年,共9套高考卷,6套考图像变换,1套考识图题
2017年,共8套高考卷,2套考图像变换,1套考识图题
2018年,全国2卷3题,考识图题图像变换是高考的高频考点:
考察题型:
1.结合三角函数考察平移和伸缩
2.结合函数与方程考察平移和翻折复习回顾 (1)一次函数y=kx+b(k≠0) k>0k<0特例:b=0 时为一次函数 (2)二次函数y=ax2+bx+c(a≠0) a>0a<0k>0k<0(4)指数函数y=ax(a>0且a≠1) a>10<a<1(5)对数函数y=logax(a>0且a≠1) a>10<a<1以y=2(x﹣1) 2+2为例进行变换:y=2(x﹣1) 2y=2x2(一)平移变换y=2(x﹣1) 2+2 y=f(x) 平移变换 (左加右减)(上加下减)左移h个单位右移h个单位下移k个单位上移k个单位(1)左右平移:设h>0(2)上下平移: 设k>0y=f(x-h)
y=f(x+h) y=f(x) y=f(x) -ky=f(x) y=f(x) y=f(x) +k2. y=sin2x左y=sin[2(x+ )]=sin(2x+ )=cos2x 上1y=cos2x+1只针对x
与2无关f(x)=log2x3. g(x)=log2 上移3=log 2x-log28=log2x-3 解:左2 上3体验高考:(2016年全国2.7题)若将函数y=2sin2x的图像向左平
移 个单位长度,则平移后图像的对称轴为( )
A. B.
C. D.By=2sin2x左移析:=2sin(2x+ )由2x+ =k + 解得:22-1ACBOy=log2xy=log2(x+1)体验高考:C(1,1)(1)y=f(x)与y=f(﹣ x)的图象关于 对称y轴(x,y)(-x,y)(二)对称变换 y=f(x)y=f(﹣ x) (2)y=f(x)与y= ﹣ f (x)的图象关于 对称x轴 (x,y)(x,-y)y=f(x)y= ﹣ f (x)(3)y=f(x)与y=﹣f(﹣x)的图象关于 对称原点(x,y)(-x,-y)y=f(x)y=﹣f(﹣x)(4)y=f(x-a)与y=f (a-x)的图象关于 对称=f[-(x-a)]y=f(x)y=f(-x)右移a右移ax=ay=f(x)y=f(﹣ x)y=f[-(x-a)]y=f(x-a)x(5)y=f(x-a)与y=-f (a-x)的图象关于 对称(a,0)= -f[-(x-a)]yy=f(x)y= -f(-x)右移a右移ay=f(x)y=﹣f(﹣x)y=f(x-a)y=-f (a-x)(6)y=f(x)与y=f -1(x)的图象关于 对称直线y=x9. y=f(x)与y=ex关于y轴对称右移1y=e-x 左移1f(x)=e-(x+1)y=exy=e-x 体验高考:(2014年大纲卷.12题)函数y=f(x)的图像与函数y=g(x)的图像关于直线x+y=0对称,则y=f(x)的反函数是( )A.y=g(x) B.y=g(-x)
C.y= -g(x) D.y=-g(-x)Dxyy=f(x)y=g(x)y=f-1(x)(三)翻折变换 1、上翻:函数y=|f(x)|的图象,保留y=f(x)在x轴上方部分,再将其在x轴下方部分沿x轴对称地翻折到上方,即得.f(x) 2、左翻:函数y=f(|x|)的图像,去掉y=f(x)在y轴左侧部分,再将其在y轴右侧部分到y轴左侧,并保留右侧部分即得。(偶函数)沿y轴对称地翻折f(x)(x>0)f(|x|)练习: 作函数下列的图象:(1)y=|2x-1| (2) y=log2|x|-111-1y= 2x-1y=log2 x15. 直线y=1与曲线y=x2-|x|+a有四个交点y= 1-ay=x2- x y=x2-|x|与y=1-a的图像有四个交点1-1y= x2-116. 方程|x2-1|=a有3个根-111y=ay=|x2-1|与y=a的图像有三个交点a=1(2014年山东.8题)已知函数f(x)=|x-2|+1,g(x)=kx.若方程f(x)=g(x)有两个不相等的实根,则实数k的取值范围( )
A. (0, ) B.( ,1)
C. (1, 2) D.(2, )体验高考:By=x-2y=|x-2|f(x)=|x-2|+1谢谢!
