2.1.2 函数的表示方法 课件(22张PPT)
文档属性
| 名称 | 2.1.2 函数的表示方法 课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 21:38:55 | ||
图片预览







文档简介
课件22张PPT。数学学科 高一年级 人教版必修1 2.1.2 函数的表示方法
(1)表示两个变量之间函数关系的方法有几种?
分别是什么?
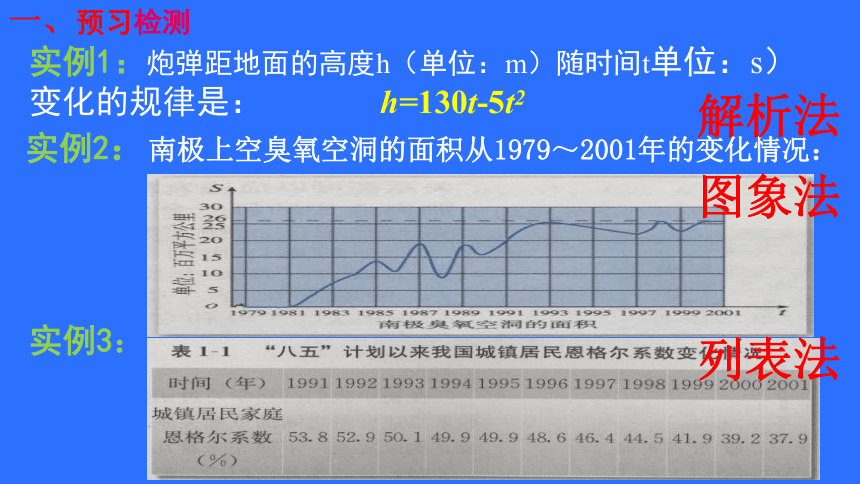
(2)函数的各种表示法分别有什么特点?预习课本p38~42,思考并完成以下问题一、预习检测实例1:炮弹距地面的高度h(单位:m)随时间t单位:s)变化的规律是: h=130t-5t2实例2:南极上空臭氧空洞的面积从1979~2001年的变化情况:实例3:解析法图象法列表法函数的表示法
(1)列表法
通过列出 与 的表来表示函数关系的方法叫做列表法.
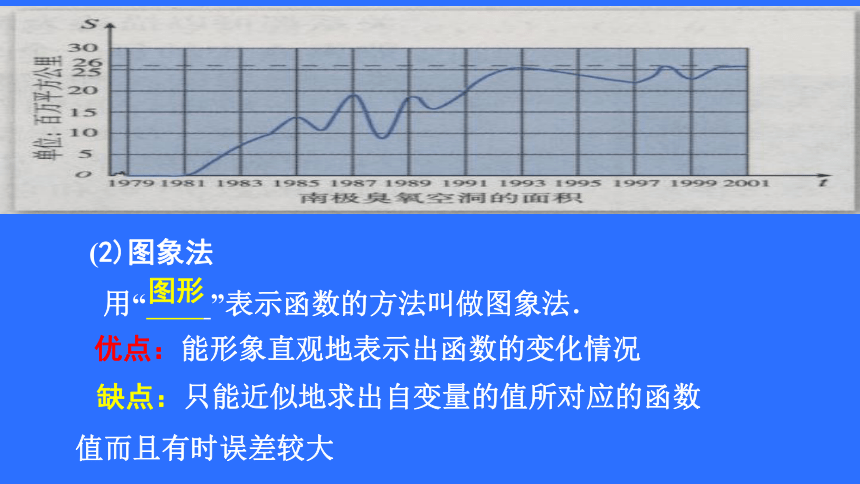
自变量对应函数值优点:不需要计算就可以直接看出与自变量相对应的函数值.缺点:它只能表示自变量可以一一列出的函数关系.二、新知自解(2)图象法
用“ ”表示函数的方法叫做图象法.图形 优点:能形象直观地表示出函数的变化情况 缺点:只能近似地求出自变量的值所对应的函数 值而且有时误差较大优点:一是简明、全面地概括了变量间的关系;二是利用解析式 可以求出任意一个函数值.缺点:不够形象、直观、具体,而且并不是所有的函数都能用解析法表示出来.函数的表示法
(3)解析法(公式法)
如果在函数y=f(x)(x∈A)中,f(x)是用_______________ 来表达的,则这种表示函数的方法叫做解析法.代数式(或解析式)例1、某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元;试用函数的三种表示法表示函数 y=f (x) .分析: “y=f (x)”可以用哪三种方法表示?. 三、例题分析它可以是解析法,可以是图象法,也可以是列表法.例3、某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元;试用函数的三种表示法表示函数 y=f (x) .解:(1)用解析法可将函数 y=f (x)表示为:
(2)用列表法可将函数 y=f (x)表示为:
(3)用图象法如右图:, x∈{1 , 2 , 3 , 4 , 5 }笔记本数 x钱数 y1 2 3 4 5 5 10 15 20 25 三、例题分析y=5x思考1:
若例1中的函数y=f(x)的定义域改为 [1,5],则其将图象会发生怎样的变化?
一条线段五个点:(1,5),(2,10),(3,15),(4,20),(5,25)(1) 出生率与年份间的函数关系:能不能用解析法 ?能不能用图象法?并非所有的函数都能用这三种方法来表示! 思考2:所有函数都能用这三种方法表示吗? 例2、下表是某校高一(1)班三位同学在高一学年度几次数学测试的成绩及班级平均分表: 请你对这三个同学在高一学年度的数学学习情况做一个分析.解析:从表中可知每位同学在每次测试中的成绩,但不易分析每位同学的成绩变化情况。
若将“成绩”与“测试序号”之间的关系用函数图象表示出来,那么将…… 二、例题分析 若将“成绩”与“测试序号”之间的关系用函数图象表示出来,直观反映成绩变
化: 分析上图:
王伟同学的数学成绩始终高于班平均水平, 学习情况较为稳定且成绩优秀
张城同学数学成绩不稳定, 总在班平均水平上下波动,且波动幅度较大
赵磊同学数学成绩低于班级平均水平, 但他的成绩呈上升趋势,表明他的 成
绩在稳步提高.虚线部分并不是图象的一部分思考3:
如何判断图形是否为函数图象呢?随练:下列四个图象中,不是函数图象的是( )B←任意性、唯一性ABCD例题探究例3:作函数 的图像解:在这个函数的定义域内,从0开始适当的取若干个x的值算出对应的函数值,列出函数的对应值表.将表格中的点标在坐标系中,即可得出函数的图像. 描点法作函数图象的三个关注点
(1)画函数图象时首先关注函数的定义域,即在定义域内作图.
(2)函数图象可能是平滑的曲线,也可能是一群孤立的点,定义域以外的部分有时可用虚线来衬托整个图象.
(3)画图时要注意关键点,如图象的顶点、区间端点、与坐标轴的交点等,要分清这些关键点是实心点还是空心点.反思与感悟
作出下列函数的图象并求出其值域.
(1) y=2x+1,x∈[0,2];(2)y=x2+2x,x∈[-2,2].
解: (1)列表:当x∈[0,2]时,图象是直线的一部分,
观察图象可知,其值域为[1,5].(2) y=x2+2x,x∈[-2,2].解: 列表:画图象,图象是抛物线y=x2+2x在-2≤x≤2之间的部分.
由图可得函数的值域是[-1,8]. 例4. (教材P41) 已知函数y=f(n), f(0)=1,f(n)=nf(n-1),
n是正整数,求f(1) ,f(2),f(3) ,f(4), f(5) .解:因为f(0)=1,所以例题探究
(教材P41.练习A.3)
已知函数y=f(n),满足f(1)=8,且f(n+1)=f(n)+7, n是正整数,求f(2),f(3),f(4).
(1)函数的三种表示方法的优缺点方法*规律*小结方法*规律*小结 (2) 列表法、图像法、解析法是从三个不同角度刻画自变量与函数值的
对应关系,同一个函数可以用不同的方法表示出来. 2. 某问答游戏的规则是:共5道选择题,基础分为50分,每答错1道题扣10分,答对不扣分.试分别用列表法、图象法、解析法表示一个参与者的得分y与答错题目道数x(x∈{0,1,2,3,4,5})之间的函数关系. 课堂检测 1. (教材P42.练习B.3)
已知函数y=f(n),满足f(1)=2,且f(n+1)=3f(n),n是正整数,求f(2),f(3),f(4), f(5).
(1)表示两个变量之间函数关系的方法有几种?
分别是什么?
(2)函数的各种表示法分别有什么特点?预习课本p38~42,思考并完成以下问题一、预习检测实例1:炮弹距地面的高度h(单位:m)随时间t单位:s)变化的规律是: h=130t-5t2实例2:南极上空臭氧空洞的面积从1979~2001年的变化情况:实例3:解析法图象法列表法函数的表示法
(1)列表法
通过列出 与 的表来表示函数关系的方法叫做列表法.
自变量对应函数值优点:不需要计算就可以直接看出与自变量相对应的函数值.缺点:它只能表示自变量可以一一列出的函数关系.二、新知自解(2)图象法
用“ ”表示函数的方法叫做图象法.图形 优点:能形象直观地表示出函数的变化情况 缺点:只能近似地求出自变量的值所对应的函数 值而且有时误差较大优点:一是简明、全面地概括了变量间的关系;二是利用解析式 可以求出任意一个函数值.缺点:不够形象、直观、具体,而且并不是所有的函数都能用解析法表示出来.函数的表示法
(3)解析法(公式法)
如果在函数y=f(x)(x∈A)中,f(x)是用_______________ 来表达的,则这种表示函数的方法叫做解析法.代数式(或解析式)例1、某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元;试用函数的三种表示法表示函数 y=f (x) .分析: “y=f (x)”可以用哪三种方法表示?. 三、例题分析它可以是解析法,可以是图象法,也可以是列表法.例3、某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元;试用函数的三种表示法表示函数 y=f (x) .解:(1)用解析法可将函数 y=f (x)表示为:
(2)用列表法可将函数 y=f (x)表示为:
(3)用图象法如右图:, x∈{1 , 2 , 3 , 4 , 5 }笔记本数 x钱数 y1 2 3 4 5 5 10 15 20 25 三、例题分析y=5x思考1:
若例1中的函数y=f(x)的定义域改为 [1,5],则其将图象会发生怎样的变化?
一条线段五个点:(1,5),(2,10),(3,15),(4,20),(5,25)(1) 出生率与年份间的函数关系:能不能用解析法 ?能不能用图象法?并非所有的函数都能用这三种方法来表示! 思考2:所有函数都能用这三种方法表示吗? 例2、下表是某校高一(1)班三位同学在高一学年度几次数学测试的成绩及班级平均分表: 请你对这三个同学在高一学年度的数学学习情况做一个分析.解析:从表中可知每位同学在每次测试中的成绩,但不易分析每位同学的成绩变化情况。
若将“成绩”与“测试序号”之间的关系用函数图象表示出来,那么将…… 二、例题分析 若将“成绩”与“测试序号”之间的关系用函数图象表示出来,直观反映成绩变
化: 分析上图:
王伟同学的数学成绩始终高于班平均水平, 学习情况较为稳定且成绩优秀
张城同学数学成绩不稳定, 总在班平均水平上下波动,且波动幅度较大
赵磊同学数学成绩低于班级平均水平, 但他的成绩呈上升趋势,表明他的 成
绩在稳步提高.虚线部分并不是图象的一部分思考3:
如何判断图形是否为函数图象呢?随练:下列四个图象中,不是函数图象的是( )B←任意性、唯一性ABCD例题探究例3:作函数 的图像解:在这个函数的定义域内,从0开始适当的取若干个x的值算出对应的函数值,列出函数的对应值表.将表格中的点标在坐标系中,即可得出函数的图像. 描点法作函数图象的三个关注点
(1)画函数图象时首先关注函数的定义域,即在定义域内作图.
(2)函数图象可能是平滑的曲线,也可能是一群孤立的点,定义域以外的部分有时可用虚线来衬托整个图象.
(3)画图时要注意关键点,如图象的顶点、区间端点、与坐标轴的交点等,要分清这些关键点是实心点还是空心点.反思与感悟
作出下列函数的图象并求出其值域.
(1) y=2x+1,x∈[0,2];(2)y=x2+2x,x∈[-2,2].
解: (1)列表:当x∈[0,2]时,图象是直线的一部分,
观察图象可知,其值域为[1,5].(2) y=x2+2x,x∈[-2,2].解: 列表:画图象,图象是抛物线y=x2+2x在-2≤x≤2之间的部分.
由图可得函数的值域是[-1,8]. 例4. (教材P41) 已知函数y=f(n), f(0)=1,f(n)=nf(n-1),
n是正整数,求f(1) ,f(2),f(3) ,f(4), f(5) .解:因为f(0)=1,所以例题探究
(教材P41.练习A.3)
已知函数y=f(n),满足f(1)=8,且f(n+1)=f(n)+7, n是正整数,求f(2),f(3),f(4).
(1)函数的三种表示方法的优缺点方法*规律*小结方法*规律*小结 (2) 列表法、图像法、解析法是从三个不同角度刻画自变量与函数值的
对应关系,同一个函数可以用不同的方法表示出来. 2. 某问答游戏的规则是:共5道选择题,基础分为50分,每答错1道题扣10分,答对不扣分.试分别用列表法、图象法、解析法表示一个参与者的得分y与答错题目道数x(x∈{0,1,2,3,4,5})之间的函数关系. 课堂检测 1. (教材P42.练习B.3)
已知函数y=f(n),满足f(1)=2,且f(n+1)=3f(n),n是正整数,求f(2),f(3),f(4), f(5).
