2.2.1 一次函数的性质与图象 课件(19张PPT)
文档属性
| 名称 | 2.2.1 一次函数的性质与图象 课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 822.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 00:00:00 | ||
图片预览






文档简介
课件19张PPT。2.2.1一次函数的性质与图像1.理解掌握一次函数的概念、图象和性质,提高学生分析问题的能力,培养分类讨论及数形结合思想.
2.渗透由特殊到一般由具体到抽象的数学思想方法。
3.让学生了解数学源于实际,应用于实际,培养学生的应用意识。
一次函数的性质与图象.
一次函数的性质的应用.Learning Together目标重点难点1.观察下列函数有什么共同特点:
①y=2x-1; ②y=3x+6;
③y=-x; ④y=复习导入温故知新1.一次函数的定义?.练习:指出下列函数中的一次函数——
(1)y=-x; (2)y= ;
(3)y=9x-2; (4)y=x2+1.2.一次函数的图象是什么形状?思考:
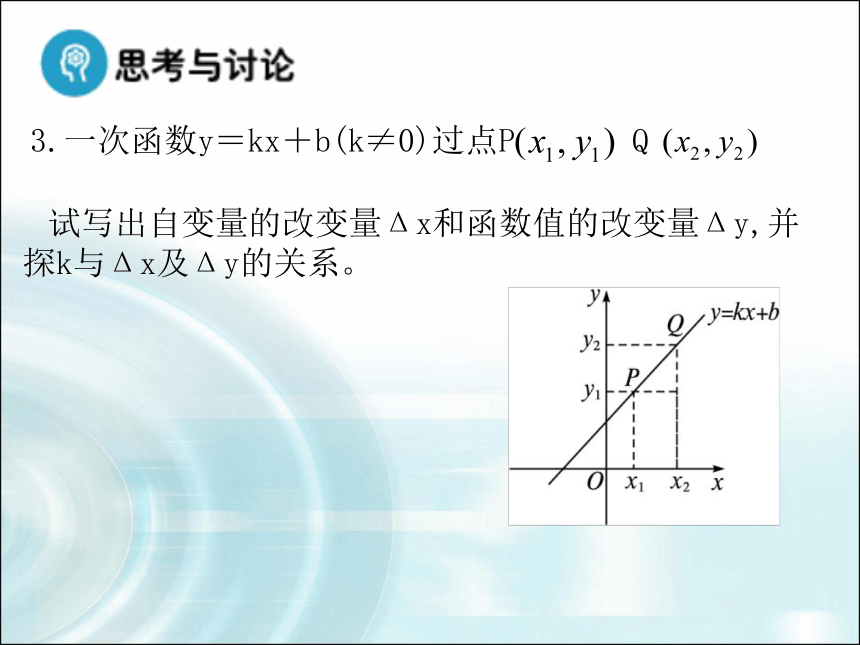
一次函数的图像是直线,直线对应的函数都是 一次函数么?试写出自变量的改变量Δx和函数值的改变量Δy,并探k与Δx及Δy的关系。1. 下列函数中,y随x的增大而增大的是( )D. y= –2x-7A. y=–3xC2. 一次函数y=(a+1)x+5中,y的值随x的值增大而
减小,则a满足________ .a< –1B. y= –0.5x+14.探讨一次函数的奇偶性
当b=0时,一次函数变为正比例函数,是奇函数;
当b≠0时,它既不是奇函数,也不是偶函数.5.写出一次函数y=kx+b与两坐标轴的交点的坐标.
与x轴的交点为
与y轴的交点为(0,b).思考:我们如何快速准确的画出一次函数的图像?根据函数图象确定k,b的取值范围
yxoK>o, b=oyxoK>0, bo, b>0yxoK<0, b=0yx0K<0, b<0yxoK<0, b>06.归纳一次函数y=kx+b的性质
(3)单调性:当k>0时,一次函数y=kx+b在R上是增函数;
当k<0时,一次函数y=kx+b在R上是减函数.
(4)奇偶性:当b=0时,一次函数变为正比例函数,
是奇函数;当b≠0时,它既不是奇函数,也不是偶函数.
(5)图象:形状是直线,与x轴的交点为 ,
与y轴的交点为(0,b).(1)定义域:R.
(2)值域:R.
【例1】 已知函数y=(2m-1)x+1-3m,当m为何值时,
(1)这个函数为正比例函数;
(2)这个函数为一次函数;
(3)函数值y随x的增大而减小;
【变式】 已知一次函数y=(m-2)x+m2-3m-2,它的图象在y轴上的截距为-4,则m的值为( )
A.-4 B.2 C.1 D.2或1【例2】求函数y=-5x-1,x∈[1,4]的最小值.变式训:1: 已知函数y=2x+b在区间[-1,3]上的最大值是7,求实数b的值.
变式训练2:已知函数y=(b-1)x+ 在区间[-1,3]上的最大值是7,求实数b的值.【例3】 小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行.如图所示,图中的两条线段分别表示小东、小明离B地的距离y(单位:km)与所用时间x(单位:h)的关系.
(1)试用文字说明交点P所表示的实际意义;
(2)试求出A,B两地之间的距离.解:(1)交点P所表示的实际意义:经过2.5 h后,小东与小明在距离B地7.5 km处相遇.
(2)设小东离B地的距离y1与所用时间x之间的关系式为y1=kx+b(k≠0),又y1经过点P(2.5,7.5),点(4,0),
即y1=-5x+20.当x=0时,y1=20.
故A,B两地之间的距离为20 km.y=4x+1y=x+2y=-2x+4本节课,你有哪些收获?作业A组2、3、5
B组1谢谢!
2.渗透由特殊到一般由具体到抽象的数学思想方法。
3.让学生了解数学源于实际,应用于实际,培养学生的应用意识。
一次函数的性质与图象.
一次函数的性质的应用.Learning Together目标重点难点1.观察下列函数有什么共同特点:
①y=2x-1; ②y=3x+6;
③y=-x; ④y=复习导入温故知新1.一次函数的定义?.练习:指出下列函数中的一次函数——
(1)y=-x; (2)y= ;
(3)y=9x-2; (4)y=x2+1.2.一次函数的图象是什么形状?思考:
一次函数的图像是直线,直线对应的函数都是 一次函数么?试写出自变量的改变量Δx和函数值的改变量Δy,并探k与Δx及Δy的关系。1. 下列函数中,y随x的增大而增大的是( )D. y= –2x-7A. y=–3xC2. 一次函数y=(a+1)x+5中,y的值随x的值增大而
减小,则a满足________ .a< –1B. y= –0.5x+14.探讨一次函数的奇偶性
当b=0时,一次函数变为正比例函数,是奇函数;
当b≠0时,它既不是奇函数,也不是偶函数.5.写出一次函数y=kx+b与两坐标轴的交点的坐标.
与x轴的交点为
与y轴的交点为(0,b).思考:我们如何快速准确的画出一次函数的图像?根据函数图象确定k,b的取值范围
yxoK>o, b=oyxoK>0, b
(3)单调性:当k>0时,一次函数y=kx+b在R上是增函数;
当k<0时,一次函数y=kx+b在R上是减函数.
(4)奇偶性:当b=0时,一次函数变为正比例函数,
是奇函数;当b≠0时,它既不是奇函数,也不是偶函数.
(5)图象:形状是直线,与x轴的交点为 ,
与y轴的交点为(0,b).(1)定义域:R.
(2)值域:R.
【例1】 已知函数y=(2m-1)x+1-3m,当m为何值时,
(1)这个函数为正比例函数;
(2)这个函数为一次函数;
(3)函数值y随x的增大而减小;
【变式】 已知一次函数y=(m-2)x+m2-3m-2,它的图象在y轴上的截距为-4,则m的值为( )
A.-4 B.2 C.1 D.2或1【例2】求函数y=-5x-1,x∈[1,4]的最小值.变式训:1: 已知函数y=2x+b在区间[-1,3]上的最大值是7,求实数b的值.
变式训练2:已知函数y=(b-1)x+ 在区间[-1,3]上的最大值是7,求实数b的值.【例3】 小东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行.如图所示,图中的两条线段分别表示小东、小明离B地的距离y(单位:km)与所用时间x(单位:h)的关系.
(1)试用文字说明交点P所表示的实际意义;
(2)试求出A,B两地之间的距离.解:(1)交点P所表示的实际意义:经过2.5 h后,小东与小明在距离B地7.5 km处相遇.
(2)设小东离B地的距离y1与所用时间x之间的关系式为y1=kx+b(k≠0),又y1经过点P(2.5,7.5),点(4,0),
即y1=-5x+20.当x=0时,y1=20.
故A,B两地之间的距离为20 km.y=4x+1y=x+2y=-2x+4本节课,你有哪些收获?作业A组2、3、5
B组1谢谢!
