3.1.2 指数函数 课件(21张PPT)
文档属性
| 名称 | 3.1.2 指数函数 课件(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 243.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 21:38:32 | ||
图片预览








文档简介
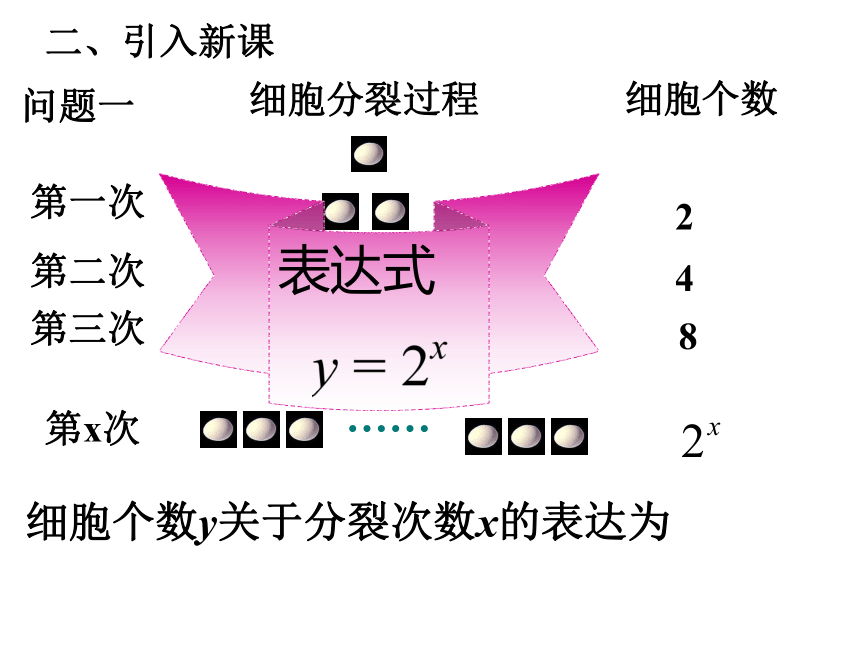
课件21张PPT。 3.1.2指数函数 一、复习旧知: 1.正分数指数幂的定义:2.负分数指数幂的定义:3.0的正分数指数幂等于 0 ,0的负分数指数幂没有意义二、引入新课细胞分裂过程细胞个数第一次第二次第三次2 84………… 第x次……细胞个数y关于分裂次数x的表达为问题一问题二 一种放射性物质不断衰变为其他物质,每经过一年,剩留的质量约是原来的84%,求出这种物质的剩留量y随时间x(单位:年)变化的函数关系。 我们从上面两个问题中抽象得到两个函数关系式: 这两个函数有何共同特征? 一、指数函数1.定义:一般地,我们把形如的函数叫做指数函数,其中是自变量,函数的定义域是注意 (1) 为一个整体,前面系数为1
(2)自变量 在指数的位置上且为单个
(3)说明:为什么规定底数a大于0且不等于1?(1)(3)若a=1时,函数值y=1,没有研究的必要.练一练:下列函数是指数函数吗,为什么?在同一坐标系中分别作出如下函数的图像: 列表如下:2.指数函数的图象:观察右边图象,回答下列问题:问题一:
图象分别在哪几个象限?问题二:图象中有哪些特殊的点?
答:四个图象都经过点____.
问题三:图象的上升、下降与底数a有联系吗?
答:当底数__时图象上升;当底数____时图象下降.
答:四个图象都在第____象限Ⅰ、Ⅱ2.指数函数的图象3.根据指数函数的图象研究它的性质R(0,+∞)(0,1)增函数减函数当 x > 0 时,y > 1.
当 x < 0 时,. 0< y < 1
当 x < 0 时,y > 1;
当 x > 0 时, 0< y < 1。例2、比较下列各题中两个值的大小:(1)1.72.5与1.73(2)0.8-0.1与0.8-0.2 归纳: 两个同底的指数幂比较大小,可构造以该底数为底的指数函数再根据函数的单调性,比较指数的大小解(1)底数都是1.7 , ∴ 又∵2 .5<3,∵ 在R上是增函数 (2)可考查指数函数∴ 在R上是减函数∵ 0.8 <1又∵ ,故考查指数函数 ∴ < ∴ (4) (4)由指数函数的性质知: 1.70.3>1.7 0 =1 归纳:不同底的幂的大小比较,常可借用中间量1或0来比较。(3) 1.70.3与1解:(3)因为1=1.70,而由指数函数的性质知:函数 为增函数,而0.3>0,
故1.70.3 >1.70即1.70.3 > 1.0.93.1<0.90=1, 故: 1.70.3>0.93.1. 例3、(1)若 , 则m与n的大小如何?
解:(1)构造指数函数∵ 所以此函数为减函数又∵∴(2)构造函数∵∴此函数为增函数又∵∴即三、小结 想一想:这节课你收获到了什么?必做 P92, 练习A中1,2
选做 练习B中1,2,3四、作业本节课结束
(2)自变量 在指数的位置上且为单个
(3)说明:为什么规定底数a大于0且不等于1?(1)(3)若a=1时,函数值y=1,没有研究的必要.练一练:下列函数是指数函数吗,为什么?在同一坐标系中分别作出如下函数的图像: 列表如下:2.指数函数的图象:观察右边图象,回答下列问题:问题一:
图象分别在哪几个象限?问题二:图象中有哪些特殊的点?
答:四个图象都经过点____.
问题三:图象的上升、下降与底数a有联系吗?
答:当底数__时图象上升;当底数____时图象下降.
答:四个图象都在第____象限Ⅰ、Ⅱ2.指数函数的图象3.根据指数函数的图象研究它的性质R(0,+∞)(0,1)增函数减函数当 x > 0 时,y > 1.
当 x < 0 时,. 0< y < 1
当 x < 0 时,y > 1;
当 x > 0 时, 0< y < 1。例2、比较下列各题中两个值的大小:(1)1.72.5与1.73(2)0.8-0.1与0.8-0.2 归纳: 两个同底的指数幂比较大小,可构造以该底数为底的指数函数再根据函数的单调性,比较指数的大小解(1)底数都是1.7 , ∴ 又∵2 .5<3,∵ 在R上是增函数 (2)可考查指数函数∴ 在R上是减函数∵ 0.8 <1又∵ ,故考查指数函数 ∴ < ∴ (4) (4)由指数函数的性质知: 1.70.3>1.7 0 =1 归纳:不同底的幂的大小比较,常可借用中间量1或0来比较。(3) 1.70.3与1解:(3)因为1=1.70,而由指数函数的性质知:函数 为增函数,而0.3>0,
故1.70.3 >1.70即1.70.3 > 1.0.93.1<0.90=1, 故: 1.70.3>0.93.1. 例3、(1)若 , 则m与n的大小如何?
解:(1)构造指数函数∵ 所以此函数为减函数又∵∴(2)构造函数∵∴此函数为增函数又∵∴即三、小结 想一想:这节课你收获到了什么?必做 P92, 练习A中1,2
选做 练习B中1,2,3四、作业本节课结束
