3.3 幂函数 课件(26张PPT)
文档属性
| 名称 | 3.3 幂函数 课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 21:42:49 | ||
图片预览







文档简介
课件26张PPT。第二章 基本初等函数
2.3 幂函数教学目标:
我们先来看几个具体的问题:以上问题中的函数具有什么共同特征??共同特征:
1、指数为常数;
2、均是以自变量为底的幂;
[定义:]一般地,函数 叫做幂函数 ,
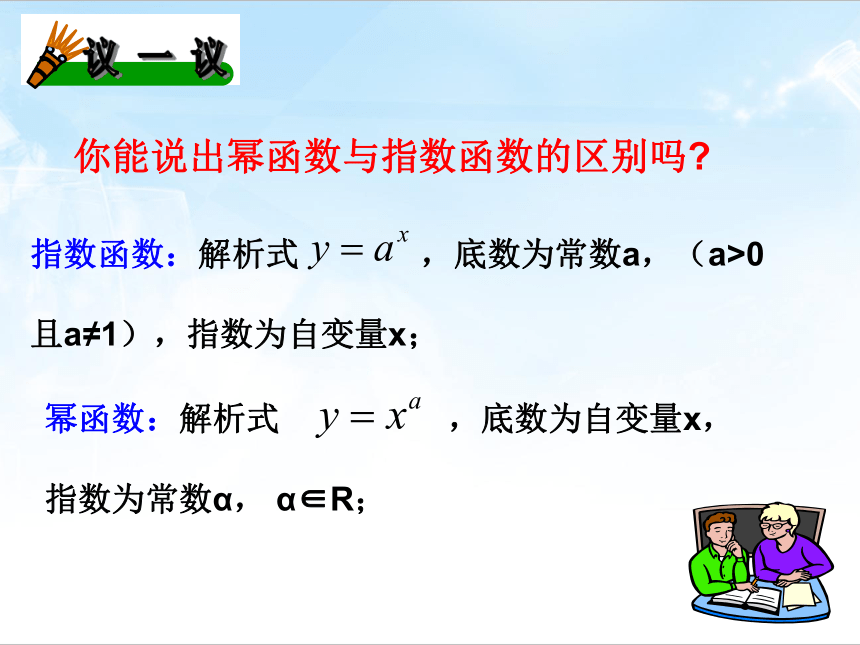
其中 为自变量, 为常数。注意:幂函数的解析式必须是 的形式, 其特征可归纳为“两个1:系数为1,只有1项”.你能说出幂函数与指数函数的区别吗?指数函数:解析式 ,底数为常数a,(a>0
且a≠1),指数为自变量x;幂函数:解析式 ,底数为自变量x,
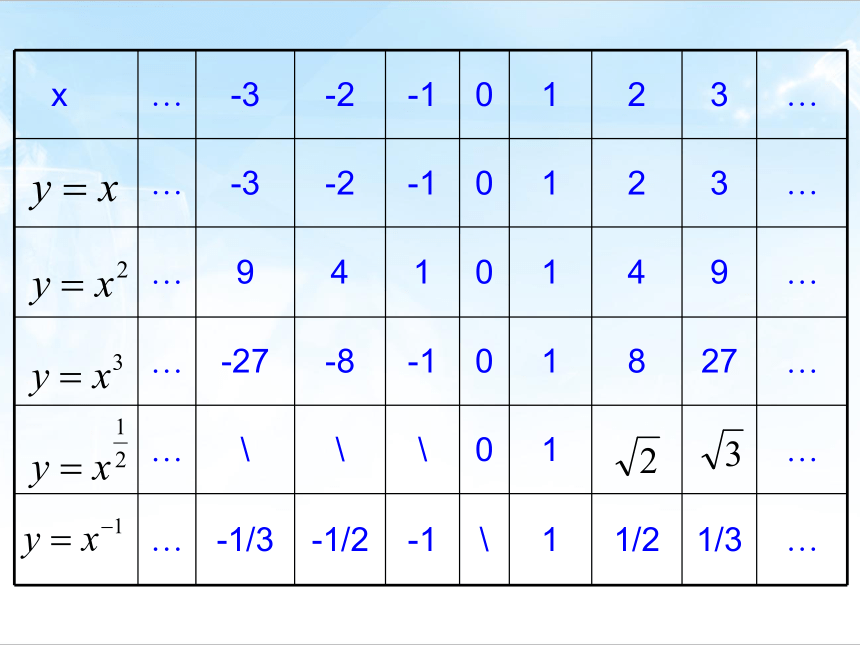
指数为常数α, α∈R;下面研究幂函数 的图象在同一平面直角坐标系内作出这五个幂函数的图象.
观察幂函数图象,将你发现的结论写在下表
RRRRR[0,+∞)[0,+∞)[0,+∞){x|x≠0}{y|y≠0}奇奇奇偶
非奇
非偶在 R上增在 R
上增在(-∞,0)
上减
在(0,+∞)
上减
在[ 0,+∞)
上增
(1,1)在(-∞,0 ]
上减
在[ 0,+∞)
上增
不管指数是多少,图象都经过哪个定点?图象都经过点(1,1)在第一象限内,函数图象的变化趋势与指数有什么关系?在第一象限内,
当a>0时,图象随x增大而上升。
当a<0时,图象随x增大而下降。
(1) 所有的幂函数在(0,+∞)都有定义,并且图象都通过点(1,1); (2) 如果α>0,则幂函数图象过原点,并且在区间[0,+∞)上是增函数; (3) 如果α<0,则幂函数图象在区间(0,+∞)上是减函数;幂函数的性质
例1 如果函数 是幂函数,且在区间(0,+∞)内是减函数,求满足条件的实数 的集合。解:依题意得
检验:当 时,函数为
符合题意;
当 时,函数为
不符合题意,舍去.
所以,
例2 证明幂函数 在[0,+∞)上是
增函数.证明:任取所以幂函数 在[0,+∞)上是增函数.1、下列结论正确的是( )
A.幂函数图象一定过原点
B.当α<0时,幂函数y=xα是减函数
C.当α>1时,幂函数y=xα是增函数
D.函数y=x2既是二次函数,也是幂函数答案: D2、利用单调性判断下列各值的大小3、求下列幂函数的定义域,并判断其奇偶性幂函数定义五个特殊幂函数图象基本性质本节知识结构:必做题:课本79页 习题2.3第 1、2两题。选做题:课本82页 复习参考题A组第10题。祝同学们学习进步
2.3 幂函数教学目标:
我们先来看几个具体的问题:以上问题中的函数具有什么共同特征??共同特征:
1、指数为常数;
2、均是以自变量为底的幂;
[定义:]一般地,函数 叫做幂函数 ,
其中 为自变量, 为常数。注意:幂函数的解析式必须是 的形式, 其特征可归纳为“两个1:系数为1,只有1项”.你能说出幂函数与指数函数的区别吗?指数函数:解析式 ,底数为常数a,(a>0
且a≠1),指数为自变量x;幂函数:解析式 ,底数为自变量x,
指数为常数α, α∈R;下面研究幂函数 的图象在同一平面直角坐标系内作出这五个幂函数的图象.
观察幂函数图象,将你发现的结论写在下表
RRRRR[0,+∞)[0,+∞)[0,+∞){x|x≠0}{y|y≠0}奇奇奇偶
非奇
非偶在 R上增在 R
上增在(-∞,0)
上减
在(0,+∞)
上减
在[ 0,+∞)
上增
(1,1)在(-∞,0 ]
上减
在[ 0,+∞)
上增
不管指数是多少,图象都经过哪个定点?图象都经过点(1,1)在第一象限内,函数图象的变化趋势与指数有什么关系?在第一象限内,
当a>0时,图象随x增大而上升。
当a<0时,图象随x增大而下降。
(1) 所有的幂函数在(0,+∞)都有定义,并且图象都通过点(1,1); (2) 如果α>0,则幂函数图象过原点,并且在区间[0,+∞)上是增函数; (3) 如果α<0,则幂函数图象在区间(0,+∞)上是减函数;幂函数的性质
例1 如果函数 是幂函数,且在区间(0,+∞)内是减函数,求满足条件的实数 的集合。解:依题意得
检验:当 时,函数为
符合题意;
当 时,函数为
不符合题意,舍去.
所以,
例2 证明幂函数 在[0,+∞)上是
增函数.证明:任取所以幂函数 在[0,+∞)上是增函数.1、下列结论正确的是( )
A.幂函数图象一定过原点
B.当α<0时,幂函数y=xα是减函数
C.当α>1时,幂函数y=xα是增函数
D.函数y=x2既是二次函数,也是幂函数答案: D2、利用单调性判断下列各值的大小3、求下列幂函数的定义域,并判断其奇偶性幂函数定义五个特殊幂函数图象基本性质本节知识结构:必做题:课本79页 习题2.3第 1、2两题。选做题:课本82页 复习参考题A组第10题。祝同学们学习进步
