2.1.3 函数的单调性 课件(22张PPT)
文档属性
| 名称 | 2.1.3 函数的单调性 课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 124.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 00:00:00 | ||
图片预览




文档简介
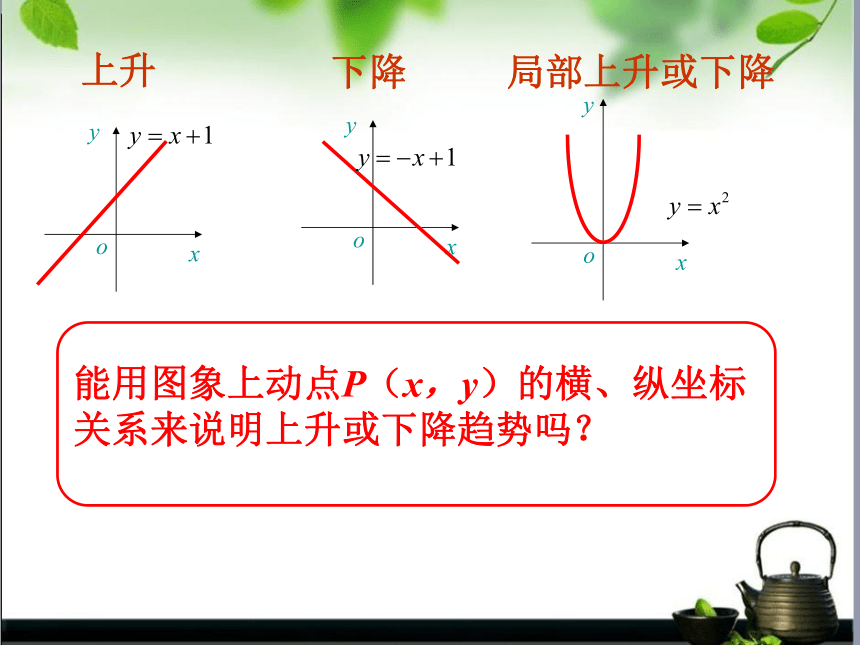
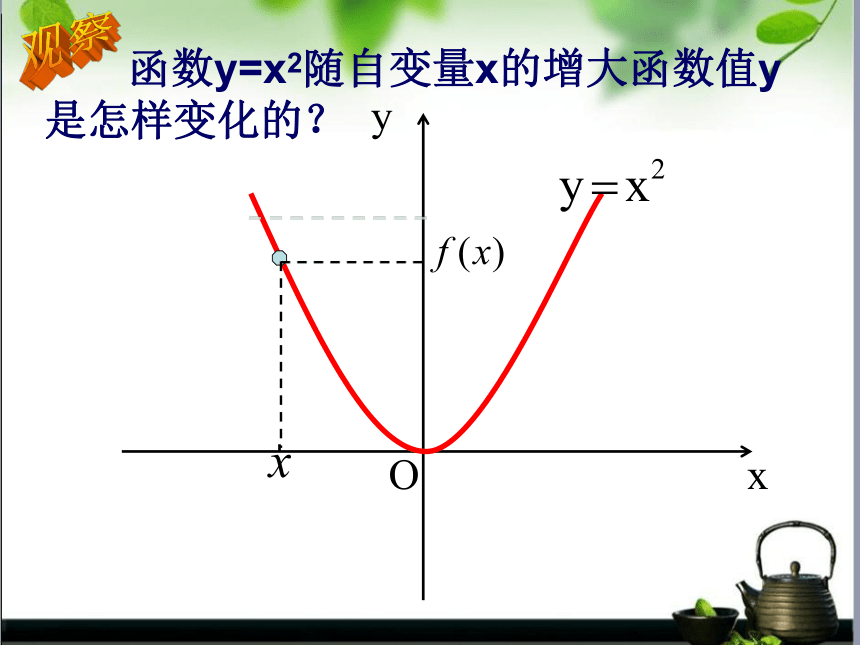
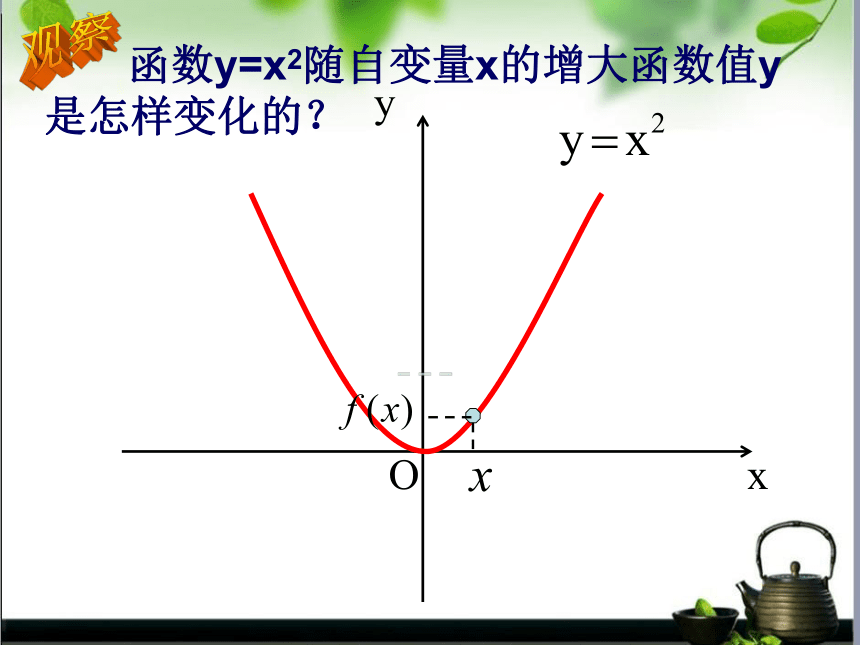
课件22张PPT。函数的单调性 某市一天24小时的气温变化图y=f(x),x∈[0,24]说出气温在哪些时间段内是逐渐升高或下降的?问题引入能用图象上动点P(x,y)的横、纵坐标关系来说明上升或下降趋势吗?局部上升或下降下降上升Oxy 函数y=x2随自变量x的增大函数值y
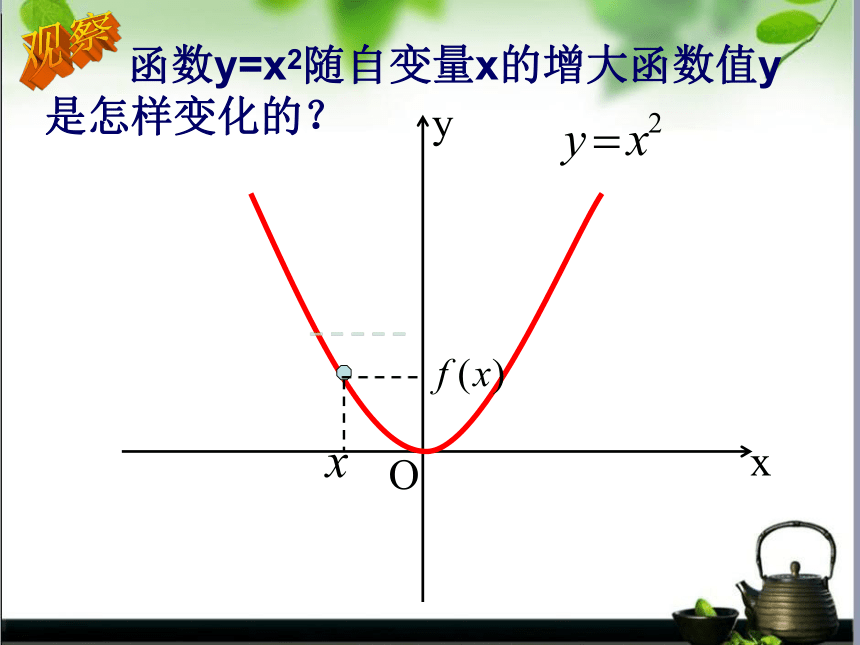
是怎样变化的?观察Oxy 函数y=x2随自变量x的增大函数值y
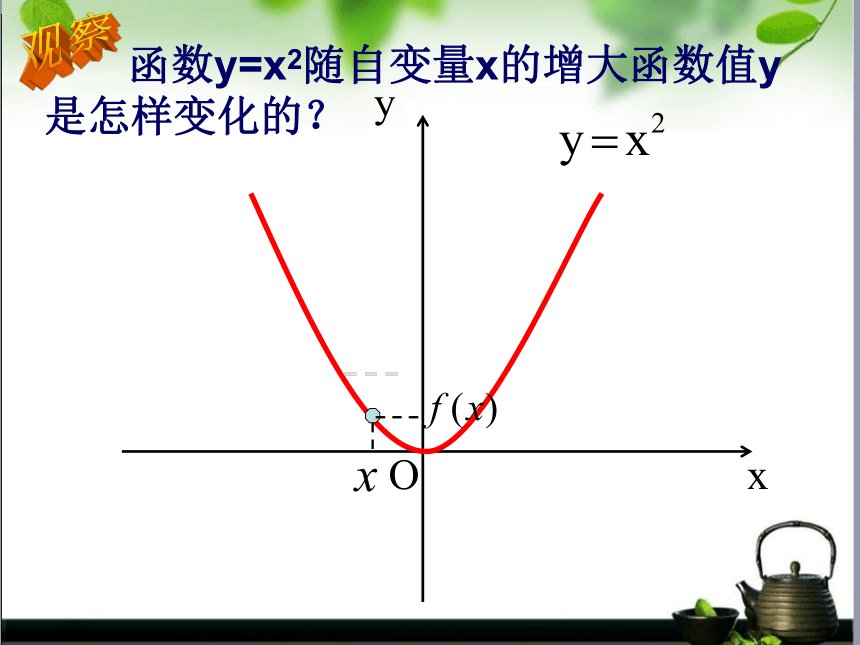
是怎样变化的?观察Oxy 函数y=x2随自变量x的增大函数值y
是怎样变化的?观察Oxy 函数y=x2随自变量x的增大函数值y
是怎样变化的?观察Oxy 函数y=x2随自变量x的增大函数值y
是怎样变化的?观察Oxy 函数y=x2随自变量x的增大函数值y
是怎样变化的?观察Oxy 函数y=x2随自变量x的增大函数值y
是怎样变化的?观察
当x的值增大时,函数值y也增大 图像在该区间内逐渐上升在某一区间内,当x的值增大时,函数值y却减小图像在该区间内逐渐下降函数为该区间上的增函数函数为该区间上的减函数探索发现通过之前的观察与研究,你能总结出增函数与减函数的定义吗?x 如果取区间M中的任意两个值x1,x2,
改变量 ,
则当 时,
就称函数y=f(x)在区间M上是增函数. 设函数y=f(x)的定义域为A,M A设函数y=f(x)的定义域为A,M A如果取区间M中的任意两个值x1,x2,
改变量 ,
则当 时,就称函数y=f(x)在区间M上是减函数. (1)函数单调性是针对某个区间而言的,是一个局部性质;注意:比如:函数 f (x)满足 f (2)> f(1),则函数 f (x)在R 上是增函数. (2) x 1, x 2 取值的任意性(×)例1、如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上, y=f(x)是增函数还是减函数。-5-2135f(x)[-5,-2)[-2,1)[1,3)[3,5]xyo强调: ①端点值的取舍
②单调区间之间用“,”或“和”
解:函数y=f(x)的单调区间有: [-5,-2), [-2,1),[1,3), [3,5]。
函数y=f(x)在 [-2,1), [3,5]为增函数;在 [-5,-2), [1,3)为减函数。
-5典例探究
题型一、用图像法找函数的单调区间典例探究
题型二、用定义法证明函数的单调性证明函数单调性的步骤有哪些?思考?典例探究
题型二、用定义法证明函数的单调性1、 指出下列函数的单调区间:
2、试用定义法证明函数 在区间
上是单调递增函数。练一练课堂小结请总结一下你这节课的收获下课!
是怎样变化的?观察Oxy 函数y=x2随自变量x的增大函数值y
是怎样变化的?观察Oxy 函数y=x2随自变量x的增大函数值y
是怎样变化的?观察Oxy 函数y=x2随自变量x的增大函数值y
是怎样变化的?观察Oxy 函数y=x2随自变量x的增大函数值y
是怎样变化的?观察Oxy 函数y=x2随自变量x的增大函数值y
是怎样变化的?观察Oxy 函数y=x2随自变量x的增大函数值y
是怎样变化的?观察
当x的值增大时,函数值y也增大 图像在该区间内逐渐上升在某一区间内,当x的值增大时,函数值y却减小图像在该区间内逐渐下降函数为该区间上的增函数函数为该区间上的减函数探索发现通过之前的观察与研究,你能总结出增函数与减函数的定义吗?x 如果取区间M中的任意两个值x1,x2,
改变量 ,
则当 时,
就称函数y=f(x)在区间M上是增函数. 设函数y=f(x)的定义域为A,M A设函数y=f(x)的定义域为A,M A如果取区间M中的任意两个值x1,x2,
改变量 ,
则当 时,就称函数y=f(x)在区间M上是减函数. (1)函数单调性是针对某个区间而言的,是一个局部性质;注意:比如:函数 f (x)满足 f (2)> f(1),则函数 f (x)在R 上是增函数. (2) x 1, x 2 取值的任意性(×)例1、如图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上, y=f(x)是增函数还是减函数。-5-2135f(x)[-5,-2)[-2,1)[1,3)[3,5]xyo强调: ①端点值的取舍
②单调区间之间用“,”或“和”
解:函数y=f(x)的单调区间有: [-5,-2), [-2,1),[1,3), [3,5]。
函数y=f(x)在 [-2,1), [3,5]为增函数;在 [-5,-2), [1,3)为减函数。
-5典例探究
题型一、用图像法找函数的单调区间典例探究
题型二、用定义法证明函数的单调性证明函数单调性的步骤有哪些?思考?典例探究
题型二、用定义法证明函数的单调性1、 指出下列函数的单调区间:
2、试用定义法证明函数 在区间
上是单调递增函数。练一练课堂小结请总结一下你这节课的收获下课!
