3.1.2 指数函数及其性质 课件(23张PPT)
文档属性
| 名称 | 3.1.2 指数函数及其性质 课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 15.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 21:39:54 | ||
图片预览







文档简介
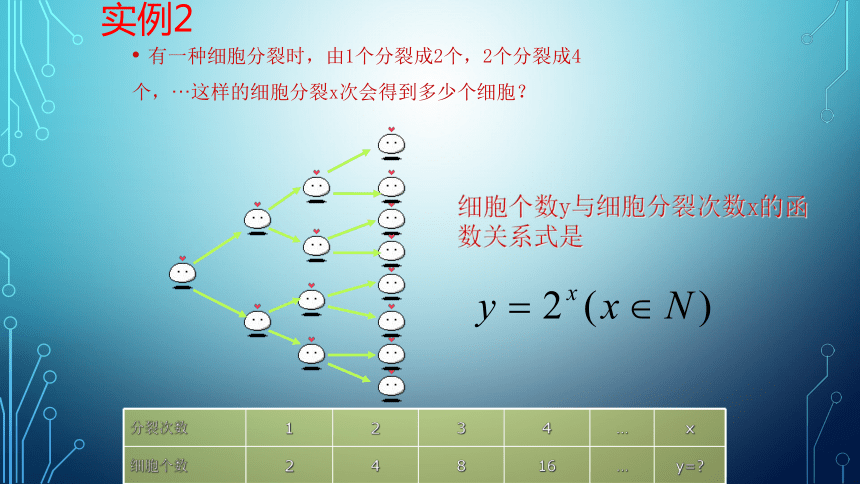
课件23张PPT。指数函数及其性质人教B版2003课标版学习目标掌握指数函数的概念、图像和性质通过自主探究,经历“特殊到一般到特殊”的认知过程,完善认知结构,领会数形结合、分类讨论、归纳推理等数学思想方法感受数学问题探索的乐趣和成功的喜悦,体会数学的理性、严谨及数与形的和谐统一美。 一种放射性物质随着时间而不断衰减,已知它经过一年剩留的质量约是原来的80%,请问:若有1克这种放射性物质,经过x年,剩留的质量y与x的函数关系是?实例1实例2有一种细胞分裂时,由1个分裂成2个,2个分裂成4
个,···这样的细胞分裂x次会得到多少个细胞?细胞个数y与细胞分裂次数x的函数关系式是实例3庄子曰:一尺之棰,日取其半,万世不竭。木棒长度y与经历天数x的
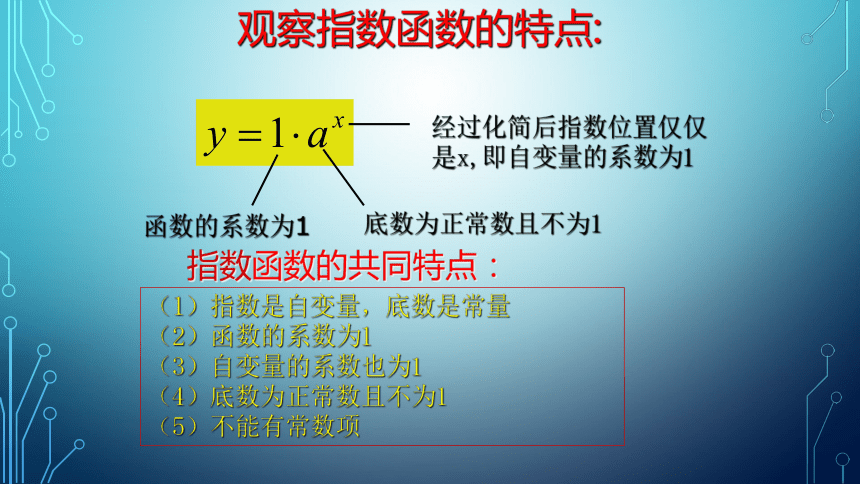
关系式是 一尺长的棍子,第一天剪掉其一半,第二天剪掉其剩余的一半……,若设剪了x次后剩余棍子的长度为y米,试写出y和x之间的关系第1次第2次第3次第4次第x次 一般地,函数y=ax (a>0,a≠1) 叫做指数函数,其中x是自变量,函数的定义域是R。 如果用字母a来代替2,1/2,0.8,那么以上三个函数都可以表示为形如y=ax的函数。观察指数函数的特点:函数的系数为1底数为正常数且不为1经过化简后指数位置仅仅是x,即自变量的系数为1(1)指数是自变量,底数是常量
(2)函数的系数为1
(3)自变量的系数也为1
(4)底数为正常数且不为1
(5)不能有常数项 指数函数的共同特点:(2)若a<0,则对于x的某些数值,可使ax无意义。 探究:为什么要规定a>0,且a≠1?(1)若a=0,当x≥0时, 当x<0时, (3)若a=1,则对于任何x∈R,总有ax=1,这时没有研究的必要性。 ax无意义 ax=0 下列函数中哪些是指数函数?(1) y=4x; (2) y=x4;(3) y=-4x; (4) y=(-4)x;(5) y=πx; (6) y=42x ;(7) y=xx; (8) y=(2a-1)x(a>1/2且a≠1);(1) (5) (6) (8)(2) (3) (4) (7)01122xy43-1-23-3作出函数图象: 1、定义域
2、对应关系
3、值域
4、定点
5、单调性
6、奇偶性自主探究:指数函数的性质?(3)在R上减函数(1)定义域为R,值域为(0,+ ∞ )(2)图像都过点(0,1),当x=0时,y=1(3)在R上增函数(4)当x>0时,y>1当x<0时,0<y<1(4)当x>0时, 0<y<1当x<0时, y>1例1、 比较下列各题中两数值的大小 ① 1.72.5,1.73.
② 0.8-0.1 ,0.8-0.2②因为指数函数y= 0.8x在R上是减函数. -0.1>-0.2 ∴0.8-0.1 < 0.8-0.2 解:① 因为指数函数y=1.7x 在R上是增函数. 2.5<3 所以 1.72.5<1.73 例题解析练习巩固:比较大小① 0.79-0.1 0.790.1
② 2.012.8 2.013.5
③ b2 b4(0④ a0.3与a0.4 (a>0 且a≠1)归纳:比较两个同底数幂的大小时,可以构造一个指数函数,再利用指数函数的单调性即可比较大小.><>例2、比较下列各题中两数值的大小 ① ( )0.4 与1 ②0.8-0.3 与4.9-0.1 归纳:比较两个不同底数幂的大小时,通常引入第三个数作参照. 解:①∵( )0.4>( )0=1 ∴( )0.4>1② ∵0.8-0.3>0.80=1 4.9-0.1<4.90=1
∴0.8-0.3 >4.9-0.1 例题解析练习巩固:比较大小 练习 2 比较大小
① 1.20.3 1 ② 0.3-5.1 1
③ ④>>>>例3 (1)已知下列不等式,比较m、n的大小。
① 2m<2n ②0.2m>0.2n
③ am>an (a≠1且a>1) 解:① m③当a>1时,m>n,当0例题解析练习3、求满足下列条件的x取值范围
① 23x+1 >
②( )x2-6x-16 <1
练习巩固 比较a 2x2+1与a x2+2 (a>0且a≠1)的大小?
课后思考函数
定义研究函数的一般方法是:函数
图像具体
函数函数
性质利用性质解决问题数学思想方法:由特殊到一般到特殊2. 指数函数的图像有哪些特征?3. 指数函数有哪些性质?4. 怎样用指数函数的性质比较两个幂的大小及求参数范围?1. 什么是 指数函数?课堂小结教材 课后习题A组题作业祝你进步!
个,···这样的细胞分裂x次会得到多少个细胞?细胞个数y与细胞分裂次数x的函数关系式是实例3庄子曰:一尺之棰,日取其半,万世不竭。木棒长度y与经历天数x的
关系式是 一尺长的棍子,第一天剪掉其一半,第二天剪掉其剩余的一半……,若设剪了x次后剩余棍子的长度为y米,试写出y和x之间的关系第1次第2次第3次第4次第x次 一般地,函数y=ax (a>0,a≠1) 叫做指数函数,其中x是自变量,函数的定义域是R。 如果用字母a来代替2,1/2,0.8,那么以上三个函数都可以表示为形如y=ax的函数。观察指数函数的特点:函数的系数为1底数为正常数且不为1经过化简后指数位置仅仅是x,即自变量的系数为1(1)指数是自变量,底数是常量
(2)函数的系数为1
(3)自变量的系数也为1
(4)底数为正常数且不为1
(5)不能有常数项 指数函数的共同特点:(2)若a<0,则对于x的某些数值,可使ax无意义。 探究:为什么要规定a>0,且a≠1?(1)若a=0,当x≥0时, 当x<0时, (3)若a=1,则对于任何x∈R,总有ax=1,这时没有研究的必要性。 ax无意义 ax=0 下列函数中哪些是指数函数?(1) y=4x; (2) y=x4;(3) y=-4x; (4) y=(-4)x;(5) y=πx; (6) y=42x ;(7) y=xx; (8) y=(2a-1)x(a>1/2且a≠1);(1) (5) (6) (8)(2) (3) (4) (7)01122xy43-1-23-3作出函数图象: 1、定义域
2、对应关系
3、值域
4、定点
5、单调性
6、奇偶性自主探究:指数函数的性质?(3)在R上减函数(1)定义域为R,值域为(0,+ ∞ )(2)图像都过点(0,1),当x=0时,y=1(3)在R上增函数(4)当x>0时,y>1当x<0时,0<y<1(4)当x>0时, 0<y<1当x<0时, y>1例1、 比较下列各题中两数值的大小 ① 1.72.5,1.73.
② 0.8-0.1 ,0.8-0.2②因为指数函数y= 0.8x在R上是减函数. -0.1>-0.2 ∴0.8-0.1 < 0.8-0.2 解:① 因为指数函数y=1.7x 在R上是增函数. 2.5<3 所以 1.72.5<1.73 例题解析练习巩固:比较大小① 0.79-0.1 0.790.1
② 2.012.8 2.013.5
③ b2 b4(0
∴0.8-0.3 >4.9-0.1 例题解析练习巩固:比较大小 练习 2 比较大小
① 1.20.3 1 ② 0.3-5.1 1
③ ④>>>>例3 (1)已知下列不等式,比较m、n的大小。
① 2m<2n ②0.2m>0.2n
③ am>an (a≠1且a>1) 解:① m
① 23x+1 >
②( )x2-6x-16 <1
练习巩固 比较a 2x2+1与a x2+2 (a>0且a≠1)的大小?
课后思考函数
定义研究函数的一般方法是:函数
图像具体
函数函数
性质利用性质解决问题数学思想方法:由特殊到一般到特殊2. 指数函数的图像有哪些特征?3. 指数函数有哪些性质?4. 怎样用指数函数的性质比较两个幂的大小及求参数范围?1. 什么是 指数函数?课堂小结教材 课后习题A组题作业祝你进步!
