6.2.1图形的认识 整理与复习 课件(25张ppt)
文档属性
| 名称 | 6.2.1图形的认识 整理与复习 课件(25张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 492.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-27 00:00:00 | ||
图片预览



文档简介
课件25张PPT。立体图形的
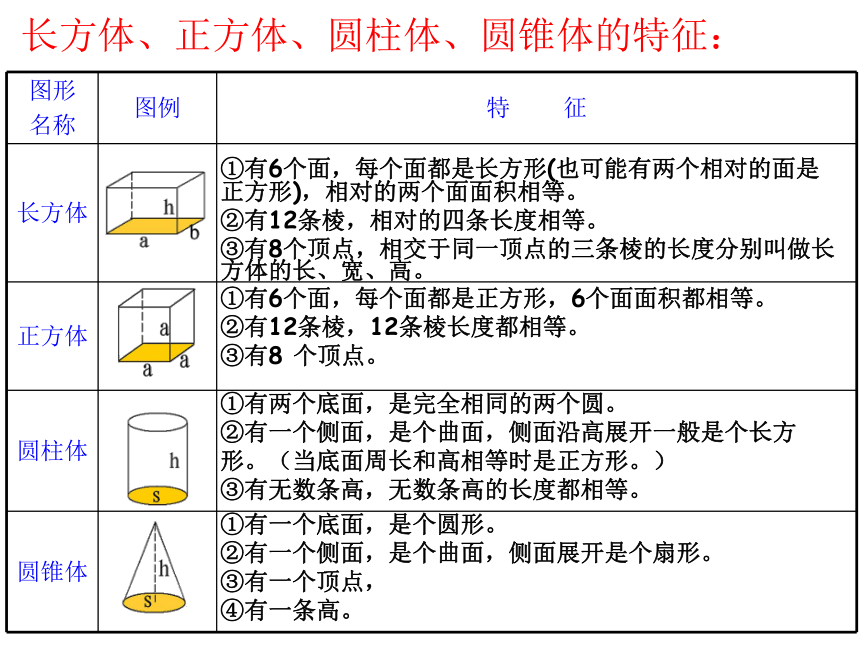
整理与复习长方体、正方体、圆柱体、圆锥体的特征:①有6个面,每个面都是长方形(也可能有两个相对的面是正方形),相对的两个面面积相等。
②有12条棱,相对的四条长度相等。
③有8个顶点,相交于同一顶点的三条棱的长度分别叫做长方体的长、宽、高。①有6个面,每个面都是正方形,6个面面积都相等。
②有12条棱,12条棱长度都相等。
③有8 个顶点。①有两个底面,是完全相同的两个圆。
②有一个侧面,是个曲面,侧面沿高展开一般是个长方形。(当底面周长和高相等时是正方形。)
③有无数条高,无数条高的长度都相等。①有一个底面,是个圆形。
②有一个侧面,是个曲面,侧面展开是个扇形。
③有一个顶点,
④有一条高。
复习提纲: (1)什么是物体的表面积?什么是物体的体积?什么是物体的容积?体积和容积有什么联系或区别?(从意义、测量方法、单位名称、计算方法几方面去考虑。)
(2)长方体正方体棱长总和、各个立体图形的表面积、体积公式是怎样的?它们的体积公式是怎样推导出来的?
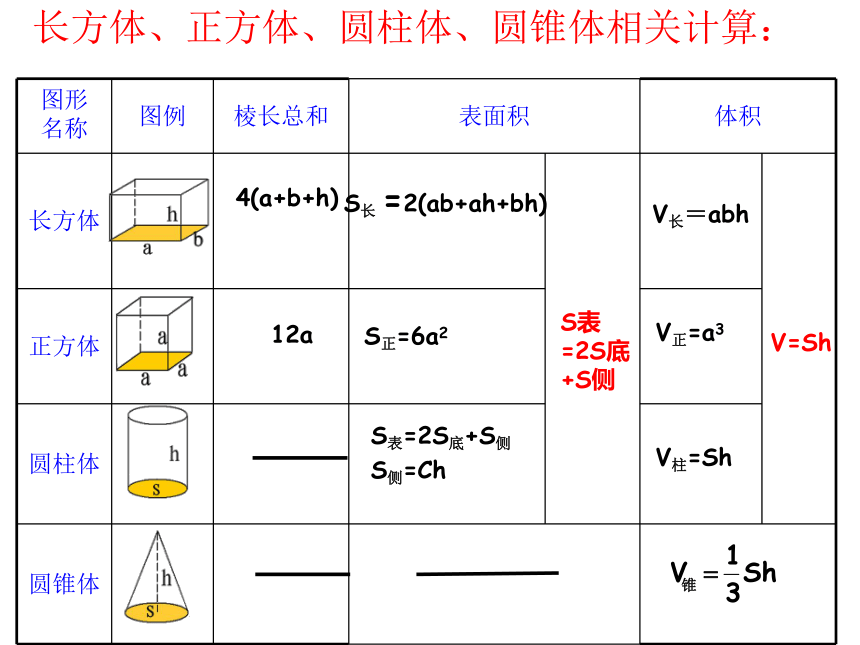
(3)在解决有关立体图形的表面积和体积的问题时,需要特别提醒自己(或同学)注意什么?长方体、正方体、圆柱体、圆锥体相关计算: 4(a+b+h)S长 =2(ab+ah+bh)
S正=6a2S表=2S底+S侧
S侧=Ch
V长=abh12aV正=a3 V柱=ShV=ShS表=2S底+S侧复习提纲: (1)什么是物体的表面积?什么是物体的体积?什么是物体的容积?体积和容积有什么联系或区别?(从意义、测量方法、单位名称、计算方法几方面去考虑。)
(2)长方体正方体棱长总和、各个立体图形的表面积、体积公式是怎样的?它们的体积公式是怎样推导出来的?
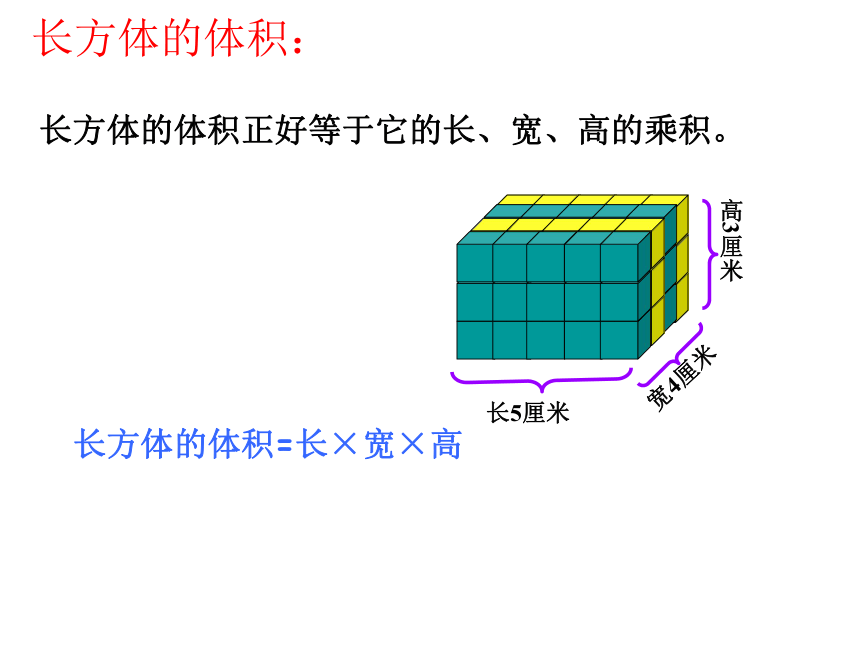
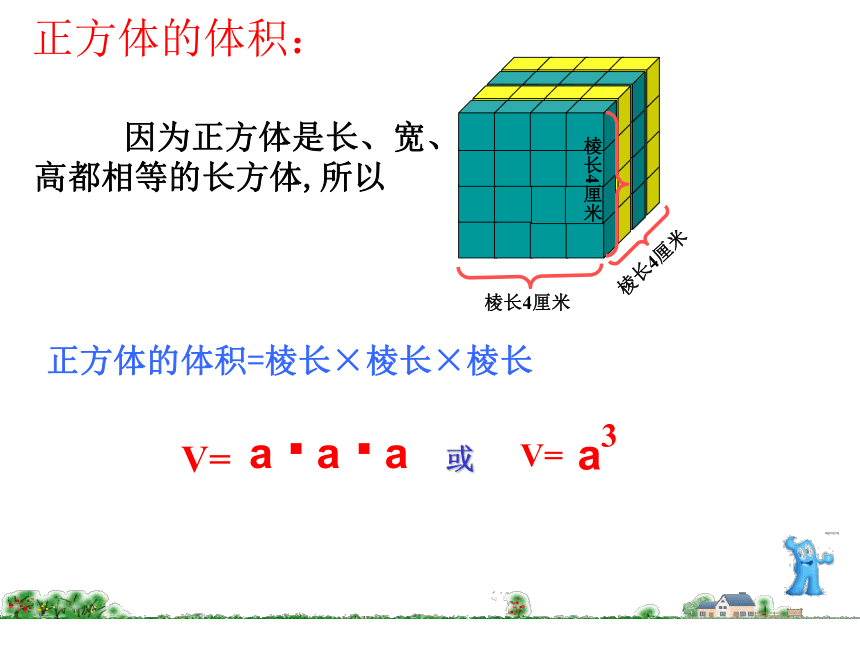
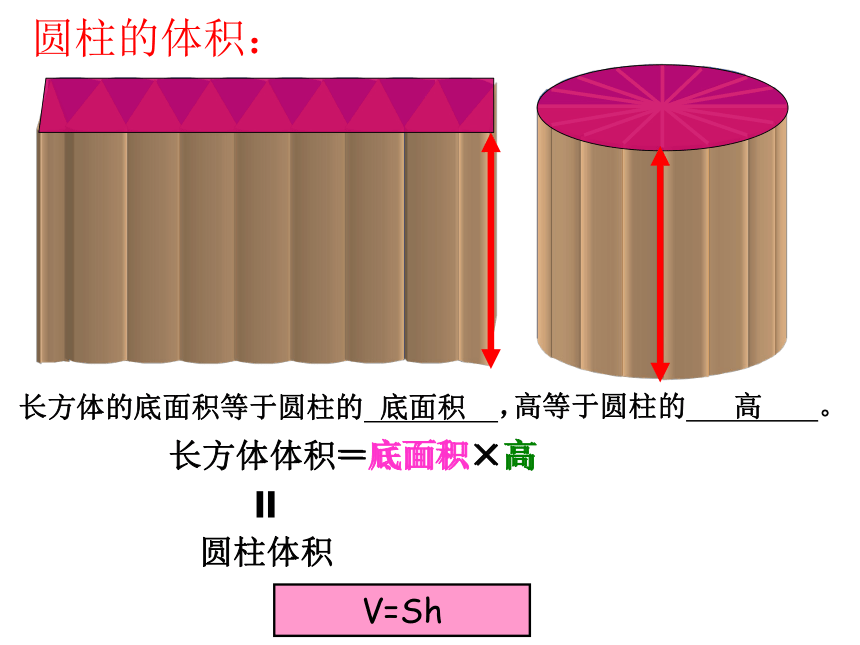
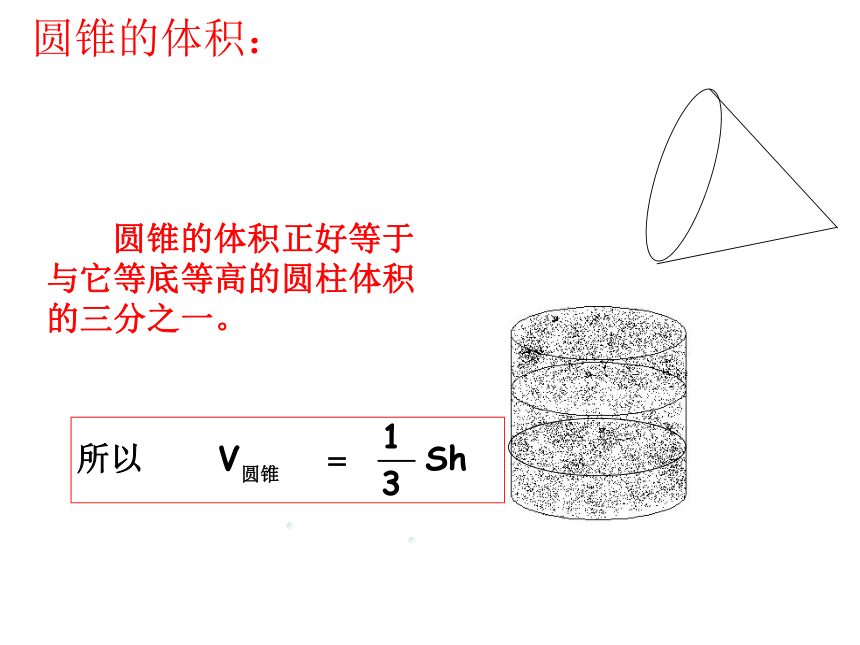
(3)在解决有关立体图形的表面积和体积的问题时,需要特别提醒自己(或同学)注意什么?长5厘米宽4厘米高3厘米长方体的体积正好等于它的长、宽、高的乘积。长方体的体积=长×宽×高长方体的体积:棱长4厘米棱长4厘米棱长4厘米 因为正方体是长、宽、高都相等的长方体,所以正方体的体积=棱长×棱长×棱长或正方体的体积:长方体体积=底面积×高圆柱体积==底面积×高长方体的底面积等于圆柱的 底面积 , 高等于圆柱的 高 。 V=Sh圆柱的体积: 圆锥的体积正好等于与它等底等高的圆柱体积的三分之一。圆锥的体积:复习提纲: (1)什么是物体的表面积?什么是物体的体积?什么是物体的容积?体积和容积有什么联系或区别?(从意义、测量方法、单位名称、计算方法几方面去考虑。)
(2)长方体正方体棱长总和、各个立体图形的表面积、体积公式是怎样的?它们的体积公式是怎样推导出来的?
(3)在解决有关立体图形的表面积和体积的问题时,需要特别提醒自己(或同学)注意什么?√× 1、等底等高的长方体、正方体、圆柱体的体积也一定相等。( )
2、圆锥的体积是圆柱体积的 。( )
3、一个圆柱形杯子的体积等于它的容积。( )
4、 求做一个圆柱形的通风管需要多少铁皮,就是求
圆柱的表面积 ( )
5、棱长是6厘米的正方体,它的体积和它的表面积一样大 。( ) 辨一辨: × × × 1、把一个圆柱的底面平均分成若干个扇形,然后切开拼成一个近似的长方体。下面哪句话是正确的?( )
A、表面积和体积都没变化。
B、表面积和体积都发生了变化。
C、表面积变了,体积没变。
D、表面积没变,体积变了。
C 选择: A、54 B、18 C 、0.6 D、6 2、等底等体积的圆柱和圆锥,圆锥的高是18厘米,那么圆柱的高是( )厘米。D 选择: 3、等高等体积的圆柱和圆锥,圆柱的底面积是6平方厘米,那么圆锥的底面积是( )平方厘米。A、6 B、18
C、2 D、36
B 选择: 4、把一个底面半径是2分米、高是3分米的圆柱形容器中注满水,现垂直轻轻插入一根底面积是5平方分米,高是4分米的方钢,溢出水的体积是( )毫升。
A、20 B、15 C、20000 D、15000D 选择: 回答下面的问题,并列出算式(不计算):
1、一个圆柱形无盖的水桶,底面半径10分米,高20分米。
(1)给这个水桶加个箍,是求什么?
(2)求这个水桶的占地面积,是求什么?
(3)做这样一个水桶用多少铁皮,是求什么?
(4)这个水桶能装多少水,是求什么?
2×3.14×103.14×1023.14×102+2×3.14×10×203.14×102×20 基本练习: 2、做一个圆柱形的油箱,底面半径3分米,高4分米。至少需要铁皮多少平方分米?
3、做一个无盖圆柱形的水桶,底面直径6分米,高4分米。至少需要铁皮多少平方分米?
4、做一节圆柱形的通风管,底面周长18.84分米,长4分米。至少需要铁皮多少平方分米?18.84 × 43.14 ×32×2 + 2×3.14×3×4 基本练习: 4、新建的篮球馆要铺设3cm厚的木质地板,已知该馆的长36m,宽20m,铺设它至少需要用多少方木材? 3mm=0.03m
36×20×0.03
=720×0.03
=21.6(m3)
答:铺设它至少需要用21.6m3木材。 基本练习: 6、把两个棱长是4厘米的正方体木块粘合成一个长方体,这个长方体的表面积是多少平方厘米?方法三、4×4×10=160(平方厘米)方法一、(8×4+8×4+4×4)×2=160(平方厘米)方法四、4×4×12- 4×4×2=160(平方厘米)方法二、8×4×4 + 4×4×2=160(平方厘米) 基本练习: (1)从角上拿一个,它的体积表面积是怎样变化的? 拓展练习: (2)现在它的体积和表面积发生怎样的变化? 拓展练习: (3)从中间拿掉一个,它的体积和表面积发生怎样的变化? 拓展练习: 5、一个圆柱形木材,沿着一条底面直径纵向剖开,量得一个纵剖面面积是6平方分米,那么,圆柱的侧面积是多少平方分米?3.14×6=18.84(平方分米) 拓展练习: 6、一个长方体,它的底面积是40平方米,底面周长是26米,高是5米,求它的表面积是多少? 26×5+40×2
=130+80
=210(m2)
答:它的表面积是210m2。 基本练习: 拓展练习: 7、一个长圆柱体,把它截成两个小圆柱,表面积增加80平方米。把它切成两个半圆柱表面积增加60平方米,求它的表面积是多少? 80+60÷2×3.14
=80+94.2
=174.2(m2)
答:它的表面积是174.2m2。 基本练习: 拓展练习:
②有12条棱,相对的四条长度相等。
③有8个顶点,相交于同一顶点的三条棱的长度分别叫做长方体的长、宽、高。①有6个面,每个面都是正方形,6个面面积都相等。
②有12条棱,12条棱长度都相等。
③有8 个顶点。①有两个底面,是完全相同的两个圆。
②有一个侧面,是个曲面,侧面沿高展开一般是个长方形。(当底面周长和高相等时是正方形。)
③有无数条高,无数条高的长度都相等。①有一个底面,是个圆形。
②有一个侧面,是个曲面,侧面展开是个扇形。
③有一个顶点,
④有一条高。
复习提纲: (1)什么是物体的表面积?什么是物体的体积?什么是物体的容积?体积和容积有什么联系或区别?(从意义、测量方法、单位名称、计算方法几方面去考虑。)
(2)长方体正方体棱长总和、各个立体图形的表面积、体积公式是怎样的?它们的体积公式是怎样推导出来的?
(3)在解决有关立体图形的表面积和体积的问题时,需要特别提醒自己(或同学)注意什么?长方体、正方体、圆柱体、圆锥体相关计算: 4(a+b+h)S长 =2(ab+ah+bh)
S正=6a2S表=2S底+S侧
S侧=Ch
V长=abh12aV正=a3 V柱=ShV=ShS表=2S底+S侧复习提纲: (1)什么是物体的表面积?什么是物体的体积?什么是物体的容积?体积和容积有什么联系或区别?(从意义、测量方法、单位名称、计算方法几方面去考虑。)
(2)长方体正方体棱长总和、各个立体图形的表面积、体积公式是怎样的?它们的体积公式是怎样推导出来的?
(3)在解决有关立体图形的表面积和体积的问题时,需要特别提醒自己(或同学)注意什么?长5厘米宽4厘米高3厘米长方体的体积正好等于它的长、宽、高的乘积。长方体的体积=长×宽×高长方体的体积:棱长4厘米棱长4厘米棱长4厘米 因为正方体是长、宽、高都相等的长方体,所以正方体的体积=棱长×棱长×棱长或正方体的体积:长方体体积=底面积×高圆柱体积==底面积×高长方体的底面积等于圆柱的 底面积 , 高等于圆柱的 高 。 V=Sh圆柱的体积: 圆锥的体积正好等于与它等底等高的圆柱体积的三分之一。圆锥的体积:复习提纲: (1)什么是物体的表面积?什么是物体的体积?什么是物体的容积?体积和容积有什么联系或区别?(从意义、测量方法、单位名称、计算方法几方面去考虑。)
(2)长方体正方体棱长总和、各个立体图形的表面积、体积公式是怎样的?它们的体积公式是怎样推导出来的?
(3)在解决有关立体图形的表面积和体积的问题时,需要特别提醒自己(或同学)注意什么?√× 1、等底等高的长方体、正方体、圆柱体的体积也一定相等。( )
2、圆锥的体积是圆柱体积的 。( )
3、一个圆柱形杯子的体积等于它的容积。( )
4、 求做一个圆柱形的通风管需要多少铁皮,就是求
圆柱的表面积 ( )
5、棱长是6厘米的正方体,它的体积和它的表面积一样大 。( ) 辨一辨: × × × 1、把一个圆柱的底面平均分成若干个扇形,然后切开拼成一个近似的长方体。下面哪句话是正确的?( )
A、表面积和体积都没变化。
B、表面积和体积都发生了变化。
C、表面积变了,体积没变。
D、表面积没变,体积变了。
C 选择: A、54 B、18 C 、0.6 D、6 2、等底等体积的圆柱和圆锥,圆锥的高是18厘米,那么圆柱的高是( )厘米。D 选择: 3、等高等体积的圆柱和圆锥,圆柱的底面积是6平方厘米,那么圆锥的底面积是( )平方厘米。A、6 B、18
C、2 D、36
B 选择: 4、把一个底面半径是2分米、高是3分米的圆柱形容器中注满水,现垂直轻轻插入一根底面积是5平方分米,高是4分米的方钢,溢出水的体积是( )毫升。
A、20 B、15 C、20000 D、15000D 选择: 回答下面的问题,并列出算式(不计算):
1、一个圆柱形无盖的水桶,底面半径10分米,高20分米。
(1)给这个水桶加个箍,是求什么?
(2)求这个水桶的占地面积,是求什么?
(3)做这样一个水桶用多少铁皮,是求什么?
(4)这个水桶能装多少水,是求什么?
2×3.14×103.14×1023.14×102+2×3.14×10×203.14×102×20 基本练习: 2、做一个圆柱形的油箱,底面半径3分米,高4分米。至少需要铁皮多少平方分米?
3、做一个无盖圆柱形的水桶,底面直径6分米,高4分米。至少需要铁皮多少平方分米?
4、做一节圆柱形的通风管,底面周长18.84分米,长4分米。至少需要铁皮多少平方分米?18.84 × 43.14 ×32×2 + 2×3.14×3×4 基本练习: 4、新建的篮球馆要铺设3cm厚的木质地板,已知该馆的长36m,宽20m,铺设它至少需要用多少方木材? 3mm=0.03m
36×20×0.03
=720×0.03
=21.6(m3)
答:铺设它至少需要用21.6m3木材。 基本练习: 6、把两个棱长是4厘米的正方体木块粘合成一个长方体,这个长方体的表面积是多少平方厘米?方法三、4×4×10=160(平方厘米)方法一、(8×4+8×4+4×4)×2=160(平方厘米)方法四、4×4×12- 4×4×2=160(平方厘米)方法二、8×4×4 + 4×4×2=160(平方厘米) 基本练习: (1)从角上拿一个,它的体积表面积是怎样变化的? 拓展练习: (2)现在它的体积和表面积发生怎样的变化? 拓展练习: (3)从中间拿掉一个,它的体积和表面积发生怎样的变化? 拓展练习: 5、一个圆柱形木材,沿着一条底面直径纵向剖开,量得一个纵剖面面积是6平方分米,那么,圆柱的侧面积是多少平方分米?3.14×6=18.84(平方分米) 拓展练习: 6、一个长方体,它的底面积是40平方米,底面周长是26米,高是5米,求它的表面积是多少? 26×5+40×2
=130+80
=210(m2)
答:它的表面积是210m2。 基本练习: 拓展练习: 7、一个长圆柱体,把它截成两个小圆柱,表面积增加80平方米。把它切成两个半圆柱表面积增加60平方米,求它的表面积是多少? 80+60÷2×3.14
=80+94.2
=174.2(m2)
答:它的表面积是174.2m2。 基本练习: 拓展练习:
