人教版A版选修4—4 2.2.1 圆锥曲线的参数方程-椭圆(共15张ppt)
文档属性
| 名称 | 人教版A版选修4—4 2.2.1 圆锥曲线的参数方程-椭圆(共15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 795.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-26 16:41:36 | ||
图片预览





文档简介
课件15张PPT。
圆锥曲线的参数方程
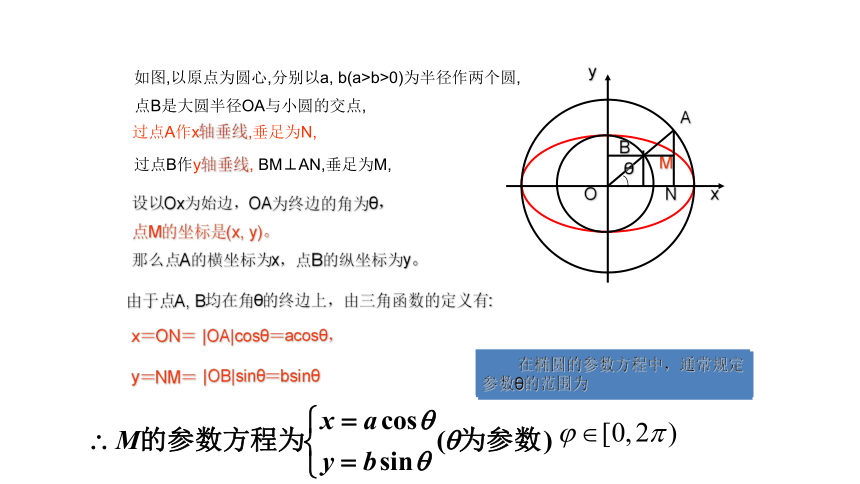
圆锥曲线的参数方程(椭圆)一、知识回顾问题2:你能仿此推导出椭圆 的参数方程吗?这就是椭圆的参数方程M如图,以原点为圆心,分别以a, b(a>b>0)为半径作两个圆,点B是大圆半径OA与小圆的交点,过点A作x轴垂线,垂足为N,过点B作y轴垂线, BM⊥AN,垂足为M,ANB
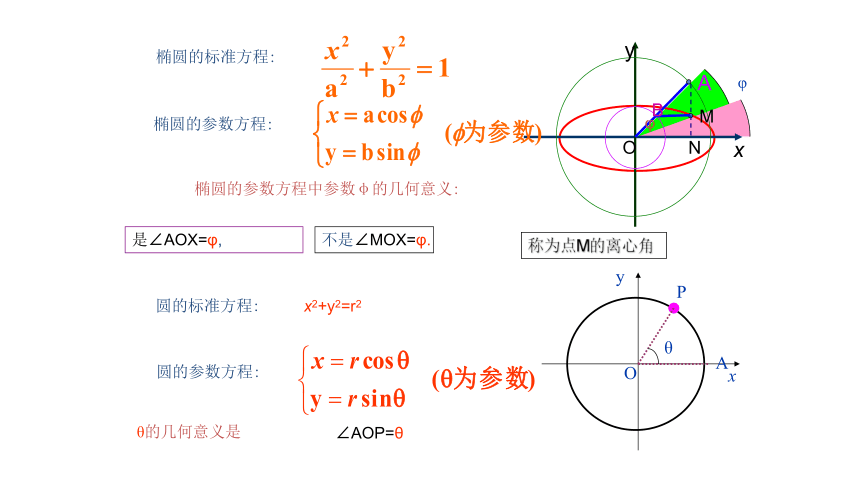
设以Ox为始边,OA为终边的角为θ,点M的坐标是(x, y)。那么点A的横坐标为x,点B的纵坐标为y。由于点A, B均在角θ的终边上,由三角函数的定义有:y=NM=x=ON= 这是中心在原点O,焦点在x轴上的椭圆的参数方程。 常数a、b分别是椭圆的长半轴长和短半轴长。 在椭圆的参数方程中,通常规定参数θ的范围为|OA|cosθ=acosθ,|OB|sinθ=bsinθθ椭圆的标准方程:椭圆的参数方程中参数φ的几何意义:圆的标准方程:圆的参数方程: x2+y2=r2θ的几何意义是∠AOP=θ椭圆的参数方程:是∠AOX=φ, 不是∠MOX=φ.称为点M的离心角 φ【练习1】把下列普通方程化为参数方程. 把下列参数方程化为普通方程例1、如图,在椭圆x2/9+y2/4=1上求一点P,使P到直线 l:2x-3y-10=0的距离最小.分析1平移直线 l 至首次与椭圆相切,切点即为所求.小结:借助椭圆的参数方程,可以将椭圆上的任意一点的坐标用三角函数表示,利用三角知识加以解决。分析2=解:设椭圆内接矩形的一个顶点坐标为所以椭圆内接矩形面积的最大值为2ab.练习3:已知A,B两点是椭圆 与坐标轴正半轴的两个交点,在第一象限的椭圆弧上求一点P,使四边形OAPB的面积最大.即求点P到线AB的距离最大值线AB的方程为:2x+3y-6=0=所以当d有最大值,面积最大这时点P的坐标为三、课堂小结(1)椭圆的参数方程与应用注意:椭圆参数与圆的参数方程中参数的几何意义不同。(2)椭圆与直线相交问题
圆锥曲线的参数方程
圆锥曲线的参数方程(椭圆)一、知识回顾问题2:你能仿此推导出椭圆 的参数方程吗?这就是椭圆的参数方程M如图,以原点为圆心,分别以a, b(a>b>0)为半径作两个圆,点B是大圆半径OA与小圆的交点,过点A作x轴垂线,垂足为N,过点B作y轴垂线, BM⊥AN,垂足为M,ANB
设以Ox为始边,OA为终边的角为θ,点M的坐标是(x, y)。那么点A的横坐标为x,点B的纵坐标为y。由于点A, B均在角θ的终边上,由三角函数的定义有:y=NM=x=ON= 这是中心在原点O,焦点在x轴上的椭圆的参数方程。 常数a、b分别是椭圆的长半轴长和短半轴长。 在椭圆的参数方程中,通常规定参数θ的范围为|OA|cosθ=acosθ,|OB|sinθ=bsinθθ椭圆的标准方程:椭圆的参数方程中参数φ的几何意义:圆的标准方程:圆的参数方程: x2+y2=r2θ的几何意义是∠AOP=θ椭圆的参数方程:是∠AOX=φ, 不是∠MOX=φ.称为点M的离心角 φ【练习1】把下列普通方程化为参数方程. 把下列参数方程化为普通方程例1、如图,在椭圆x2/9+y2/4=1上求一点P,使P到直线 l:2x-3y-10=0的距离最小.分析1平移直线 l 至首次与椭圆相切,切点即为所求.小结:借助椭圆的参数方程,可以将椭圆上的任意一点的坐标用三角函数表示,利用三角知识加以解决。分析2=解:设椭圆内接矩形的一个顶点坐标为所以椭圆内接矩形面积的最大值为2ab.练习3:已知A,B两点是椭圆 与坐标轴正半轴的两个交点,在第一象限的椭圆弧上求一点P,使四边形OAPB的面积最大.即求点P到线AB的距离最大值线AB的方程为:2x+3y-6=0=所以当d有最大值,面积最大这时点P的坐标为三、课堂小结(1)椭圆的参数方程与应用注意:椭圆参数与圆的参数方程中参数的几何意义不同。(2)椭圆与直线相交问题
