人教A版数学选修2—2 1.1.3 导数的几何意义(共18张ppt)
文档属性
| 名称 | 人教A版数学选修2—2 1.1.3 导数的几何意义(共18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 770.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-26 00:00:00 | ||
图片预览





文档简介
课件18张PPT。导数及其应用1.1.3 导数的几何意义 定义:函数y=f(x)在x=x0处的瞬时变化率是
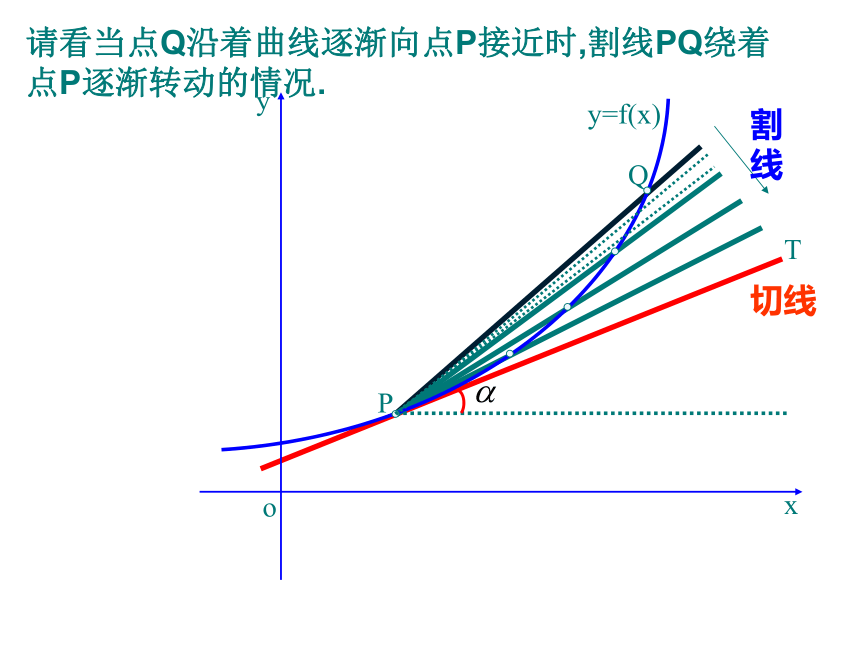
我们称它为函数y=f(x)在x=x0处的导数,记作:知识回顾 由导数的意义可知,求函数y=f(x)在点x0处的导数的基本方法是:下面来看导数的几何意义: 如图,曲线C是函数y=f(x)
的图象,P(x0,y0)是曲线C上的
任意一点,Q(x0+Δx,y0+Δy)
为P邻近一点,PQ为C的割线,
PM//x轴,QM//y轴,β为PQ的
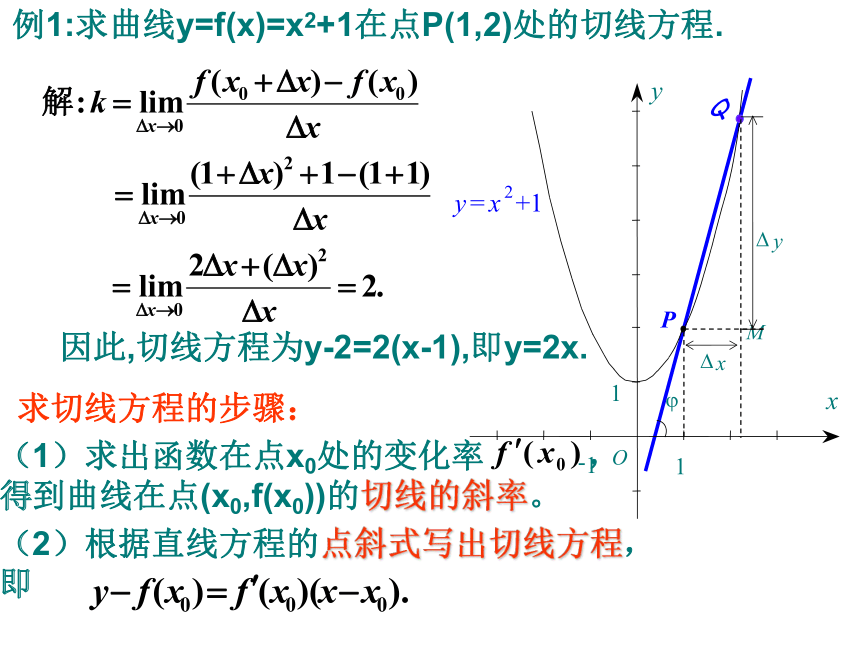
倾斜角.斜率!PQ割线切线T请看当点Q沿着曲线逐渐向点P接近时,割线PQ绕着点P逐渐转动的情况. 我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ有一个确定位置PT.则我们把直线PT称为曲线在点P处的切线. 设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率.即: 这个概念:①提供了求曲线上某点切线的斜率的一种方法;②切线斜率的本质——函数在x=x0处的导数.导数的几何意义 函数 y=f(x)在点x0处的导数的几何意义,就是曲线 y=f(x)在点P(x0 ,f(x0))处的切线的斜率.即: 故曲线y=f(x)在点P(x0 ,f(x0))处的切线方程是:因此,切线方程为y-2=2(x-1),即y=2x.(1)求出函数在点x0处的变化率 ,
得到曲线在点(x0,f(x0))的切线的斜率。(2)根据直线方程的点斜式写出切线方程,
即求切线方程的步骤:即点P处的切线的斜率等于4. (2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.在不致发生混淆时,导函数也简称导数.什么是导函数?从求函数f(x)在x=x0处导数的过程可以看到,当x=x0时,f’(x0) 是一个确定的数.那么,当x变化时, f’(x0)便是x的一个函数,我们叫它为f(x)的导函数.即:1.已知曲线y=f(x)=2x2上一点A(2,8),则点A处的切线斜率为(
)
A.4 B.16 C.8 D.2c2.已知曲线y=f(x)=2x2+4x在点P处的切线斜率为16.则P点坐标为________.令4x0+4=16得x0=3,∴P(3,30).(3,30)3.求抛物线y=x2过点 的切线方程.解:设切点为(x0, x02),则x0=2,3,k=4,6切线方程为:y=4x-4,y=6x-9知识小结:1.导数的几何意义2.求切线方程的一般步骤
(注意在某点;过某点区别)3.导函数与导数的区别求曲线y=f(x)过点P(x0,f(x0))的切线方程的五个步骤设切点设切点为(m,f(m))求导数求f ′(m),即切线的斜率导数几何意义 --数学因探索而精彩
--数学因应用而美丽
我们称它为函数y=f(x)在x=x0处的导数,记作:知识回顾 由导数的意义可知,求函数y=f(x)在点x0处的导数的基本方法是:下面来看导数的几何意义: 如图,曲线C是函数y=f(x)
的图象,P(x0,y0)是曲线C上的
任意一点,Q(x0+Δx,y0+Δy)
为P邻近一点,PQ为C的割线,
PM//x轴,QM//y轴,β为PQ的
倾斜角.斜率!PQ割线切线T请看当点Q沿着曲线逐渐向点P接近时,割线PQ绕着点P逐渐转动的情况. 我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ有一个确定位置PT.则我们把直线PT称为曲线在点P处的切线. 设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率.即: 这个概念:①提供了求曲线上某点切线的斜率的一种方法;②切线斜率的本质——函数在x=x0处的导数.导数的几何意义 函数 y=f(x)在点x0处的导数的几何意义,就是曲线 y=f(x)在点P(x0 ,f(x0))处的切线的斜率.即: 故曲线y=f(x)在点P(x0 ,f(x0))处的切线方程是:因此,切线方程为y-2=2(x-1),即y=2x.(1)求出函数在点x0处的变化率 ,
得到曲线在点(x0,f(x0))的切线的斜率。(2)根据直线方程的点斜式写出切线方程,
即求切线方程的步骤:即点P处的切线的斜率等于4. (2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.在不致发生混淆时,导函数也简称导数.什么是导函数?从求函数f(x)在x=x0处导数的过程可以看到,当x=x0时,f’(x0) 是一个确定的数.那么,当x变化时, f’(x0)便是x的一个函数,我们叫它为f(x)的导函数.即:1.已知曲线y=f(x)=2x2上一点A(2,8),则点A处的切线斜率为(
)
A.4 B.16 C.8 D.2c2.已知曲线y=f(x)=2x2+4x在点P处的切线斜率为16.则P点坐标为________.令4x0+4=16得x0=3,∴P(3,30).(3,30)3.求抛物线y=x2过点 的切线方程.解:设切点为(x0, x02),则x0=2,3,k=4,6切线方程为:y=4x-4,y=6x-9知识小结:1.导数的几何意义2.求切线方程的一般步骤
(注意在某点;过某点区别)3.导函数与导数的区别求曲线y=f(x)过点P(x0,f(x0))的切线方程的五个步骤设切点设切点为(m,f(m))求导数求f ′(m),即切线的斜率导数几何意义 --数学因探索而精彩
--数学因应用而美丽
