人教A版数学选修2—3 1.2.2 组合(共21张ppt)
文档属性
| 名称 | 人教A版数学选修2—3 1.2.2 组合(共21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 279.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-26 00:00:00 | ||
图片预览







文档简介
课件21张PPT。组合 问题一:从甲、乙、丙3名同学中选出2名去参加某天的一项活动,其中1名同学参加上午的活动,1名同学参加下午的活动,有多少种不同的选法?问题二:从甲、乙、丙3名同学中选出2名去参加某天一项活动,有多少种不同的选法?甲、乙;甲、丙;乙、丙 3 一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.组合及组合数的定义:如:从 a , b , c三个不同的元素中取出两个元素的所有组合个数是:如:已知4个元素a 、b 、 c 、 d ,取出两个元素的所有组合个数是:概念讲解组合定义: 一般地,从n个不同元素中取出m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.排列定义: 一般地,从n个不同元素中取出m (m≤n) 个元素,按照一定的顺序排成一列,叫做从 n 个不同元素中取出 m 个元素的一个排列.共同点: 都要“从n个不同元素中任取m个元素” 不同点: 排列与元素的顺序有关,
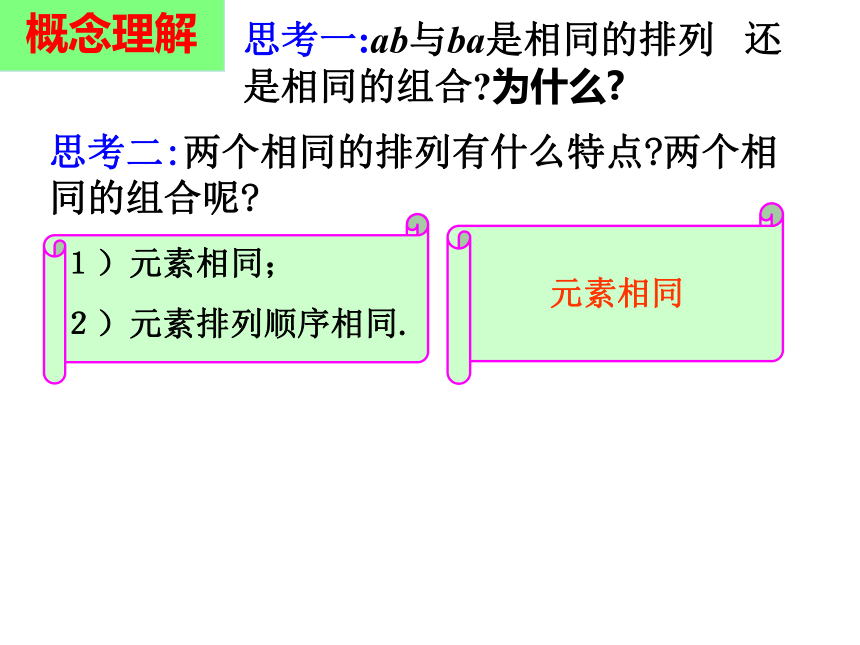
而组合则与元素的顺序无关.概念讲解思考一:ab与ba是相同的排列 还是相同的组合?为什么?思考二:两个相同的排列有什么特点?两个相同的组合呢?概念理解判断下列问题是组合问题还是排列问题? (1)设集合A={a,b,c,d,e},则集合A的含有3个元素的子集有多少个?(2)某铁路线上有5个车站,则这条铁路线上共需准备多少种车票? 有多少种不同的火车票价?组合问题排列问题组合问题组合是选择的结果,排列
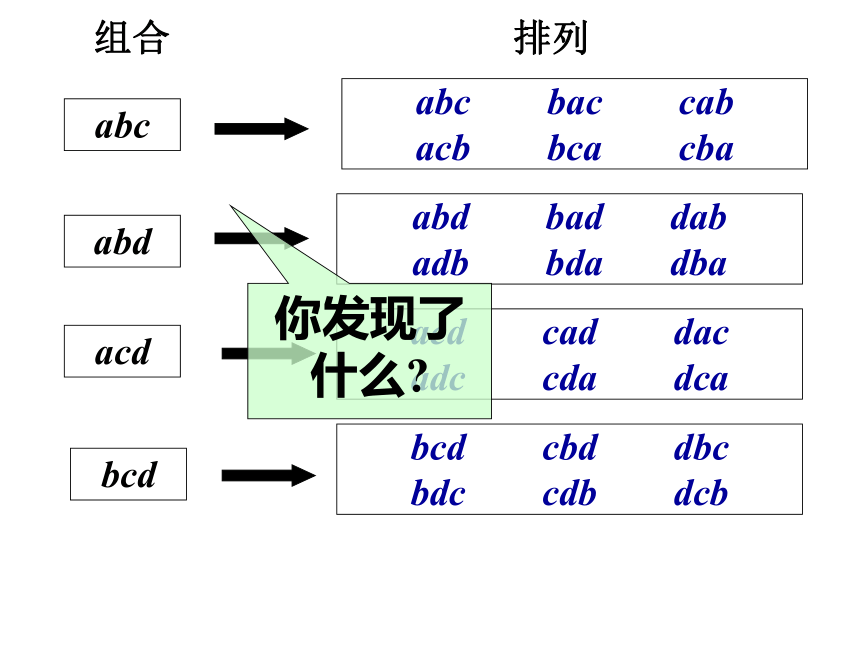
是选择后再排序的结果.写出从a,b,c,d 四个元素中任取三个元素的所有排列思考三:组合与排列有联系吗?组合排列abc bac cab
acb bca cba你发现了什么?组合数公式:从 n个不同元中取出m个元素的排列数概念讲解 例1 一位教练的足球队共有17名初级学员,他们中以前没有一人参加过比赛,按照足球比赛规则,比赛时一个足球队的上场队员是11人.问:简单的组合问题 (1)这位教练从这17名学员中可以形成多少种学员上场方案? (2)如果在选出11名上场队员时,还要确定其中的守门员,那么教练员有多少种方式做这件事情?(2)分两步完成这件事第1步,从17名学员中选出11人上场第2步,从上场的11人中选1名守门员例题讲解例2 (1)平面内有10个点,以其中每2个点为端点的线段共有多少条?10个不同元素中取2个元素的组合数. 10个不同元素中取2个元素的排列数. (2)平面内有10个点,以其中每2个点为端点的有向线段共有多少条?例题讲解 例3:在100件产品中,有98件合格品,2件次品.从这100件产品中任意抽出3件(1)有多少种不同的抽法?100个不同元素中取3个元素的组合数(2)抽出的3件中恰好有1件是次品的抽法有多少种?从2件次品中抽出1件次品的抽法有从98件合格品中抽出2件的抽法有 例3: 在100件产品中,有98件合格品,2件次品.从这100件产品中任意抽出3件(3)抽出的3件中至少有1件是次品的抽法有多少种?法1含1件次品或含2件次品法2100件中抽3件减98件合格品中抽3件某医院有内科医生8名,外科医生6名,现要派5人参加支边医疗队,至少要有1名内科医生和1名外科医生参加,有多少种选法?变式练习例4.一个口袋内装有大小不同的7个白球和1个黑球.(1)从口袋内取出3个球,使其中含有1个黑球,有多少种取法?(2)从口袋内取出3个球,使其中不含黑球,有多少种取法? (3)从口袋内取出3个球,共有多少种取法?解:(1)取出3个球中有黑球的方法数例题讲解例4.一个口袋内装有大小不同的7个白球和1个黑球.(1)从口袋内取出3个球,使其中含有1个黑球,有多少种取法?(2)从口袋内取出3个球,使其中不含黑球,有多少种取法? (3)从口袋内取出3个球,共有多少种取法?解:(1)取出3个球中有黑球的方法数⑵取出3个球中无黑球的方法数例题讲解例4.一个口袋内装有大小不同的7个白球和1个黑球.(1)从口袋内取出3个球,使其中含有1个黑球,有多少种取法?(2)从口袋内取出3个球,使其中不含黑球,有多少种取法? (3)从口袋内取出3个球,共有多少种取法?解:(3)按照黑球分类,②取出3个球中有黑球的方法数∴从口袋内取出3个球,共有取法①取出3个球中无黑球的方法数组合数的两个性质:
①性质(2)特征:下标相同而上标差1的两个组合数之和,等于下标比原下标多1而上标与大的相同的一个组合数; ③性质的作用:恒等变形,简化运算;②性质(2)体现:“含与不含某元素”的分类思想. 课堂小结2.组合数性质:1.组合数公式:2、4名男生6名女生,一共9名实习生分配到高一的
四个班级担任见习班主任,每班至少有男、女
实习生各1名的不同分配方案共有多少种?
课后作业:1、课外活动小组共13人,其中男生8人,女生5人,并且男、女各指定一名队长,现从中选5人主持某种活动,依下列条件各有多少种选法?
(1)只有一名女生;
(2)两队长当选;
(3)至少有一名队长当选;
(4)至多有两名女生当选;
(5)既要有队长,又要有女生当选.
而组合则与元素的顺序无关.概念讲解思考一:ab与ba是相同的排列 还是相同的组合?为什么?思考二:两个相同的排列有什么特点?两个相同的组合呢?概念理解判断下列问题是组合问题还是排列问题? (1)设集合A={a,b,c,d,e},则集合A的含有3个元素的子集有多少个?(2)某铁路线上有5个车站,则这条铁路线上共需准备多少种车票? 有多少种不同的火车票价?组合问题排列问题组合问题组合是选择的结果,排列
是选择后再排序的结果.写出从a,b,c,d 四个元素中任取三个元素的所有排列思考三:组合与排列有联系吗?组合排列abc bac cab
acb bca cba你发现了什么?组合数公式:从 n个不同元中取出m个元素的排列数概念讲解 例1 一位教练的足球队共有17名初级学员,他们中以前没有一人参加过比赛,按照足球比赛规则,比赛时一个足球队的上场队员是11人.问:简单的组合问题 (1)这位教练从这17名学员中可以形成多少种学员上场方案? (2)如果在选出11名上场队员时,还要确定其中的守门员,那么教练员有多少种方式做这件事情?(2)分两步完成这件事第1步,从17名学员中选出11人上场第2步,从上场的11人中选1名守门员例题讲解例2 (1)平面内有10个点,以其中每2个点为端点的线段共有多少条?10个不同元素中取2个元素的组合数. 10个不同元素中取2个元素的排列数. (2)平面内有10个点,以其中每2个点为端点的有向线段共有多少条?例题讲解 例3:在100件产品中,有98件合格品,2件次品.从这100件产品中任意抽出3件(1)有多少种不同的抽法?100个不同元素中取3个元素的组合数(2)抽出的3件中恰好有1件是次品的抽法有多少种?从2件次品中抽出1件次品的抽法有从98件合格品中抽出2件的抽法有 例3: 在100件产品中,有98件合格品,2件次品.从这100件产品中任意抽出3件(3)抽出的3件中至少有1件是次品的抽法有多少种?法1含1件次品或含2件次品法2100件中抽3件减98件合格品中抽3件某医院有内科医生8名,外科医生6名,现要派5人参加支边医疗队,至少要有1名内科医生和1名外科医生参加,有多少种选法?变式练习例4.一个口袋内装有大小不同的7个白球和1个黑球.(1)从口袋内取出3个球,使其中含有1个黑球,有多少种取法?(2)从口袋内取出3个球,使其中不含黑球,有多少种取法? (3)从口袋内取出3个球,共有多少种取法?解:(1)取出3个球中有黑球的方法数例题讲解例4.一个口袋内装有大小不同的7个白球和1个黑球.(1)从口袋内取出3个球,使其中含有1个黑球,有多少种取法?(2)从口袋内取出3个球,使其中不含黑球,有多少种取法? (3)从口袋内取出3个球,共有多少种取法?解:(1)取出3个球中有黑球的方法数⑵取出3个球中无黑球的方法数例题讲解例4.一个口袋内装有大小不同的7个白球和1个黑球.(1)从口袋内取出3个球,使其中含有1个黑球,有多少种取法?(2)从口袋内取出3个球,使其中不含黑球,有多少种取法? (3)从口袋内取出3个球,共有多少种取法?解:(3)按照黑球分类,②取出3个球中有黑球的方法数∴从口袋内取出3个球,共有取法①取出3个球中无黑球的方法数组合数的两个性质:
①性质(2)特征:下标相同而上标差1的两个组合数之和,等于下标比原下标多1而上标与大的相同的一个组合数; ③性质的作用:恒等变形,简化运算;②性质(2)体现:“含与不含某元素”的分类思想. 课堂小结2.组合数性质:1.组合数公式:2、4名男生6名女生,一共9名实习生分配到高一的
四个班级担任见习班主任,每班至少有男、女
实习生各1名的不同分配方案共有多少种?
课后作业:1、课外活动小组共13人,其中男生8人,女生5人,并且男、女各指定一名队长,现从中选5人主持某种活动,依下列条件各有多少种选法?
(1)只有一名女生;
(2)两队长当选;
(3)至少有一名队长当选;
(4)至多有两名女生当选;
(5)既要有队长,又要有女生当选.
