1.3 正方形的性质与判定 教案(2课时)
文档属性
| 名称 | 1.3 正方形的性质与判定 教案(2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 165.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-26 00:00:00 | ||
图片预览


文档简介
3 正方形的性质与判定
第1课时 正方形的性质
一、基本目标
1.了解正方形的有关概念,理解并掌握正方形的性质定理.
2.经历探索正方形有关性质的过程,在观察中寻求新知,在探究中发展推理能力,逐步掌握说理的基本方法.
二、重难点目标
【教学重点】
探索正方形的性质定理.
【教学难点】
掌握正方形的性质的应用方法.
三、教学过程
环节1 自学提纲、生成问题
【5 min阅读】
阅读教材P20~P21的内容,完成下面练习.
【3 min反馈】
正方形的性质:
(1)边:四条边都相等且对边平行.
(2)角:四个角都是直角.
(3)对角线:两条对角线互相垂直平分且相等,并且每一条对角线平分一组对角.
(4)正方形既是中心对称图形,又是轴对称图形,正方形有四条对称轴.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】如图,在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF.BE与DF之间有怎样的关系?请说明理由.
【互动探索】(引发学生思考)先用观察法,结合图形直观地猜测出BE与DF之间的关系,再利用已知条件,对猜测进行证明.
【解答】BE=DF且BE⊥DF.
理由:如题图,延长BE交DF于点M.
∵四边形ABCD是正方形,
∴BC=DC,∠BCE=90°,
∴∠DCF=180°-∠BCE=180°-90°=90°,
∴∠BCE=∠DCF.
又∵CE=CF,∴△BCE≌△DCF,
∴BE=DF,∠CBF=∠CDF.
∵∠DCF=90°,∴∠CDF+∠F=90°,
∴∠CBE+∠F=90°,
∴∠BMF=90°,∴BE⊥DF.
【互动总结】(学生总结,老师点评)本题是通过证明△BCE≌△DCF来得到BE与DF之间的关系,证明三角形全等是解决这一类型问题的常用做法.
活动2 巩固练习(学生独学)
1.正方形面积为36,则对角线的长为( B )
A.6 B.6
C.9 D.9
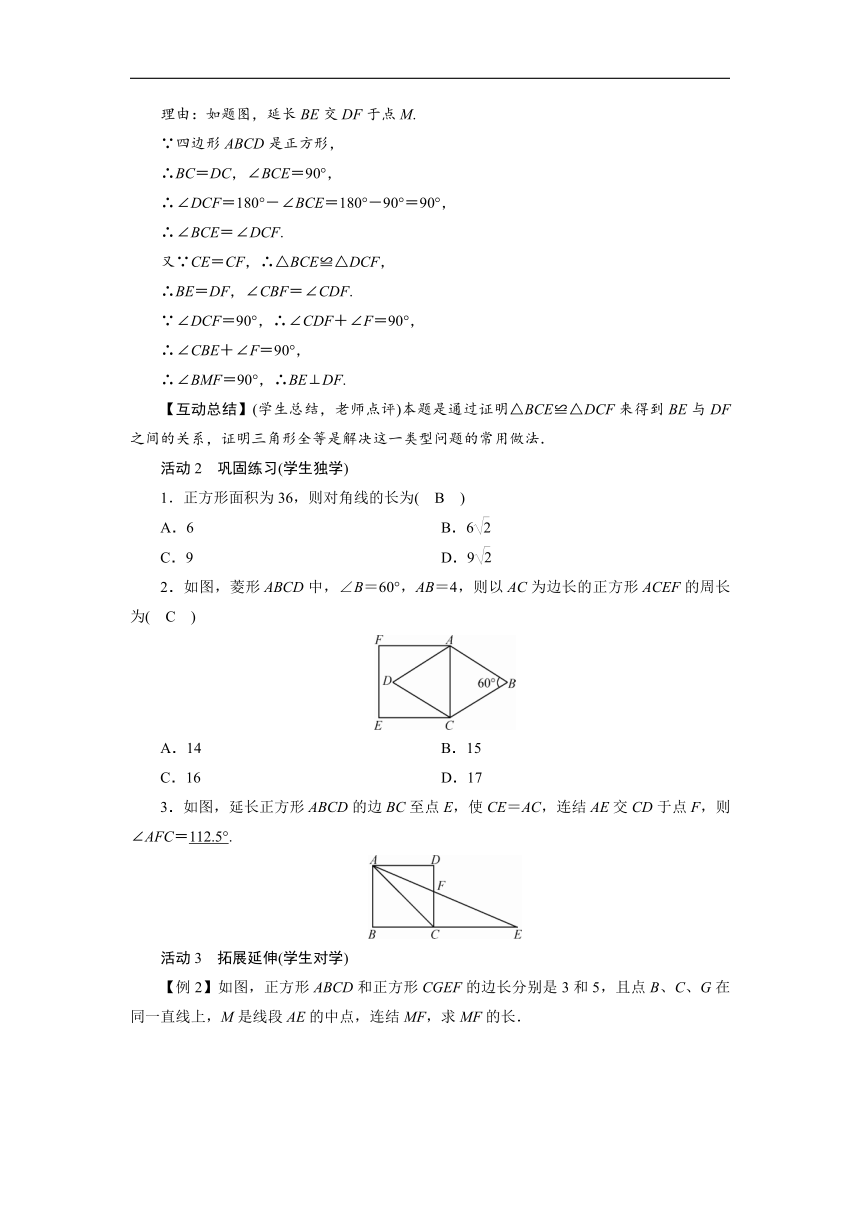
2.如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为( C )
A.14 B.15
C.16 D.17
3.如图,延长正方形ABCD的边BC至点E,使CE=AC,连结AE交CD于点F,则∠AFC=112.5°.
活动3 拓展延伸(学生对学)
【例2】如图,正方形ABCD和正方形CGEF的边长分别是3和5,且点B、C、G在同一直线上,M是线段AE的中点,连结MF,求MF的长.
【互动探索】结合已知条件,需作出辅助线,即连结DM并延长交EF于点N,再得到哪两个三角形全等,就可以解决问题?
【解答】连结DM并延长交EF于点N,如图.
∵四边形ABCD,四边形EFCG都是正方形,
∴AD∥BG,EF∥BG,∴EF∥AD,
∴∠NEM=∠DAM.
在△ADM和△ENM中,
∴△ADM≌△ENM,
∴AD=NE=3,DM=MN.
∵EF=5,∴FN=2.
∵DF=FC-CD=2,∴FN=FD,
∴FM是等腰直角△DFN的底边上的中线,所以FM=DN=.
【互动总结】(学生总结,老师点评)正确作出辅助线,结合正方形的性质,构造出全等三角形是解决本题的关键.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
正方形的性质
第2课时 正方形的判定
一、基本目标
1.掌握正方形的判定方法,会运用平行四边形、矩形、菱形、正方形的判定条件进行有关的论证和计算.
2.经历探究正方形判定条件的过程,发展学生初步的综合推理能力,主动探究的学习习惯,逐步掌握说理的基本方法.
二、重难点目标
【教学重点】
掌握正方形的判定条件.
【教学难点】
合理恰当地利用特殊平行四边形的判定进行有关的论证和计算.
三、教学过程
环节1 自学提纲、生成问题
【5 min阅读】
阅读教材P22~P24的内容,完成下面练习.
【3 min反馈】
1.正方形的判定:对角线相等的菱形是正方形;对角线垂直的矩形是正方形;有一个角是直角的菱形是正方形.
2.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是( C )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
【互动探索】(引发学生思考)由BF∥CE,CF∥BE,可直接得出四边形BECF是哪种特殊四边形?再结合矩形ABCD的性质,又能得出四边形BECF是哪种特殊四边形?
【证明】∵BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴∠ABC=90°,∠DCB=90°.
又∵BE平分∠ABC,CE平分∠DCB,
∴∠EBC=∠ABC=45°,
∠ECB=∠DCB=45°,
∴∠EBC=∠ECB,
∴EB=EC,∴平行四边形BECF是菱形.
在△EBC中,∵∠EBC=45°,∠ECB=45°,
∴∠BEC=90°,∴菱形BECF是正方形.
【互动总结】(学生总结,老师点评)掌握平行四边形、矩形、菱形成为正方形所需要的条件是解决这类问题的关键.
活动2 巩固练习(学生独学)
1.如图,在△ABC中,∠ABC=90°,BD平分∠ABC,DE⊥BC,DF⊥AB,垂足分别为E、F,求证:四边形BEDF是正方形.
证明:∵∠ABC=90°,DE⊥BC,DF⊥AB,∴四边形BEDF是矩形.∵BD平分∠ABC,DE⊥BC,DF⊥AB,∴DE=DF,∴四边形BEDF是正方形.
2.如图,点E、F、G、H分别是CD、BC、AB、DA的中点,求证:四边形EFGH是平行四边形.
证明:连结BD.∵点E、F、G、H分别是CD、BC、AB、DA的中点,∴EF是△BCD的中位线,GH是△ABD的中位线.∴EF∥BD,EF=BD,GH∥BD,GH=BD.∴EF∥GH,且EF=GH.∴四边形EFGH是平行四边形.
活动3 拓展延伸 (学生对学)
【例2】如图,已知E是正方形ABCD的对角线BD上的点,连结AE、CE.
(1)求证:AE=CE;
(2)若将△ABE沿AB翻折后得到△ABF,当点E在BD的何处时,四边形AFBE是正方形?请证明你的结论.
【互动探索】(1)结合已知条件和图形,要证AE=CE,只需证明哪两个三角形全等?(2)由折叠的性质得出哪些结论?
【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=CB,∠BAD=∠ABC=90°,∠ABE=∠CBE=45°,
在△ABE和△CBE中,
∴△ABE≌△CBE(SAS),
∴AE=CE.
(2)点E在BD的中点时,四边形AFBE是正方形.理由:
由折叠的性质,得∠F=∠AEB,AF=AE,BF=BE.
∵∠BAD=90°,AB=AD,E是BD的中点,
∴AE=BD=BE,∠AEB=90°,
∴AE=BE=AF=BF,
∴四边形AFBE是菱形.
又∵∠AEB=90°,
∴四边形AFBE是正方形.
【互动总结】(学生总结,老师点评)图形翻折前后,对应边相等,对应角相等,结合特殊平行四边形的性质与判定、全等三角形的性质求解此类题型.
环节3 课堂小结,当堂达标
第1课时 正方形的性质
一、基本目标
1.了解正方形的有关概念,理解并掌握正方形的性质定理.
2.经历探索正方形有关性质的过程,在观察中寻求新知,在探究中发展推理能力,逐步掌握说理的基本方法.
二、重难点目标
【教学重点】
探索正方形的性质定理.
【教学难点】
掌握正方形的性质的应用方法.
三、教学过程
环节1 自学提纲、生成问题
【5 min阅读】
阅读教材P20~P21的内容,完成下面练习.
【3 min反馈】
正方形的性质:
(1)边:四条边都相等且对边平行.
(2)角:四个角都是直角.
(3)对角线:两条对角线互相垂直平分且相等,并且每一条对角线平分一组对角.
(4)正方形既是中心对称图形,又是轴对称图形,正方形有四条对称轴.
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】如图,在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF.BE与DF之间有怎样的关系?请说明理由.
【互动探索】(引发学生思考)先用观察法,结合图形直观地猜测出BE与DF之间的关系,再利用已知条件,对猜测进行证明.
【解答】BE=DF且BE⊥DF.
理由:如题图,延长BE交DF于点M.
∵四边形ABCD是正方形,
∴BC=DC,∠BCE=90°,
∴∠DCF=180°-∠BCE=180°-90°=90°,
∴∠BCE=∠DCF.
又∵CE=CF,∴△BCE≌△DCF,
∴BE=DF,∠CBF=∠CDF.
∵∠DCF=90°,∴∠CDF+∠F=90°,
∴∠CBE+∠F=90°,
∴∠BMF=90°,∴BE⊥DF.
【互动总结】(学生总结,老师点评)本题是通过证明△BCE≌△DCF来得到BE与DF之间的关系,证明三角形全等是解决这一类型问题的常用做法.
活动2 巩固练习(学生独学)
1.正方形面积为36,则对角线的长为( B )
A.6 B.6
C.9 D.9
2.如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为( C )
A.14 B.15
C.16 D.17
3.如图,延长正方形ABCD的边BC至点E,使CE=AC,连结AE交CD于点F,则∠AFC=112.5°.
活动3 拓展延伸(学生对学)
【例2】如图,正方形ABCD和正方形CGEF的边长分别是3和5,且点B、C、G在同一直线上,M是线段AE的中点,连结MF,求MF的长.
【互动探索】结合已知条件,需作出辅助线,即连结DM并延长交EF于点N,再得到哪两个三角形全等,就可以解决问题?
【解答】连结DM并延长交EF于点N,如图.
∵四边形ABCD,四边形EFCG都是正方形,
∴AD∥BG,EF∥BG,∴EF∥AD,
∴∠NEM=∠DAM.
在△ADM和△ENM中,
∴△ADM≌△ENM,
∴AD=NE=3,DM=MN.
∵EF=5,∴FN=2.
∵DF=FC-CD=2,∴FN=FD,
∴FM是等腰直角△DFN的底边上的中线,所以FM=DN=.
【互动总结】(学生总结,老师点评)正确作出辅助线,结合正方形的性质,构造出全等三角形是解决本题的关键.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
正方形的性质
第2课时 正方形的判定
一、基本目标
1.掌握正方形的判定方法,会运用平行四边形、矩形、菱形、正方形的判定条件进行有关的论证和计算.
2.经历探究正方形判定条件的过程,发展学生初步的综合推理能力,主动探究的学习习惯,逐步掌握说理的基本方法.
二、重难点目标
【教学重点】
掌握正方形的判定条件.
【教学难点】
合理恰当地利用特殊平行四边形的判定进行有关的论证和计算.
三、教学过程
环节1 自学提纲、生成问题
【5 min阅读】
阅读教材P22~P24的内容,完成下面练习.
【3 min反馈】
1.正方形的判定:对角线相等的菱形是正方形;对角线垂直的矩形是正方形;有一个角是直角的菱形是正方形.
2.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是( C )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
环节2 合作探究,解决问题
活动1 小组讨论(师生互学)
【例1】如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
【互动探索】(引发学生思考)由BF∥CE,CF∥BE,可直接得出四边形BECF是哪种特殊四边形?再结合矩形ABCD的性质,又能得出四边形BECF是哪种特殊四边形?
【证明】∵BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴∠ABC=90°,∠DCB=90°.
又∵BE平分∠ABC,CE平分∠DCB,
∴∠EBC=∠ABC=45°,
∠ECB=∠DCB=45°,
∴∠EBC=∠ECB,
∴EB=EC,∴平行四边形BECF是菱形.
在△EBC中,∵∠EBC=45°,∠ECB=45°,
∴∠BEC=90°,∴菱形BECF是正方形.
【互动总结】(学生总结,老师点评)掌握平行四边形、矩形、菱形成为正方形所需要的条件是解决这类问题的关键.
活动2 巩固练习(学生独学)
1.如图,在△ABC中,∠ABC=90°,BD平分∠ABC,DE⊥BC,DF⊥AB,垂足分别为E、F,求证:四边形BEDF是正方形.
证明:∵∠ABC=90°,DE⊥BC,DF⊥AB,∴四边形BEDF是矩形.∵BD平分∠ABC,DE⊥BC,DF⊥AB,∴DE=DF,∴四边形BEDF是正方形.
2.如图,点E、F、G、H分别是CD、BC、AB、DA的中点,求证:四边形EFGH是平行四边形.
证明:连结BD.∵点E、F、G、H分别是CD、BC、AB、DA的中点,∴EF是△BCD的中位线,GH是△ABD的中位线.∴EF∥BD,EF=BD,GH∥BD,GH=BD.∴EF∥GH,且EF=GH.∴四边形EFGH是平行四边形.
活动3 拓展延伸 (学生对学)
【例2】如图,已知E是正方形ABCD的对角线BD上的点,连结AE、CE.
(1)求证:AE=CE;
(2)若将△ABE沿AB翻折后得到△ABF,当点E在BD的何处时,四边形AFBE是正方形?请证明你的结论.
【互动探索】(1)结合已知条件和图形,要证AE=CE,只需证明哪两个三角形全等?(2)由折叠的性质得出哪些结论?
【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=CB,∠BAD=∠ABC=90°,∠ABE=∠CBE=45°,
在△ABE和△CBE中,
∴△ABE≌△CBE(SAS),
∴AE=CE.
(2)点E在BD的中点时,四边形AFBE是正方形.理由:
由折叠的性质,得∠F=∠AEB,AF=AE,BF=BE.
∵∠BAD=90°,AB=AD,E是BD的中点,
∴AE=BD=BE,∠AEB=90°,
∴AE=BE=AF=BF,
∴四边形AFBE是菱形.
又∵∠AEB=90°,
∴四边形AFBE是正方形.
【互动总结】(学生总结,老师点评)图形翻折前后,对应边相等,对应角相等,结合特殊平行四边形的性质与判定、全等三角形的性质求解此类题型.
环节3 课堂小结,当堂达标
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
