2.2.1 直线方程的概念与直线的斜率 课件(19张PPT)
文档属性
| 名称 | 2.2.1 直线方程的概念与直线的斜率 课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 917.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-29 00:00:00 | ||
图片预览


文档简介
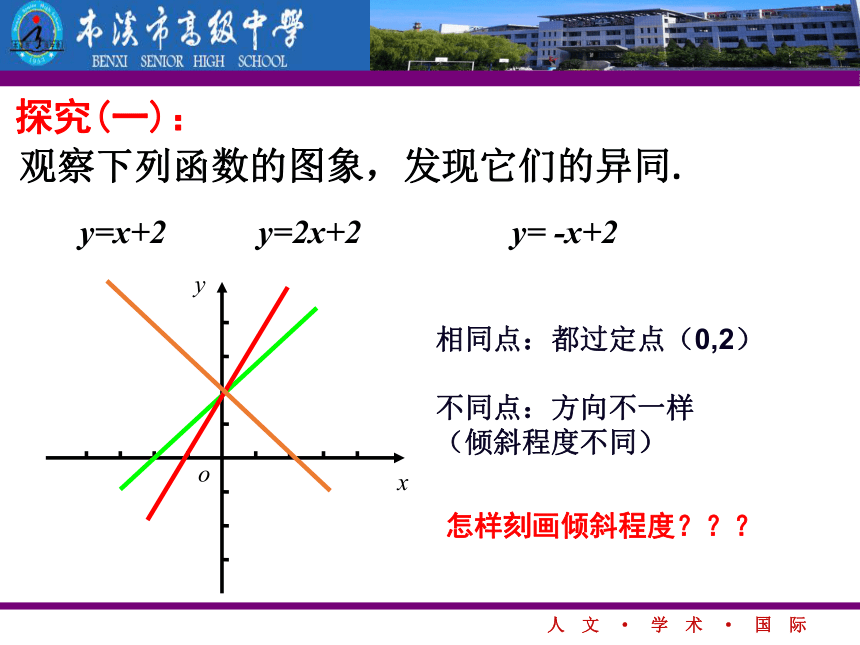
课件19张PPT。2.2.1直线的斜率观察下列函数的图象,发现它们的异同.y=x+2 y=2x+2 y= -x+2相同点:都过定点(0,2)
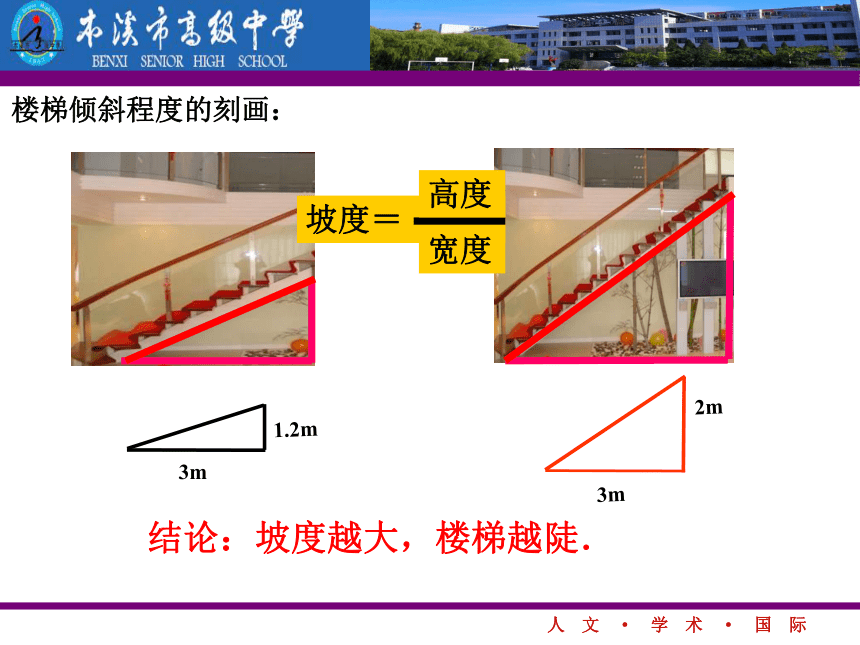
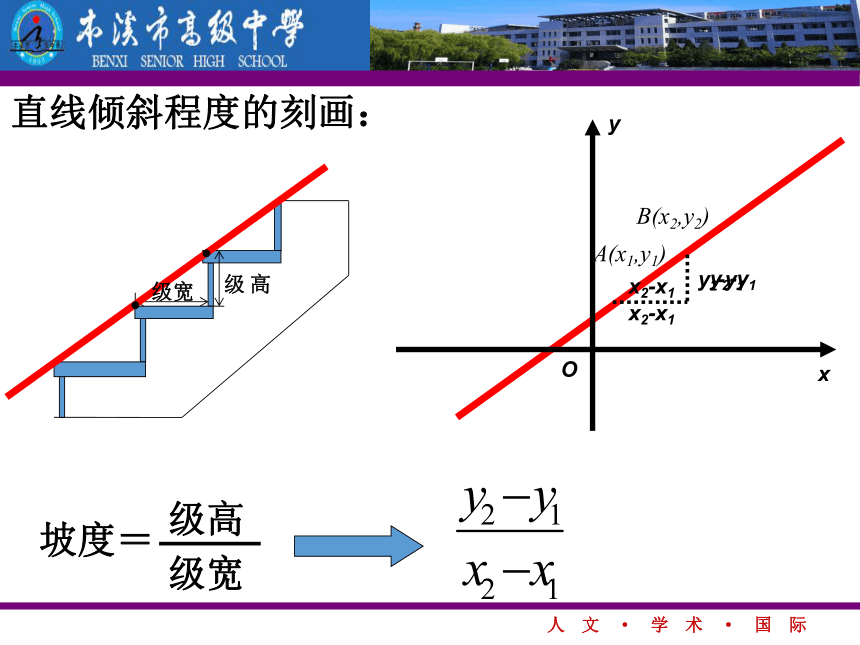
不同点:方向不一样 (倾斜程度不同)探究(一):怎样刻画倾斜程度???结论:坡度越大,楼梯越陡.坡度=高度宽度楼梯倾斜程度的刻画:xyOA(x1,y1)B(x2,y2)级宽高级y2-y1x2-x1x2-x1y2-y1直线倾斜程度的刻画: 是一个定值 对于一条与x轴不垂直的定直线,
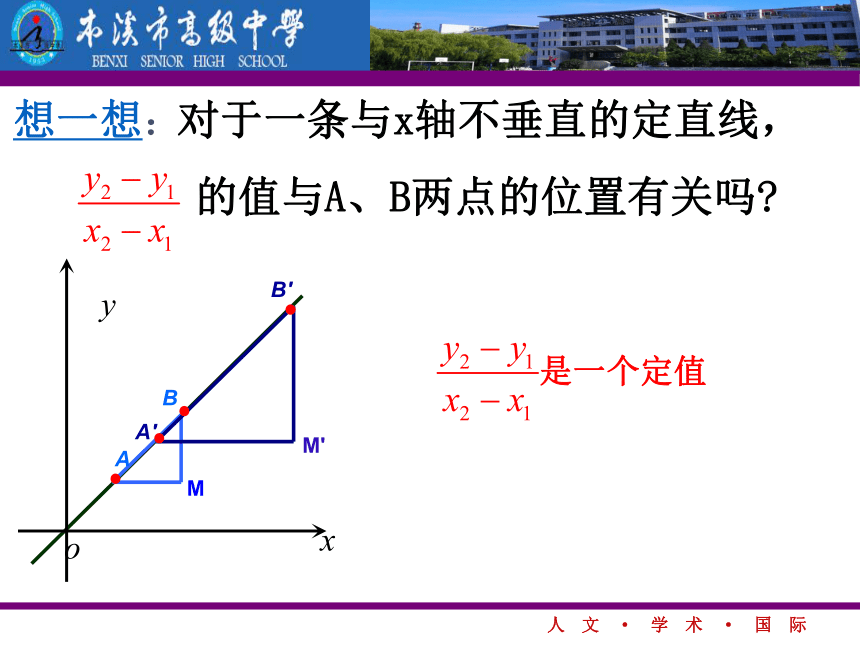
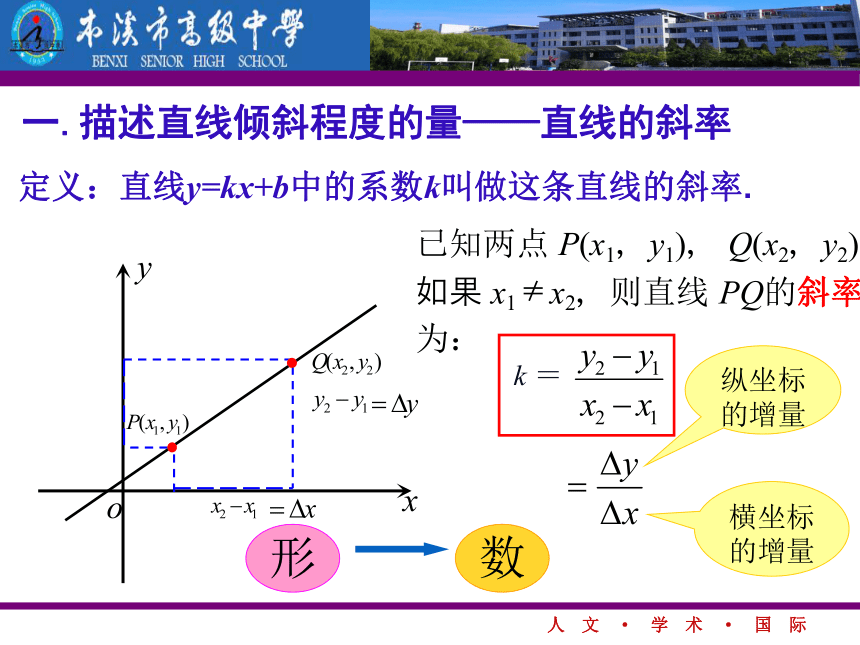
的值与A、B两点的位置有关吗?ABA'B'MM'想一想:等价问题:纵坐标的增量已知两点 P(x1,y1), Q(x2,y2),
如果 x1≠x2,则直线 PQ的斜率
为:
横坐标的增量形数一.描述直线倾斜程度的量——直线的斜率定义:直线y=kx+b中的系数k叫做这条直线的斜率.思考1: 如果 x1=x2,则直线 PQ的斜率怎样?
斜率不存在,这时直线PQ垂直于x轴如果 y1=y2,则直线 PQ的斜率怎样?
斜率为0,这时直线PQ平行于x轴二.直线的倾斜角 x轴正向与直线向上的方向所成的角叫做这条直线的倾斜角.注意: (1)直线向上方向;
(2)x轴的正方向.下列图中标出的直线的倾斜角对不对?如果不对,违背了定义中的哪一条?大家来找茬:观察下列直线的倾斜角,回答下列问题探究(二):问题1.当直线与x轴平行或重合时,直线的倾斜角是多少 ? 问题2.直线倾斜角的范围是怎样的? *规定:与x轴平行或重合的直线的倾斜角为零度角.*倾斜角的取值范围探究(二):问题3.直线的斜率k与直线的倾斜角α之间的关系是怎样的? 当α=00 时,k = 0当00<α<900时,倾斜角α增大,k值也随着增大 当α=900 时,k不存在当900<α<1800时,倾斜角α增大,k值也随着增大 k>0 k<0 求直线斜率的步骤(1)已知直线上两点的坐标;(2)计算两个坐标差△x= ,△y= ;(3)判断⊿x;(4)计算k值.例1.求经过A(-2,0),B(-5,3) 两点的直线的斜率k.解:练一练:
1.经过下列两点的直线的斜率是否存在?
如果存在,求其斜率:(1)(1,-1),(-3,2);
(2)(1,-2),(5,-2);
(3)(3,4),(-2,-5);
(4)(3,0),(3 , ). 2.如图,直线 的斜率分别为 ,则:( )D3.已知过点P(1-a,1+a)和Q(3,2a)的直线的倾斜角为钝角,则实数a的取值范围是 .(-2,1) 4.求过点M(0,2)和N(2,3 +12m+13)(m∈R)的直线l的斜率k的取值范围.解:由斜率公式得直线l 的斜率例2.已知两点A ,B(3,2),过点P(1,0)的直线l与线段AB有公共点.求直线l的斜率k的取值范围.PAB解:如图所示,由题意可知要使直线l与线段AB有公共点,则直线l的斜率k的取值范围是1≤k≤思考题:已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点.
求直线l的斜率k的取值范围.l1PAB斜率不存在k≤-1或k≥1
不同点:方向不一样 (倾斜程度不同)探究(一):怎样刻画倾斜程度???结论:坡度越大,楼梯越陡.坡度=高度宽度楼梯倾斜程度的刻画:xyOA(x1,y1)B(x2,y2)级宽高级y2-y1x2-x1x2-x1y2-y1直线倾斜程度的刻画: 是一个定值 对于一条与x轴不垂直的定直线,
的值与A、B两点的位置有关吗?ABA'B'MM'想一想:等价问题:纵坐标的增量已知两点 P(x1,y1), Q(x2,y2),
如果 x1≠x2,则直线 PQ的斜率
为:
横坐标的增量形数一.描述直线倾斜程度的量——直线的斜率定义:直线y=kx+b中的系数k叫做这条直线的斜率.思考1: 如果 x1=x2,则直线 PQ的斜率怎样?
斜率不存在,这时直线PQ垂直于x轴如果 y1=y2,则直线 PQ的斜率怎样?
斜率为0,这时直线PQ平行于x轴二.直线的倾斜角 x轴正向与直线向上的方向所成的角叫做这条直线的倾斜角.注意: (1)直线向上方向;
(2)x轴的正方向.下列图中标出的直线的倾斜角对不对?如果不对,违背了定义中的哪一条?大家来找茬:观察下列直线的倾斜角,回答下列问题探究(二):问题1.当直线与x轴平行或重合时,直线的倾斜角是多少 ? 问题2.直线倾斜角的范围是怎样的? *规定:与x轴平行或重合的直线的倾斜角为零度角.*倾斜角的取值范围探究(二):问题3.直线的斜率k与直线的倾斜角α之间的关系是怎样的? 当α=00 时,k = 0当00<α<900时,倾斜角α增大,k值也随着增大 当α=900 时,k不存在当900<α<1800时,倾斜角α增大,k值也随着增大 k>0 k<0 求直线斜率的步骤(1)已知直线上两点的坐标;(2)计算两个坐标差△x= ,△y= ;(3)判断⊿x;(4)计算k值.例1.求经过A(-2,0),B(-5,3) 两点的直线的斜率k.解:练一练:
1.经过下列两点的直线的斜率是否存在?
如果存在,求其斜率:(1)(1,-1),(-3,2);
(2)(1,-2),(5,-2);
(3)(3,4),(-2,-5);
(4)(3,0),(3 , ). 2.如图,直线 的斜率分别为 ,则:( )D3.已知过点P(1-a,1+a)和Q(3,2a)的直线的倾斜角为钝角,则实数a的取值范围是 .(-2,1) 4.求过点M(0,2)和N(2,3 +12m+13)(m∈R)的直线l的斜率k的取值范围.解:由斜率公式得直线l 的斜率例2.已知两点A ,B(3,2),过点P(1,0)的直线l与线段AB有公共点.求直线l的斜率k的取值范围.PAB解:如图所示,由题意可知要使直线l与线段AB有公共点,则直线l的斜率k的取值范围是1≤k≤思考题:已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点.
求直线l的斜率k的取值范围.l1PAB斜率不存在k≤-1或k≥1
