2.2.3 两条直线的位置关系(一) 课件(23张PPT)
文档属性
| 名称 | 2.2.3 两条直线的位置关系(一) 课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-29 00:00:00 | ||
图片预览








文档简介
课件23张PPT。两条直线的位置关系--第一课时一、复习提问:你知道用什么来刻画直线的倾斜程度吗?回忆直线方程的一般式和斜截式。 平面内两条直线的位置关系有哪几种? 两条直线的倾斜角相等,这两条直线的位置关系如何?提问:平行相交重合探究问题:在同一平面直角坐标系下,分别作出下列两组方程的直线,从图中你发现了什么规律并说明理由。
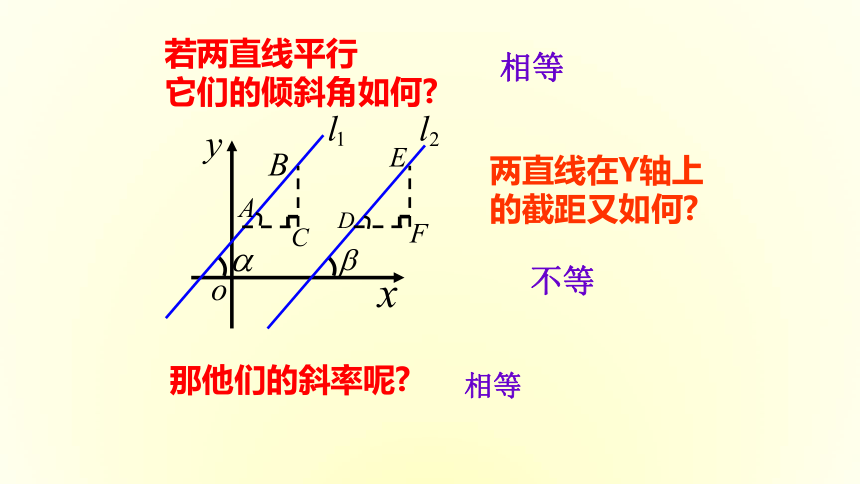
(1)(2)若两直线平行
它们的倾斜角如何?那他们的斜率呢?相等相等两直线在Y轴上的截距又如何?不等 当两条直线斜率存在时
l1:y = k1 x +b 1 l2: y = k2 x +b 2 时 直线 l1 ∥l2 的条件是什么? 若两直线l1 、l2斜率都不存在也不重合则两直线位置关系怎样?k1 = k2 且 b 1 ≠b 2 .l1:x=a1 l2: x=a2( a1 ≠ a2 ) l1 ∥l2 判断两条直线位置关系的程序两条直线方程化为斜截式方程两条直线斜率截距两条直线斜率都不存在 平行或重合k1= k2 b1≠b2平行相交k1= k2 b1= b2重合k1 ≠ k2 若两直线方程均为一般式时,我们又如何判定两直线平行,相交,重合呢?从代数方法的角度入手一、两条直线相交和平行与重合条件 1、l1:A1x+B1 y+C1=0与 l2:A2x+B2 y+C2=0。将直线方程联立,得(1)(2)若方程组有唯一解,则两直线相交,交点坐标
就是方程组的解;
若方程组无解,则两直线平行;
若方程组有无穷多个解,则两直线重合。相交平行重合总结l1∥l2 的条件?l1:A1x + B1y +C1 = 0,
l2:A2x + B2y +C2 = 0
(A1与B1不全为零、A2与B2也不全为零)重要结论l1∥l2 ?
A1 B2 – A2 B1= 0且A1 C2 – A2 C1 0
或l1:A1x + B1y +C1 = 0,
l2:A2x + B2y +C2 = 0
(A1与B1不全为零、A2与B2也不全为零)例1.判断下列各组直线的位置关系
(2)(3)(4)(1)例2: 分别求这组直线平行,重合,相交时实数a的值。变式练习分别求这组直线平行,重合,相交时 的值分析:求直线的方程需要哪些条件?还差什么条件?可以怎么求?例3: 求过点A(1,-4),且与直线2x+3y+5=0平行的直线方程. 例3.求过点 A(1,- 4)且与直线 2x+3y+5 = 0 平行的直线的方程. 解法1:已知直线的斜率是– 2/3 ,
又所求直线与已知直线平行,
所以它的斜率也是– 2/3. 所以设所求直线方程是y = - 2/3x+b,代入x=1,y=-4, 即 2x+3y+10 = 0 .重要方法例3: 求过点A(1,-4),且与直线2x+3y+5=0平行的直线方程. 你的结果2x+3y+10=0与已知直线2x+3y+5=0有什么不同?法2:设所求直线为2x+3y+c=0
将x=1,y=-4代入得2x+3y+10=0变式练习:作业题四、课堂小结:两直线平行,重合,相交的条件是什么?
1、
两直线平行,重合的充要条件是什么?
2、
或作业教材84页:练习A,
练习B
(1)(2)若两直线平行
它们的倾斜角如何?那他们的斜率呢?相等相等两直线在Y轴上的截距又如何?不等 当两条直线斜率存在时
l1:y = k1 x +b 1 l2: y = k2 x +b 2 时 直线 l1 ∥l2 的条件是什么? 若两直线l1 、l2斜率都不存在也不重合则两直线位置关系怎样?k1 = k2 且 b 1 ≠b 2 .l1:x=a1 l2: x=a2( a1 ≠ a2 ) l1 ∥l2 判断两条直线位置关系的程序两条直线方程化为斜截式方程两条直线斜率截距两条直线斜率都不存在 平行或重合k1= k2 b1≠b2平行相交k1= k2 b1= b2重合k1 ≠ k2 若两直线方程均为一般式时,我们又如何判定两直线平行,相交,重合呢?从代数方法的角度入手一、两条直线相交和平行与重合条件 1、l1:A1x+B1 y+C1=0与 l2:A2x+B2 y+C2=0。将直线方程联立,得(1)(2)若方程组有唯一解,则两直线相交,交点坐标
就是方程组的解;
若方程组无解,则两直线平行;
若方程组有无穷多个解,则两直线重合。相交平行重合总结l1∥l2 的条件?l1:A1x + B1y +C1 = 0,
l2:A2x + B2y +C2 = 0
(A1与B1不全为零、A2与B2也不全为零)重要结论l1∥l2 ?
A1 B2 – A2 B1= 0且A1 C2 – A2 C1 0
或l1:A1x + B1y +C1 = 0,
l2:A2x + B2y +C2 = 0
(A1与B1不全为零、A2与B2也不全为零)例1.判断下列各组直线的位置关系
(2)(3)(4)(1)例2: 分别求这组直线平行,重合,相交时实数a的值。变式练习分别求这组直线平行,重合,相交时 的值分析:求直线的方程需要哪些条件?还差什么条件?可以怎么求?例3: 求过点A(1,-4),且与直线2x+3y+5=0平行的直线方程. 例3.求过点 A(1,- 4)且与直线 2x+3y+5 = 0 平行的直线的方程. 解法1:已知直线的斜率是– 2/3 ,
又所求直线与已知直线平行,
所以它的斜率也是– 2/3. 所以设所求直线方程是y = - 2/3x+b,代入x=1,y=-4, 即 2x+3y+10 = 0 .重要方法例3: 求过点A(1,-4),且与直线2x+3y+5=0平行的直线方程. 你的结果2x+3y+10=0与已知直线2x+3y+5=0有什么不同?法2:设所求直线为2x+3y+c=0
将x=1,y=-4代入得2x+3y+10=0变式练习:作业题四、课堂小结:两直线平行,重合,相交的条件是什么?
1、
两直线平行,重合的充要条件是什么?
2、
或作业教材84页:练习A,
练习B
