2.3.1 圆的标准方程 课件(21张PPT)
文档属性
| 名称 | 2.3.1 圆的标准方程 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 267.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-29 09:27:28 | ||
图片预览





文档简介
课件21张PPT。圆的标准方程问题提出1.在平面直角坐标系中,两点确定一条
直线,一点和倾斜角也确定一条直线,
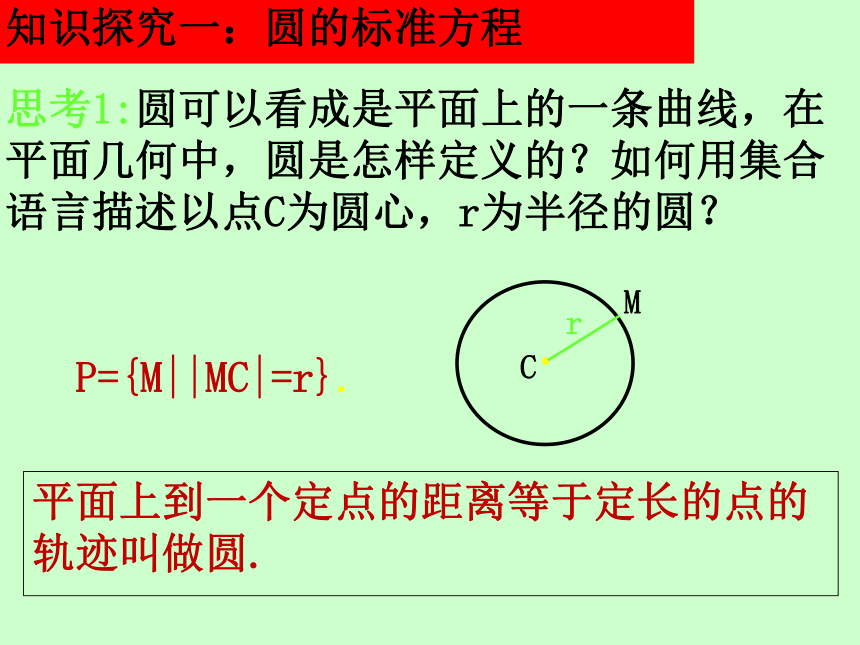
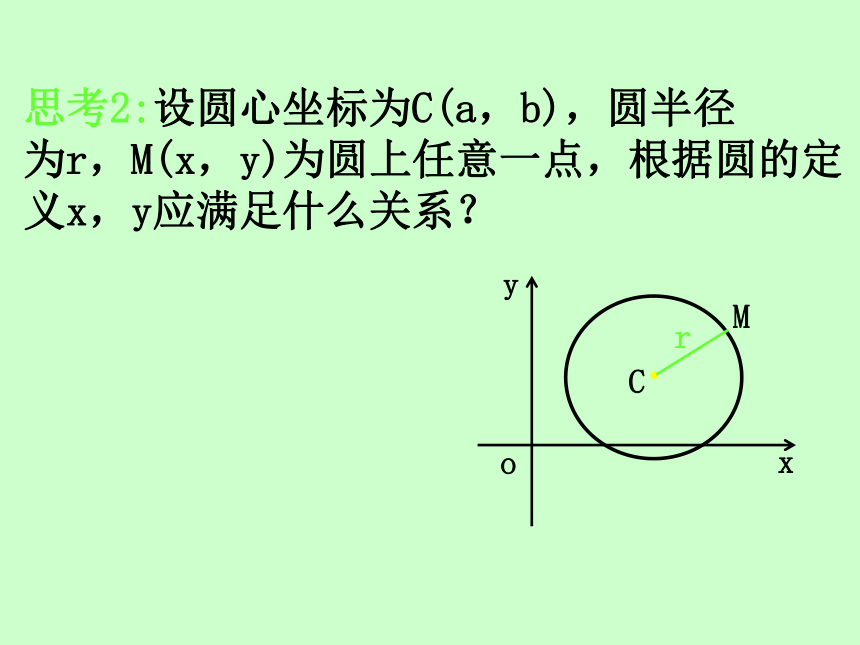
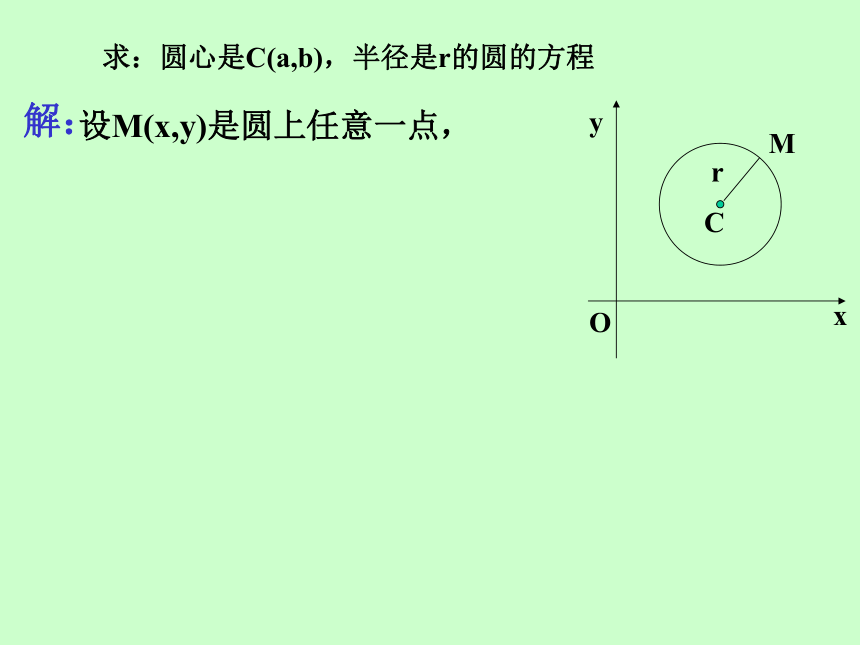
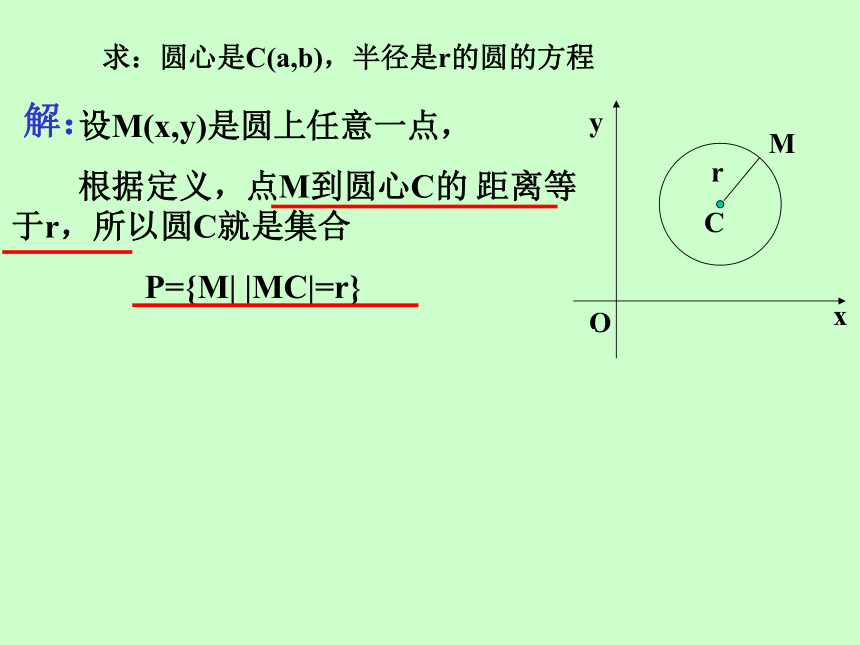
那么在什么条件下可以确定一个圆呢?2.直线可以用一个方程表示,圆也可以用一个方程来表示,怎样建立圆的方程是我们需要探究的问题. 圆心和半径知识探究一:圆的标准方程 平面上到一个定点的距离等于定长的点的轨迹叫做圆. P={M||MC|=r}.思考2:设圆心坐标为C(a,b),圆半径
为r,M(x,y)为圆上任意一点,根据圆的定义x,y应满足什么关系?解:解:解:解:特例:如果圆心在坐标原点,圆的方程为 x2+y2=r2.【做一做】 圆x2+y2=1的圆心坐标为( )
A.(0,0) B.(1,1) C.(0,1) D.(1,0)
【做一做】 圆(x-1)2+(y+2)2=2的半
径为( )
A.1 B. C.2 D.4C 类AB类C类AB类例1.写出圆心为A(2,-3)半径长等于5的圆 的方程,
并判断点M1(5,-7),M2(- ,-1)
是否在这个圆上。思考1:在平面几何中,点与圆有哪几种位置关系? OArOA=r练习
1.已知圆C:(x-5)2+(y-6)2=10,试判断点M(6,9), N(3,3),Q(5,3)与圆C的位置关系.(C类)
2.已知点A(1,2)在圆C:(x-a)2+(y+a)2=2a2的内部,求实数a的取值范围. (B类)
3.已知圆C:(x-1)2+(y+2)2=4,点P(x0,y0)在圆C的内部,且d=(x0-1)2+(y0+2)2,则有( ) (A类)
A.d>2 B.0≤d<2 C.d>4 D.0≤d<4
2.已知点A(1,2)在圆C:(x-a)2+(y+a)2=2a2的内部,求实数a的取值范围.
解:因为点A在圆的内部,
所以(1-a)2+(2+a)2<2a2,
所以2a+5<0,3.已知圆C:(x-1)2+(y+2)2=4,点P(x0,y0)在圆C的内部,
且d=(x0-1)2+(y0+2)2,则有( )
A.d>2 B.0≤d<2 C.d>4 D.0≤d<4
答案:D例2:
三角形ABC的三个顶点的坐标分别是
求它的外接圆的方程.作为练习: 请完成课本121页练习第4题补充练习
1.圆心为(0,4),且过点(3,0)的圆的方程为( ) (C类)
A.x2+(y-4)2=25 B.x2+(y+4)2=25
C.(x-4)2+y2=25 D.(x+4)2+y2=25
2.已知圆的方程是(x-2)2+(y-3)2=4,
则点 P(3,2) ( C类 )
A.是圆心 B.在圆上 C.在圆内 D.在圆外
3.点P(1,-1)在圆(x+2)2+y2=m的外部,
则实数m的取值范围是__________. ( AB类)
4.已知△ABC的三个顶点分别为A(1,1),B(1,4),
C(5,1),求它的外接圆的方程.(3)点与圆的位置关系
直线,一点和倾斜角也确定一条直线,
那么在什么条件下可以确定一个圆呢?2.直线可以用一个方程表示,圆也可以用一个方程来表示,怎样建立圆的方程是我们需要探究的问题. 圆心和半径知识探究一:圆的标准方程 平面上到一个定点的距离等于定长的点的轨迹叫做圆. P={M||MC|=r}.思考2:设圆心坐标为C(a,b),圆半径
为r,M(x,y)为圆上任意一点,根据圆的定义x,y应满足什么关系?解:解:解:解:特例:如果圆心在坐标原点,圆的方程为 x2+y2=r2.【做一做】 圆x2+y2=1的圆心坐标为( )
A.(0,0) B.(1,1) C.(0,1) D.(1,0)
【做一做】 圆(x-1)2+(y+2)2=2的半
径为( )
A.1 B. C.2 D.4C 类AB类C类AB类例1.写出圆心为A(2,-3)半径长等于5的圆 的方程,
并判断点M1(5,-7),M2(- ,-1)
是否在这个圆上。思考1:在平面几何中,点与圆有哪几种位置关系? OA
1.已知圆C:(x-5)2+(y-6)2=10,试判断点M(6,9), N(3,3),Q(5,3)与圆C的位置关系.(C类)
2.已知点A(1,2)在圆C:(x-a)2+(y+a)2=2a2的内部,求实数a的取值范围. (B类)
3.已知圆C:(x-1)2+(y+2)2=4,点P(x0,y0)在圆C的内部,且d=(x0-1)2+(y0+2)2,则有( ) (A类)
A.d>2 B.0≤d<2 C.d>4 D.0≤d<4
2.已知点A(1,2)在圆C:(x-a)2+(y+a)2=2a2的内部,求实数a的取值范围.
解:因为点A在圆的内部,
所以(1-a)2+(2+a)2<2a2,
所以2a+5<0,3.已知圆C:(x-1)2+(y+2)2=4,点P(x0,y0)在圆C的内部,
且d=(x0-1)2+(y0+2)2,则有( )
A.d>2 B.0≤d<2 C.d>4 D.0≤d<4
答案:D例2:
三角形ABC的三个顶点的坐标分别是
求它的外接圆的方程.作为练习: 请完成课本121页练习第4题补充练习
1.圆心为(0,4),且过点(3,0)的圆的方程为( ) (C类)
A.x2+(y-4)2=25 B.x2+(y+4)2=25
C.(x-4)2+y2=25 D.(x+4)2+y2=25
2.已知圆的方程是(x-2)2+(y-3)2=4,
则点 P(3,2) ( C类 )
A.是圆心 B.在圆上 C.在圆内 D.在圆外
3.点P(1,-1)在圆(x+2)2+y2=m的外部,
则实数m的取值范围是__________. ( AB类)
4.已知△ABC的三个顶点分别为A(1,1),B(1,4),
C(5,1),求它的外接圆的方程.(3)点与圆的位置关系
