2.3.1 圆的标准方程 课件(22张PPT)
文档属性
| 名称 | 2.3.1 圆的标准方程 课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 728.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-29 00:00:00 | ||
图片预览







文档简介
课件22张PPT。蜻蜓点水泛涟漪太极之道阴阳生小憩片刻顿生情车水马龙霓虹灯生活剪影圆的历史 约在6000年前,美索不达米亚人,做出了世界上第一个轮子——圆型的木盘。 古代埃及人就认为:圆,是神赐给人的神圣图形。
... 直到2000多年前,我国的墨子(约公元前468-前376年)才给圆下了一个定义:圆,一中同长也。数学的美丽邂逅 在微信刚盛行的时候,大家喜欢“摇一摇”,男孩和女孩就这样认识了,一聊就是三年,男孩爱上了女孩,男未婚女未嫁,羞涩的男孩终于提出了约会。 腼腆的女孩面对网络中的心仪男孩,提出了一个考验:如果你能在一周内找到我家的位置,我就嫁给你! 约定:一周内不少于三次待在家里时,开启附近的人功能;男孩记录了三个位置,并且每次与女孩的家距离都相等;男孩将高德地图打印出来,建立平面直角坐标系,得到记录三个点的坐标是 ,(0,0),(0,3)。女孩的家在哪里?4.1圆的标准方程1、什么是圆?定义:平面内到定点距离等于定长的点的轨迹是圆.2、确定圆需要几个要素?圆心--确定圆的位置
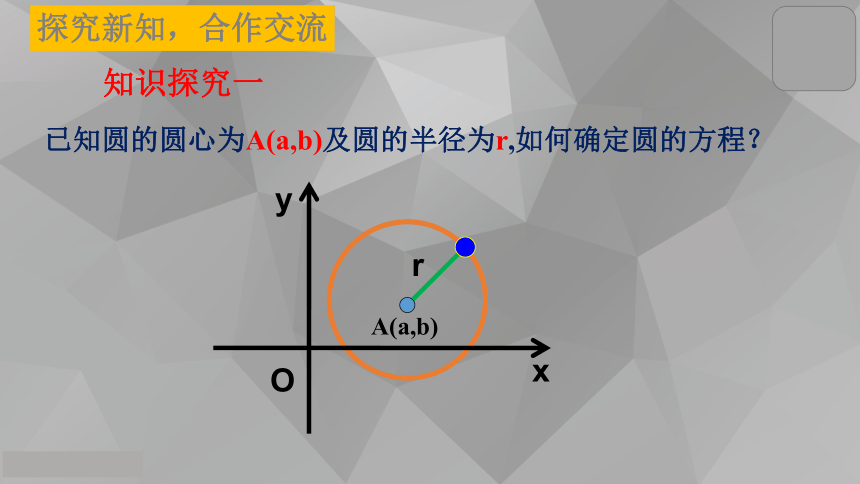
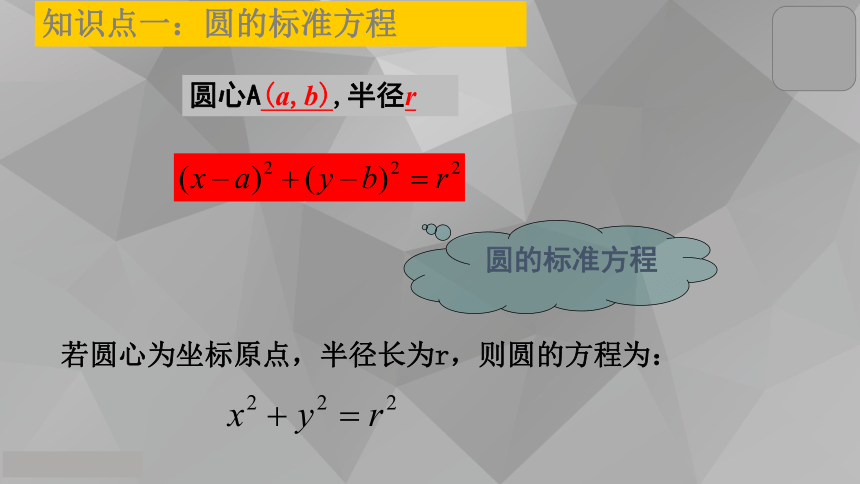
半径--确定圆的大小自主学习,合作解疑知识探究一 已知圆的圆心为A(a,b)及圆的半径为r,如何确定圆的方程?A(a,b)r探究新知,合作交流xy则|MA|= r { M | |MA| = r }圆上所有点的集合 如图,在直角坐标系中,圆心A的位置用坐标 (a,b) 表示,半径 r的大小等于圆上任意点M(x, y)与圆心A (a,b) 的距离.(1)知识探究一:圆的标准方程圆心A(a,b),半径r若圆心为坐标原点,半径长为r,则圆的方程为:圆的标准方程
知识点一:圆的标准方程小试牛刀1.圆 (x-2)2+ y2=2的圆心A的坐标为______,半径r=__. 2.圆心坐标是(-1,2),点A(1,1)在圆上,圆的方程是_______________.(2,0)(x+1)2+(x-2)2=5 已知圆x2+y2=5,判断点A(1,2)关于圆心对称的点A1是否在圆上,关于y轴对称的点A2呢?思考解:圆心坐标(0,0),A1(-1,-2),A1坐标满足圆的方程,所以A1在圆上; 圆心坐标(0,0),y轴经过圆心,∴y轴是圆的一条对称轴,A2(-1,2),A2坐标满足圆的方程,所以A2在圆上。 例1.写出圆心为A(2,-3),半径长等于5的圆的方程,并判断点M1(5,-7) , 是否在这个圆上。 解:圆心是A(2,-3) ,半径长等于5的圆的标准方程是: 把M1(5,-7)的坐标代入方程 左右两边相等,点M1的坐标适合圆的方程,所以点M1在这个圆上; 把点 的坐标代入此方程,左右两边不相等,点M2的坐标不适合圆的方程,所以点M2不在这个圆上.典例分析怎样判断点 在圆上?圆内?还是在圆外呢?CxyoM3知识探究二探究新知,合作交流知识探究二:点与圆的位置关系 探究:在平面几何中,如何确定点与圆的位置关系?MO|OM|r点在圆内点在圆上点在圆外(x0-a)2+(y0-b)2r2时,点M在圆C外.点与圆的位置关系:知识点二:点与圆的位置关系小试牛刀3.点P(1,5)与圆x2+y2=25的位置关系( )
A在圆外 B在圆上 C在圆内 D在圆上或圆外A 例2 △AOB三个顶点坐标分别为A , 0(0,0),B(0,3),求它的外接圆方程,并写出其圆心坐标. 解:设所求圆的方程是 (1)因为A(4,0), 0(0,0),B(0,3)都在圆上,所以它们的坐标都满足方程(1).于是待定系数法所求圆的方程为∴圆心坐标为 半径为典例分析圆经过A(1,1),B(2,-2)解1:设圆C的方程为∵圆心在直线l:x-y+1=0上待定系数法 变式 己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.典例分析弦AB的垂直平分线圆心:两条直线的交点半径:圆心到圆上一点xyOA(1,1)B(2,-2)D 变式 己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.典例分析解:∵A(1,1),B(2,-2)即:x-3y-3=0∴圆心C(-3,-2) 变式 己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.典例分析课堂小结:通过本节课的学习,你主要收获有哪些?关键词:三种语言,求解方程,数学思想,情感体验,等。作业布置P120 练习1
P121 练习3、4 P124 习题A组3谢谢聆听
... 直到2000多年前,我国的墨子(约公元前468-前376年)才给圆下了一个定义:圆,一中同长也。数学的美丽邂逅 在微信刚盛行的时候,大家喜欢“摇一摇”,男孩和女孩就这样认识了,一聊就是三年,男孩爱上了女孩,男未婚女未嫁,羞涩的男孩终于提出了约会。 腼腆的女孩面对网络中的心仪男孩,提出了一个考验:如果你能在一周内找到我家的位置,我就嫁给你! 约定:一周内不少于三次待在家里时,开启附近的人功能;男孩记录了三个位置,并且每次与女孩的家距离都相等;男孩将高德地图打印出来,建立平面直角坐标系,得到记录三个点的坐标是 ,(0,0),(0,3)。女孩的家在哪里?4.1圆的标准方程1、什么是圆?定义:平面内到定点距离等于定长的点的轨迹是圆.2、确定圆需要几个要素?圆心--确定圆的位置
半径--确定圆的大小自主学习,合作解疑知识探究一 已知圆的圆心为A(a,b)及圆的半径为r,如何确定圆的方程?A(a,b)r探究新知,合作交流xy则|MA|= r { M | |MA| = r }圆上所有点的集合 如图,在直角坐标系中,圆心A的位置用坐标 (a,b) 表示,半径 r的大小等于圆上任意点M(x, y)与圆心A (a,b) 的距离.(1)知识探究一:圆的标准方程圆心A(a,b),半径r若圆心为坐标原点,半径长为r,则圆的方程为:圆的标准方程
知识点一:圆的标准方程小试牛刀1.圆 (x-2)2+ y2=2的圆心A的坐标为______,半径r=__. 2.圆心坐标是(-1,2),点A(1,1)在圆上,圆的方程是_______________.(2,0)(x+1)2+(x-2)2=5 已知圆x2+y2=5,判断点A(1,2)关于圆心对称的点A1是否在圆上,关于y轴对称的点A2呢?思考解:圆心坐标(0,0),A1(-1,-2),A1坐标满足圆的方程,所以A1在圆上; 圆心坐标(0,0),y轴经过圆心,∴y轴是圆的一条对称轴,A2(-1,2),A2坐标满足圆的方程,所以A2在圆上。 例1.写出圆心为A(2,-3),半径长等于5的圆的方程,并判断点M1(5,-7) , 是否在这个圆上。 解:圆心是A(2,-3) ,半径长等于5的圆的标准方程是: 把M1(5,-7)的坐标代入方程 左右两边相等,点M1的坐标适合圆的方程,所以点M1在这个圆上; 把点 的坐标代入此方程,左右两边不相等,点M2的坐标不适合圆的方程,所以点M2不在这个圆上.典例分析怎样判断点 在圆上?圆内?还是在圆外呢?CxyoM3知识探究二探究新知,合作交流知识探究二:点与圆的位置关系 探究:在平面几何中,如何确定点与圆的位置关系?MO|OM|
A在圆外 B在圆上 C在圆内 D在圆上或圆外A 例2 △AOB三个顶点坐标分别为A , 0(0,0),B(0,3),求它的外接圆方程,并写出其圆心坐标. 解:设所求圆的方程是 (1)因为A(4,0), 0(0,0),B(0,3)都在圆上,所以它们的坐标都满足方程(1).于是待定系数法所求圆的方程为∴圆心坐标为 半径为典例分析圆经过A(1,1),B(2,-2)解1:设圆C的方程为∵圆心在直线l:x-y+1=0上待定系数法 变式 己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.典例分析弦AB的垂直平分线圆心:两条直线的交点半径:圆心到圆上一点xyOA(1,1)B(2,-2)D 变式 己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.典例分析解:∵A(1,1),B(2,-2)即:x-3y-3=0∴圆心C(-3,-2) 变式 己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.典例分析课堂小结:通过本节课的学习,你主要收获有哪些?关键词:三种语言,求解方程,数学思想,情感体验,等。作业布置P120 练习1
P121 练习3、4 P124 习题A组3谢谢聆听
