2.2.2 用样本的数字特征估计总体的数字特征 课件(17张PPT)
文档属性
| 名称 | 2.2.2 用样本的数字特征估计总体的数字特征 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 112.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-29 00:00:00 | ||
图片预览






文档简介
课件17张PPT。用样本的数字特征估计总体的数字特征探究一: 1.平均数的计算公式:
一般地,n个样本数据 的平均数
为 ___________________。 一般地,设样本的元素为 样本的平均数为 ,定义:
=______________________, =_____
其中, 表示________,n表示 ________,
表示 _________。
2. 方差与标准差的计算公式:样本方差样本容量样本标准差3、方差和标准差的意义
用于考察样本数据的离散程度的大小,
标准差越大,数据的离散程度____;标准差
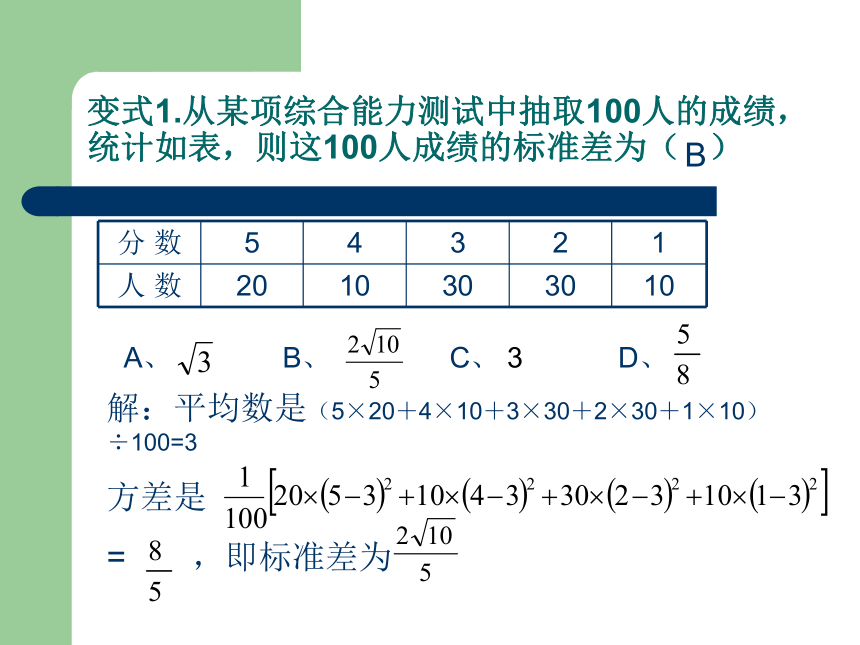
越小,数据的离散程度____。 越大越小例1.计算数据5,7,7,8,11,10的方差和标准差。 变式1.从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为( )A、 B、 C、 3 D、 B解:平均数是(5×20+4×10+3×30+2×30+1×10)÷100=3
方差是
= ,即标准差为思考:平均数越大越好么?方差越小越好么?为什么?举例说明。
例2.从甲?乙两名学生中选拔一人参加射击比赛,对他们的射击水平进行了测试,两人在相同条件下各射击10次,命中的环数如下:甲: 7,8,6,8,6,5,9,10,7,4
乙:9,5,7,8,7,6,8,6,7,7
(1)计算甲、乙两人射击命中环数的平均数与标准差;
(2)比较两人的成绩,然后决定选择哪一人参赛. (1)计算可得
(2) 由(1)可得,甲、乙两人的平均成绩相等,但
,这表明乙的成绩比甲的成绩稳定一些,
从成绩的稳定性考虑,可以选择乙参赛。变式2.从甲、乙两种玉米苗种各抽10株,分别测得它们的株高如下:(单位:厘米)解:
所以乙玉米长得高,甲玉米长得齐问(1)哪种玉米的苗长得高?
(2)哪种玉米的苗长得齐?探究二:观察数据5,7,7,8,10,11。
回答下列问题:
(1)这组数据平均数会不会比5小?
(2)这组数据平均数会不会比11大?
(3)你能否估计一下这组数的平均数是多少?
=8+ [(5-8)+(7-8)+(7-8)+(8-8)+(10-8)+(11-8)]
= 8求下列数据平均数:数据一: 5 , 6 , 6 , 7 , 8 , 8, 9 ,11,12
数据二: 5 , 6 , 6 , 7 , 8, 8, 9,11,13
与8作差:(-3),(-2),(-2),(-1),0 , 0 , 1 , 3 ,4
作和:= 0,所以平均数为8与8作差:(-3),(-2),(-2),(-1),0, 0, 1, 3 , 5
作和:= 0,所以平均数为8求下列数据平均数:数据三: 4 , 5 , 6 , 7 , 8 , 8 , 9 , 11, 12
数据四: 5 , 6 , 6 , 7 , 8 , 8, 9, 11
与8作差: (-4),(-3),(-2),(-1), 0 , 0 , 1, 3, 4
作和: = -2,所以平均数应为8+(-2)÷9
与7作差: (-2),(-1),(-1), 0 , 1 , 1, 2, 4
作和: =4,所以平均数应为7+4÷8小结:(总结新方法的优缺点)缺点:1.多做了一步运算。
2.不能解决所有求平均数问题。
优点:1.把数据变小,使计算更简单,大大的提高了做题的准确率与速度;
2.如果估算准确的情况下,求方差时可直接借用上一步结果;
3.对于有规律的数据可用新方法口算得出结果。求平均数与方差:(1) 7, 8, 6 , 8 , 6 , 5 , 9 ,10,7,4
与7作差:0, 1,(-1),1 ,(-1),(-2), 2, 3 ,0,(-3)
作和 = 0,所以平均数为7
(2) 9 , 5 , 7 , 8 , 7 , 6 , 8 , 6 , 7, 7
与7作差:2 ,(-2), 0 , 1 , 0 ,(-1), 1 ,(-1), 0 , 0
作和= 0,所以平均数为7(3) 14 , 19 , 21 , 22 , 25 ,37,39,40,41,42
与30作差:(-16), (-11),(-9),(-8) ,(-5), 7 , 9,10,11,12
作和 = 0,所以平均数为30
(4) 16 , 16 , 16 , 27, 27,40,40,40,44,44
与30作差:(-14),(-14),(-14),(-3),(-3),10,10,10,14,14
作和 = 10,所以平均数为30 + 10÷10 = 31课堂小结:1.学会了怎样求平均数、方差与标准差。
2.学会了什么叫用样本的数字特征估计总体的数字特征,究竟用样本的数字特征估计总体的数字特征能解决什么实际问题。
3.学会了新的求平均数的方法。
完成课后案
教材 P70,练习 A 1,2
练习 B 1,2
作业:
一般地,n个样本数据 的平均数
为 ___________________。 一般地,设样本的元素为 样本的平均数为 ,定义:
=______________________, =_____
其中, 表示________,n表示 ________,
表示 _________。
2. 方差与标准差的计算公式:样本方差样本容量样本标准差3、方差和标准差的意义
用于考察样本数据的离散程度的大小,
标准差越大,数据的离散程度____;标准差
越小,数据的离散程度____。 越大越小例1.计算数据5,7,7,8,11,10的方差和标准差。 变式1.从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为( )A、 B、 C、 3 D、 B解:平均数是(5×20+4×10+3×30+2×30+1×10)÷100=3
方差是
= ,即标准差为思考:平均数越大越好么?方差越小越好么?为什么?举例说明。
例2.从甲?乙两名学生中选拔一人参加射击比赛,对他们的射击水平进行了测试,两人在相同条件下各射击10次,命中的环数如下:甲: 7,8,6,8,6,5,9,10,7,4
乙:9,5,7,8,7,6,8,6,7,7
(1)计算甲、乙两人射击命中环数的平均数与标准差;
(2)比较两人的成绩,然后决定选择哪一人参赛. (1)计算可得
(2) 由(1)可得,甲、乙两人的平均成绩相等,但
,这表明乙的成绩比甲的成绩稳定一些,
从成绩的稳定性考虑,可以选择乙参赛。变式2.从甲、乙两种玉米苗种各抽10株,分别测得它们的株高如下:(单位:厘米)解:
所以乙玉米长得高,甲玉米长得齐问(1)哪种玉米的苗长得高?
(2)哪种玉米的苗长得齐?探究二:观察数据5,7,7,8,10,11。
回答下列问题:
(1)这组数据平均数会不会比5小?
(2)这组数据平均数会不会比11大?
(3)你能否估计一下这组数的平均数是多少?
=8+ [(5-8)+(7-8)+(7-8)+(8-8)+(10-8)+(11-8)]
= 8求下列数据平均数:数据一: 5 , 6 , 6 , 7 , 8 , 8, 9 ,11,12
数据二: 5 , 6 , 6 , 7 , 8, 8, 9,11,13
与8作差:(-3),(-2),(-2),(-1),0 , 0 , 1 , 3 ,4
作和:= 0,所以平均数为8与8作差:(-3),(-2),(-2),(-1),0, 0, 1, 3 , 5
作和:= 0,所以平均数为8求下列数据平均数:数据三: 4 , 5 , 6 , 7 , 8 , 8 , 9 , 11, 12
数据四: 5 , 6 , 6 , 7 , 8 , 8, 9, 11
与8作差: (-4),(-3),(-2),(-1), 0 , 0 , 1, 3, 4
作和: = -2,所以平均数应为8+(-2)÷9
与7作差: (-2),(-1),(-1), 0 , 1 , 1, 2, 4
作和: =4,所以平均数应为7+4÷8小结:(总结新方法的优缺点)缺点:1.多做了一步运算。
2.不能解决所有求平均数问题。
优点:1.把数据变小,使计算更简单,大大的提高了做题的准确率与速度;
2.如果估算准确的情况下,求方差时可直接借用上一步结果;
3.对于有规律的数据可用新方法口算得出结果。求平均数与方差:(1) 7, 8, 6 , 8 , 6 , 5 , 9 ,10,7,4
与7作差:0, 1,(-1),1 ,(-1),(-2), 2, 3 ,0,(-3)
作和 = 0,所以平均数为7
(2) 9 , 5 , 7 , 8 , 7 , 6 , 8 , 6 , 7, 7
与7作差:2 ,(-2), 0 , 1 , 0 ,(-1), 1 ,(-1), 0 , 0
作和= 0,所以平均数为7(3) 14 , 19 , 21 , 22 , 25 ,37,39,40,41,42
与30作差:(-16), (-11),(-9),(-8) ,(-5), 7 , 9,10,11,12
作和 = 0,所以平均数为30
(4) 16 , 16 , 16 , 27, 27,40,40,40,44,44
与30作差:(-14),(-14),(-14),(-3),(-3),10,10,10,14,14
作和 = 10,所以平均数为30 + 10÷10 = 31课堂小结:1.学会了怎样求平均数、方差与标准差。
2.学会了什么叫用样本的数字特征估计总体的数字特征,究竟用样本的数字特征估计总体的数字特征能解决什么实际问题。
3.学会了新的求平均数的方法。
完成课后案
教材 P70,练习 A 1,2
练习 B 1,2
作业:
