3.3.1 几何概型 课件(24张PPT)
文档属性
| 名称 | 3.3.1 几何概型 课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 252.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-29 00:00:00 | ||
图片预览







文档简介
课件24张PPT。几何概型(1)所有可能出现的基本事件只有有限个(有限性)
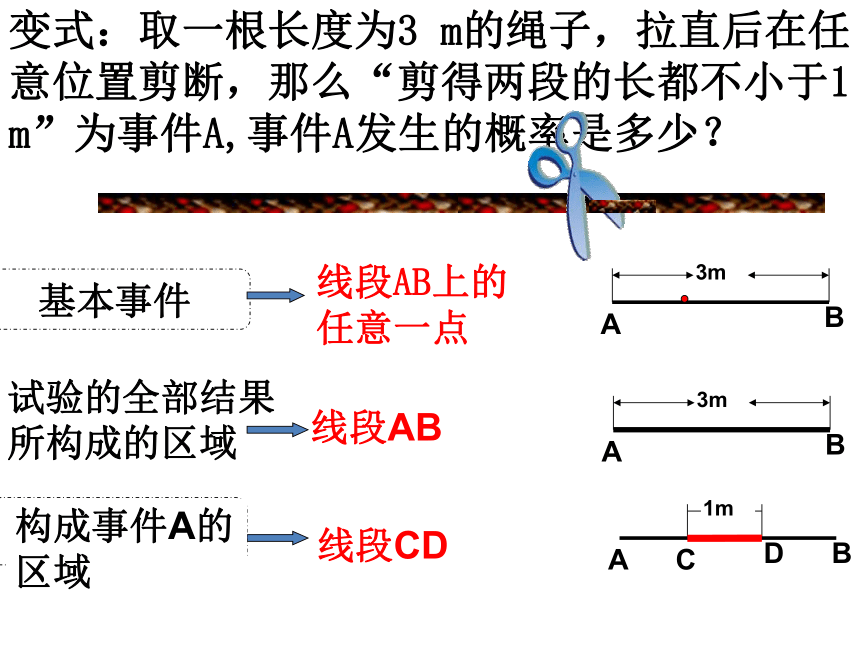
(2)每个基本事件出现的可能性相等(等可能性) 复习1.古典概型有哪些特点?2.古典概型的概率公式是什么?P(A)=A包含的基本事件的个数基本事件的总数创设情境 引入新课问题1:绳子上有均匀分布的10个点(如图),用剪刀随机的在A2----A9这8个点的位置剪,求剪刀剪在下标为偶数点的概率? 变式:取一根长度为3 m的绳子,拉直后在任意位置剪断,那么“剪得两段的长都不小于1 m”为事件A,事件A发生的概率是多少? 问题1:这个问题的基本事件是什么? 问题2:是否满足古典概型?如果不满足,为什么?
问题3:如何求事件A发生的概率?变式:取一根长度为3 m的绳子,拉直后在任意位置剪断,那么“剪得两段的长都不小于1 m”为事件A,事件A发生的概率是多少? 试验的全部结果所构成的区域构成事件A的区域创设情境 引入新课很多同学喜欢玩飞镖游戏,飞镖盘有圆形的,方形的,还有不规则图形的,丰富多彩的设计给这项运动增添了很多乐趣,同时也引出了一系列数学问题,下面我们来看看掷飞镖掷出的数学问题。问题2:如图,将圆盘等分成四个扇形区域,
现向圆盘投掷飞镖,假设飞镖都能射中圆盘,
且射中圆盘上的每一个扇形都是等可能的,
记“射中阴影区域”为事件A,则A发生的概率
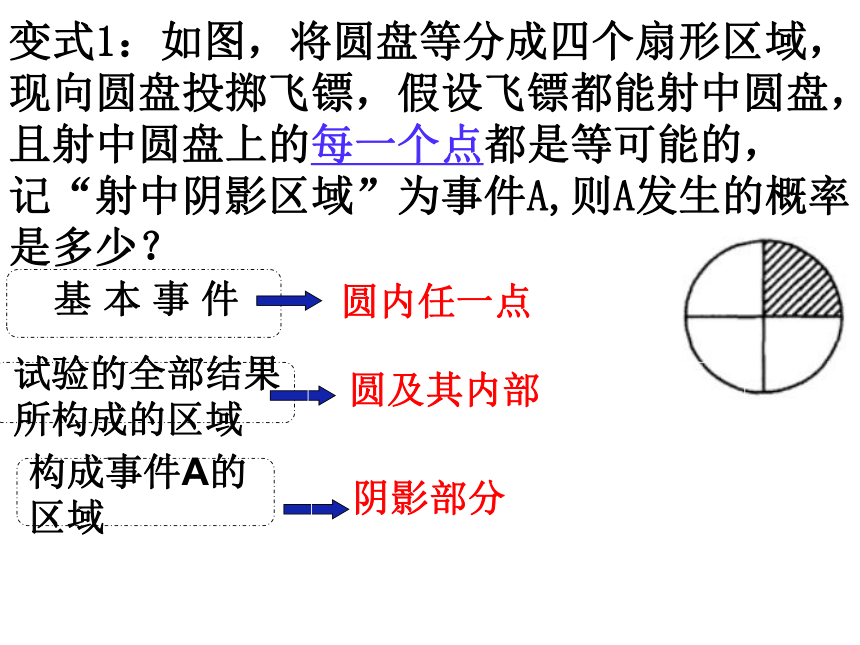
是多少?变式1:如图,将圆盘等分成四个扇形区域,
现向圆盘投掷飞镖,假设飞镖都能射中圆盘,
且射中圆盘上的每一个点都是等可能的,
记“射中阴影区域”为事件A,则A发生的概率
是多少?圆内任一点 圆及其内部构成事件A的区域 阴影部分变式2:如图,飞镖盘由两个面积为分别为
100cm2和400cm2的同心圆组成,现向圆盘投
掷飞镖,假设飞镖都能射中圆盘,且射中圆
盘上的每一个点都是等可能的,记“射中阴
影区域”为事件A,则A发生的概率是多少?
大圆内任一点大圆及其内部
小圆及其内部构成事件A的区域问题3:在一个边长为2m的盛满水的正方体容器中,一只小虫在容器中游动,记“它所在的位置距离正方体中心不超过1m”为事件A,那么事件A发生的概率是多少?正方体内任一点 正方体 半径为1的球及其内部构成事件A的区域小组讨论:
探究一:类比古典概型特点,说出以上概率问题有什么特点?
探究二:此概率模型中,事件A的概率计算公式是什么?⑴从一批产品中抽取30件进行检查,有5件次品,求正品的概率。
⑵箭靶的直径为1m,靶心的直径只有12cm,任意向靶射箭,求射中靶心的概率。
⑶从区间[0,1]上任取一个数,求这个数大于0.5的概率。
⑷在1万平方公里的海域中有40平方公里的大陆贮藏着石油.假如在海域中任意一点钻探,钻到油层面的概率是多少?古典概型练习:下列概率问题属于什么概型?几何概型几何概型几何概型例1 :△ABC中,三条边的长度分别为3、4、5,一只小蚂蚁在三角形的三条边上爬,记“小蚂蚁到三角形三个顶点的距离分别大于1”为事件A, 求事件A发生的概率。? 变式:△ABC中,三条边的长度分别为3、4、5,一只小蚂蚁在三角形及其内部里爬,记“小蚂蚁到三角形三个顶点的距离分别大于1”为事件B, 求事件B发生的概率。例2 :一海豚在水池中自由游弋,水池为长40米,宽30米的长方形。求此刻海豚嘴
尖离岸边不小5米的概率。
变式:一海豚在水池中自由玩耍,水池长40 m,宽30 m,高20m,求此海豚离池底和池壁均不小于5 m的概率。40m30m30m20m例3 某人午觉醒来,发现表停了,他打开收音机,想听电台报时(假设整点报时), 记“他等待的时间不多于10分钟”为事件A, 求事件的概
率.解:事件A恰好是打开收音机的时刻位于[50,60]时间段内发生。变式:在圆心角为90°的扇形中,以圆心0为起点作射线OC,则∠AOC和∠BOC都不小于30°的概率是( )A古典概型几何概型相同区别求解方法基本事件个数的有限性基本事件发生的等可能性基本事件发生的等可能性基本事件个数的无限性几何概型的概率公式. .(2016·全国乙卷) 某公司的班车在7:30 ,
8:00, 8:30发车,小明在7:50 至 8:30
之间到达发车站乘坐班车,且到达发车站的
时刻是随机的,则他等车时间不超过10分钟
的概率是( )B(2017全国1.理数.2)如图,正方形ABCD内
的图形来自中国古代的太极图.正方形内切圆
中的黑色部分和白色部分关于正方形的中心
成中心对称.在正方形内随机取一点,则此点
取自黑色部分的概率是( )B数学来源于生活,也应用于生活谢谢!例3 某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟
的概率.法1:(利用利用[50,60]时间段所占的弧长):解:设A={等待的时间不多于10分钟}.事件A恰好是打开收音机的时刻位于[50,60]时间段内发生。答:等待的时间不多于10分钟的概率为法2:(利用[50,60]时间段所占的圆心角):答:等待的时间不多于10分钟的概率为例3 某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟
的概率.解:设A={等待的时间不多于10分钟}.事件A恰好是打开收音机的时刻位于[50,60]时间段内发生。法3:(利用[50,60]时间段所占的面积):答:等待的时间不多于10分钟的概率为例3 某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟
的概率.解:设A={等待的时间不多于10分钟}.事件A恰好是打开收音机的时刻位于[50,60]时间段内发生。法4:(利用[50,60]时间段所占的线段长度):答:等待的时间不多于10分钟的概率为例3 某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟
的概率.解:设A={等待的时间不多于10分钟}.事件A恰好是打开收音机的时刻位于[50,60]时间段内发生。法四:将时间转化成长60的线段,研究事件A位于[50,60]之间的线段的概率:
(2)每个基本事件出现的可能性相等(等可能性) 复习1.古典概型有哪些特点?2.古典概型的概率公式是什么?P(A)=A包含的基本事件的个数基本事件的总数创设情境 引入新课问题1:绳子上有均匀分布的10个点(如图),用剪刀随机的在A2----A9这8个点的位置剪,求剪刀剪在下标为偶数点的概率? 变式:取一根长度为3 m的绳子,拉直后在任意位置剪断,那么“剪得两段的长都不小于1 m”为事件A,事件A发生的概率是多少? 问题1:这个问题的基本事件是什么? 问题2:是否满足古典概型?如果不满足,为什么?
问题3:如何求事件A发生的概率?变式:取一根长度为3 m的绳子,拉直后在任意位置剪断,那么“剪得两段的长都不小于1 m”为事件A,事件A发生的概率是多少? 试验的全部结果所构成的区域构成事件A的区域创设情境 引入新课很多同学喜欢玩飞镖游戏,飞镖盘有圆形的,方形的,还有不规则图形的,丰富多彩的设计给这项运动增添了很多乐趣,同时也引出了一系列数学问题,下面我们来看看掷飞镖掷出的数学问题。问题2:如图,将圆盘等分成四个扇形区域,
现向圆盘投掷飞镖,假设飞镖都能射中圆盘,
且射中圆盘上的每一个扇形都是等可能的,
记“射中阴影区域”为事件A,则A发生的概率
是多少?变式1:如图,将圆盘等分成四个扇形区域,
现向圆盘投掷飞镖,假设飞镖都能射中圆盘,
且射中圆盘上的每一个点都是等可能的,
记“射中阴影区域”为事件A,则A发生的概率
是多少?圆内任一点 圆及其内部构成事件A的区域 阴影部分变式2:如图,飞镖盘由两个面积为分别为
100cm2和400cm2的同心圆组成,现向圆盘投
掷飞镖,假设飞镖都能射中圆盘,且射中圆
盘上的每一个点都是等可能的,记“射中阴
影区域”为事件A,则A发生的概率是多少?
大圆内任一点大圆及其内部
小圆及其内部构成事件A的区域问题3:在一个边长为2m的盛满水的正方体容器中,一只小虫在容器中游动,记“它所在的位置距离正方体中心不超过1m”为事件A,那么事件A发生的概率是多少?正方体内任一点 正方体 半径为1的球及其内部构成事件A的区域小组讨论:
探究一:类比古典概型特点,说出以上概率问题有什么特点?
探究二:此概率模型中,事件A的概率计算公式是什么?⑴从一批产品中抽取30件进行检查,有5件次品,求正品的概率。
⑵箭靶的直径为1m,靶心的直径只有12cm,任意向靶射箭,求射中靶心的概率。
⑶从区间[0,1]上任取一个数,求这个数大于0.5的概率。
⑷在1万平方公里的海域中有40平方公里的大陆贮藏着石油.假如在海域中任意一点钻探,钻到油层面的概率是多少?古典概型练习:下列概率问题属于什么概型?几何概型几何概型几何概型例1 :△ABC中,三条边的长度分别为3、4、5,一只小蚂蚁在三角形的三条边上爬,记“小蚂蚁到三角形三个顶点的距离分别大于1”为事件A, 求事件A发生的概率。? 变式:△ABC中,三条边的长度分别为3、4、5,一只小蚂蚁在三角形及其内部里爬,记“小蚂蚁到三角形三个顶点的距离分别大于1”为事件B, 求事件B发生的概率。例2 :一海豚在水池中自由游弋,水池为长40米,宽30米的长方形。求此刻海豚嘴
尖离岸边不小5米的概率。
变式:一海豚在水池中自由玩耍,水池长40 m,宽30 m,高20m,求此海豚离池底和池壁均不小于5 m的概率。40m30m30m20m例3 某人午觉醒来,发现表停了,他打开收音机,想听电台报时(假设整点报时), 记“他等待的时间不多于10分钟”为事件A, 求事件的概
率.解:事件A恰好是打开收音机的时刻位于[50,60]时间段内发生。变式:在圆心角为90°的扇形中,以圆心0为起点作射线OC,则∠AOC和∠BOC都不小于30°的概率是( )A古典概型几何概型相同区别求解方法基本事件个数的有限性基本事件发生的等可能性基本事件发生的等可能性基本事件个数的无限性几何概型的概率公式. .(2016·全国乙卷) 某公司的班车在7:30 ,
8:00, 8:30发车,小明在7:50 至 8:30
之间到达发车站乘坐班车,且到达发车站的
时刻是随机的,则他等车时间不超过10分钟
的概率是( )B(2017全国1.理数.2)如图,正方形ABCD内
的图形来自中国古代的太极图.正方形内切圆
中的黑色部分和白色部分关于正方形的中心
成中心对称.在正方形内随机取一点,则此点
取自黑色部分的概率是( )B数学来源于生活,也应用于生活谢谢!例3 某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟
的概率.法1:(利用利用[50,60]时间段所占的弧长):解:设A={等待的时间不多于10分钟}.事件A恰好是打开收音机的时刻位于[50,60]时间段内发生。答:等待的时间不多于10分钟的概率为法2:(利用[50,60]时间段所占的圆心角):答:等待的时间不多于10分钟的概率为例3 某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟
的概率.解:设A={等待的时间不多于10分钟}.事件A恰好是打开收音机的时刻位于[50,60]时间段内发生。法3:(利用[50,60]时间段所占的面积):答:等待的时间不多于10分钟的概率为例3 某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟
的概率.解:设A={等待的时间不多于10分钟}.事件A恰好是打开收音机的时刻位于[50,60]时间段内发生。法4:(利用[50,60]时间段所占的线段长度):答:等待的时间不多于10分钟的概率为例3 某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟
的概率.解:设A={等待的时间不多于10分钟}.事件A恰好是打开收音机的时刻位于[50,60]时间段内发生。法四:将时间转化成长60的线段,研究事件A位于[50,60]之间的线段的概率:
