1.3.2 余弦函数、正切函数的图象与性质 课件(28张PPT)
文档属性
| 名称 | 1.3.2 余弦函数、正切函数的图象与性质 课件(28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 315.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-29 11:49:53 | ||
图片预览





文档简介
课件28张PPT。正切函数的定义与函数图象和性质tan(kπ+ )=_________(k∈Z);
tan(- )=_________;
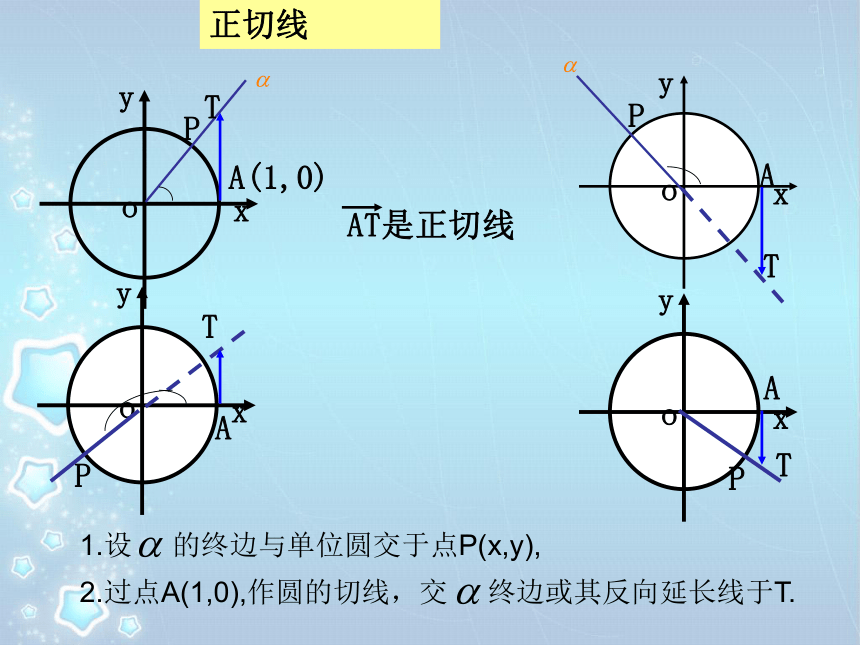
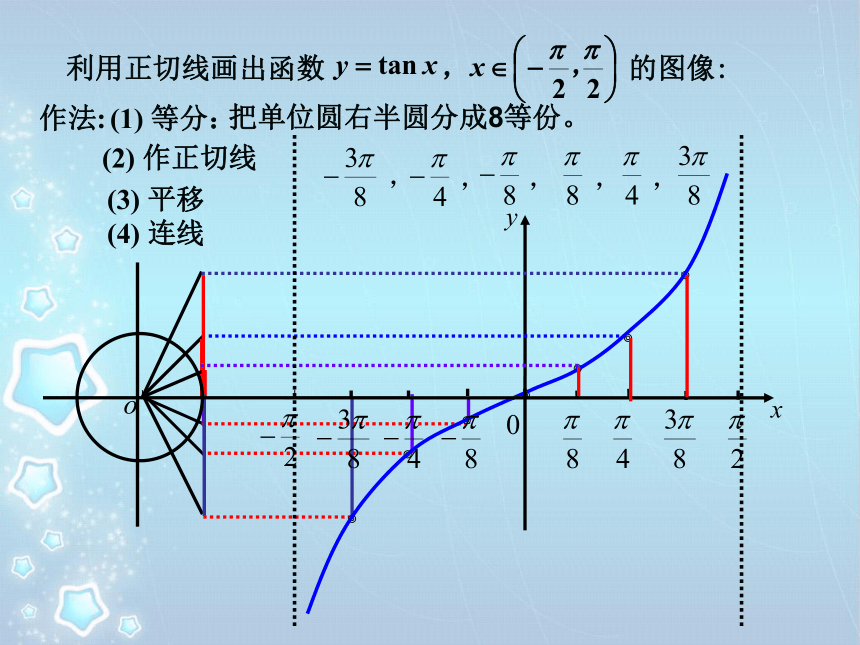
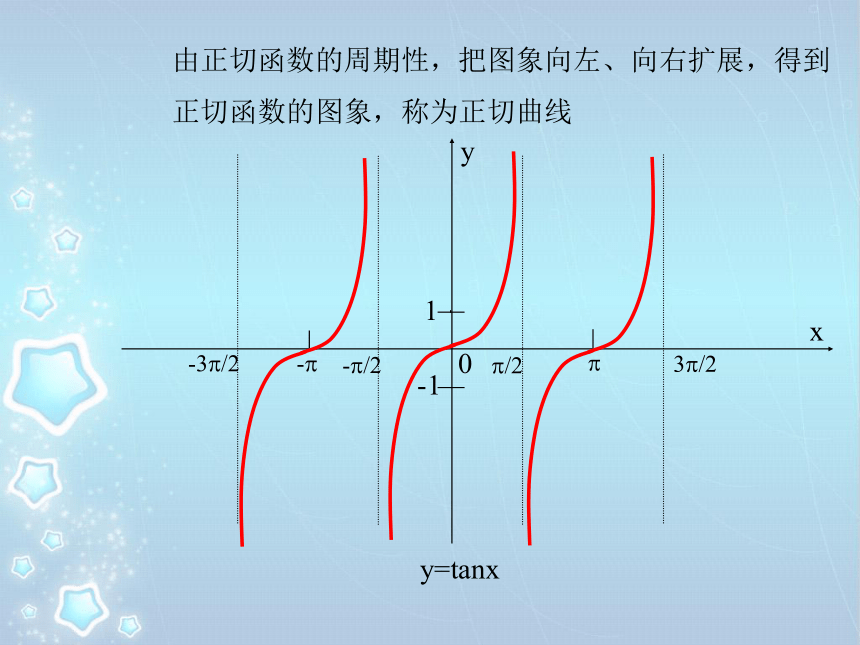
tan 有意义时, ∈______________________.复习旧知tan-tan利用正切函数的定义得到正切函数的有些性质:1、定义域:3、周期性:2、奇偶性:奇函数A(1,0)正切线PTPATPATPAT1.设 的终边与单位圆交于点P(x,y),2.过点A(1,0),作圆的切线,交 终边或其反向延长线于T.作法:(1) 等分:(2) 作正切线(3) 平移(4) 连线把单位圆右半圆分成8等份。利用正切线画出函数 , 的图像: 由正切函数的周期性,把图象向左、向右扩展,得到
正切函数的图象,称为正切曲线
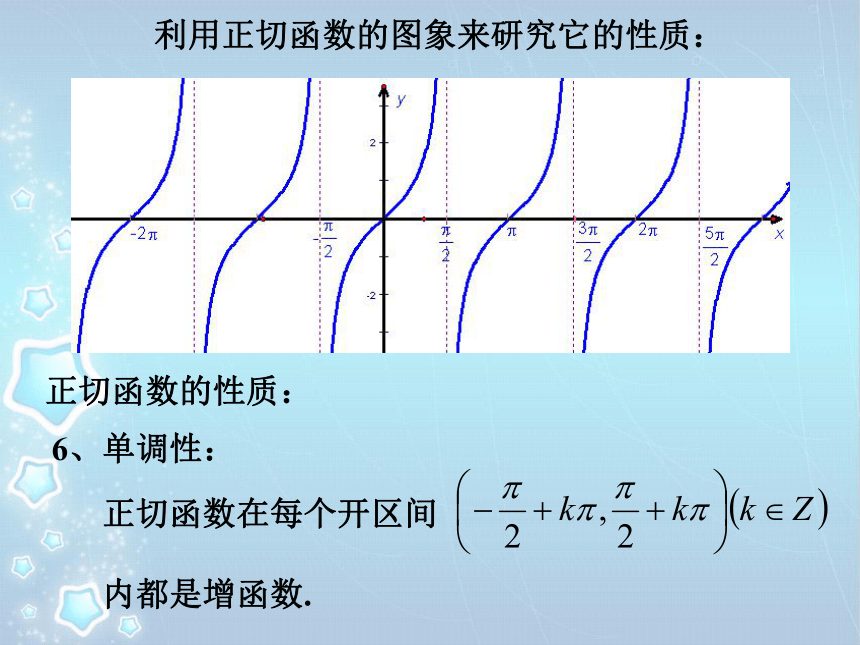
y=tanx利用正切函数的图象来研究它的性质:正切函数的性质:4、值域:当 小于 且无限接近于 时, 当 大于 且无限接近于 时, 对称中心为 ( )利用正切函数的图象来研究它的性质:正切函数的性质:5、对称性:利用正切函数的图象来研究它的性质:正切函数的性质:6、单调性:正切函数在每个开区间
内都是增函数.⑴ 定义域:(4)值域:⑶ 周期性:周期为(2)奇偶性: 在每一个开区间
, 内都是增函数。正
切
函
数
图
像奇函数,图象关于原点对称。R,无最值.⑸ 单调性:(6)对称中心思考与讨论:正切函数是整个定义域上的增函
数吗?为什么?不是.取,x1= , x2= ,显然x1< x2,但y1=tan =1
y2=tan = ,y1>y2,不符合增函数定义.四、性质应用:例1.比较大小.
(1)tan ____tan ; (2)tan( )____tan( );
(3)tan1____tan4.解:(1)∵ < < < ,且y=tanx在区间 ( , )
上是增函数.∴tan < tan(2) tan( ) = tan( ) ,tan( )=tan( ) ∵ < < < ,且y=tanx在区间 ( , )
上是增函数.∴tan < tan∴tan < tan四、性质应用:例1.比较大小.
(1)tan ____tan ; (2)tan( )____tan( );
(3)tan1____tan4. ∵ < < < ,且y=tanx在区间 ( , )
上是增函数.∴tan1> tan4(3) tan4= tan( 4 ) 解:∴tan1> tan跟踪练习:比较大小.
(1)tan ____tan ; (2)tan138 ____tan143 ><
例2:观察正切曲线,写出满足下列条件的x的值的范围。
(1) tanx >0 (2)tanx <1(k?,k?+?/2) k?z(k?–?/2,k?+?/4)k?z跟踪练习: 观察正切曲线,写出满足下列条件的x的值的范围。
(1) 1+tanx 0 (2)tanx [k?- ?/4,k?+ ?/2 ) ,(k?z)(k?–?/2,k?+?/3] ,(k?z)例3.判断函数f(x) = -tanx , x R且x
的奇偶性.又∵f(-x)=-tan(-x)=tanx=-f(x)∴f(x)是奇函数.判断函数f(x) = |tanx |, x R且x
的奇偶性. 跟踪练习:偶函数例4.求函数 的定义域. 解: 令 ,那么函数 的定义域是: 所以函数 的定义域是 由 ,可得
跟踪练习:求函数y = -tan(x+ )+2的定义域. 例5.求函数y=tan( )的单调区间. 所以函数y=tan( )的单调增区
间是( ), .跟踪练习:求函数y=tan(x+ )的单调区间和对称中心. 增区间:例6.求函数y=tan3x的周期.解:因为tan(3x+π)=tan3x,即tan3(x+π/3 )=tan3x这说明自变量x至少增加π/3 ,函数值
才能重复取得,所以,函数y=tan3x的周
期为π/3 .结论函数y=Atan( ) , 的周期
T=______.例7.(1)作函数y=tan(2x+ )的简图.00-11例7.(2)函数y=tan(2x+ )是由y=tanx如何变换得到的?向左平移 个单位横坐标缩短到原来的1/2倍(纵坐标不变)横坐标缩短到原来的1/2倍(纵坐标不变)向左平移 个单位跟踪练习:函数y=tan( ) 在一个周期内的图象是( )A动手试试:
tan(- )=_________;
tan 有意义时, ∈______________________.复习旧知tan-tan利用正切函数的定义得到正切函数的有些性质:1、定义域:3、周期性:2、奇偶性:奇函数A(1,0)正切线PTPATPATPAT1.设 的终边与单位圆交于点P(x,y),2.过点A(1,0),作圆的切线,交 终边或其反向延长线于T.作法:(1) 等分:(2) 作正切线(3) 平移(4) 连线把单位圆右半圆分成8等份。利用正切线画出函数 , 的图像: 由正切函数的周期性,把图象向左、向右扩展,得到
正切函数的图象,称为正切曲线
y=tanx利用正切函数的图象来研究它的性质:正切函数的性质:4、值域:当 小于 且无限接近于 时, 当 大于 且无限接近于 时, 对称中心为 ( )利用正切函数的图象来研究它的性质:正切函数的性质:5、对称性:利用正切函数的图象来研究它的性质:正切函数的性质:6、单调性:正切函数在每个开区间
内都是增函数.⑴ 定义域:(4)值域:⑶ 周期性:周期为(2)奇偶性: 在每一个开区间
, 内都是增函数。正
切
函
数
图
像奇函数,图象关于原点对称。R,无最值.⑸ 单调性:(6)对称中心思考与讨论:正切函数是整个定义域上的增函
数吗?为什么?不是.取,x1= , x2= ,显然x1< x2,但y1=tan =1
y2=tan = ,y1>y2,不符合增函数定义.四、性质应用:例1.比较大小.
(1)tan ____tan ; (2)tan( )____tan( );
(3)tan1____tan4.解:(1)∵ < < < ,且y=tanx在区间 ( , )
上是增函数.∴tan < tan(2) tan( ) = tan( ) ,tan( )=tan( ) ∵ < < < ,且y=tanx在区间 ( , )
上是增函数.∴tan < tan∴tan < tan四、性质应用:例1.比较大小.
(1)tan ____tan ; (2)tan( )____tan( );
(3)tan1____tan4. ∵ < < < ,且y=tanx在区间 ( , )
上是增函数.∴tan1> tan4(3) tan4= tan( 4 ) 解:∴tan1> tan跟踪练习:比较大小.
(1)tan ____tan ; (2)tan138 ____tan143 ><
例2:观察正切曲线,写出满足下列条件的x的值的范围。
(1) tanx >0 (2)tanx <1(k?,k?+?/2) k?z(k?–?/2,k?+?/4)k?z跟踪练习: 观察正切曲线,写出满足下列条件的x的值的范围。
(1) 1+tanx 0 (2)tanx [k?- ?/4,k?+ ?/2 ) ,(k?z)(k?–?/2,k?+?/3] ,(k?z)例3.判断函数f(x) = -tanx , x R且x
的奇偶性.又∵f(-x)=-tan(-x)=tanx=-f(x)∴f(x)是奇函数.判断函数f(x) = |tanx |, x R且x
的奇偶性. 跟踪练习:偶函数例4.求函数 的定义域. 解: 令 ,那么函数 的定义域是: 所以函数 的定义域是 由 ,可得
跟踪练习:求函数y = -tan(x+ )+2的定义域. 例5.求函数y=tan( )的单调区间. 所以函数y=tan( )的单调增区
间是( ), .跟踪练习:求函数y=tan(x+ )的单调区间和对称中心. 增区间:例6.求函数y=tan3x的周期.解:因为tan(3x+π)=tan3x,即tan3(x+π/3 )=tan3x这说明自变量x至少增加π/3 ,函数值
才能重复取得,所以,函数y=tan3x的周
期为π/3 .结论函数y=Atan( ) , 的周期
T=______.例7.(1)作函数y=tan(2x+ )的简图.00-11例7.(2)函数y=tan(2x+ )是由y=tanx如何变换得到的?向左平移 个单位横坐标缩短到原来的1/2倍(纵坐标不变)横坐标缩短到原来的1/2倍(纵坐标不变)向左平移 个单位跟踪练习:函数y=tan( ) 在一个周期内的图象是( )A动手试试:
