1.2.1 三角函数的定义 课件(24张PPT)
文档属性
| 名称 | 1.2.1 三角函数的定义 课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-29 11:51:23 | ||
图片预览






文档简介
课件24张PPT。普通高中课程标准实验教科书
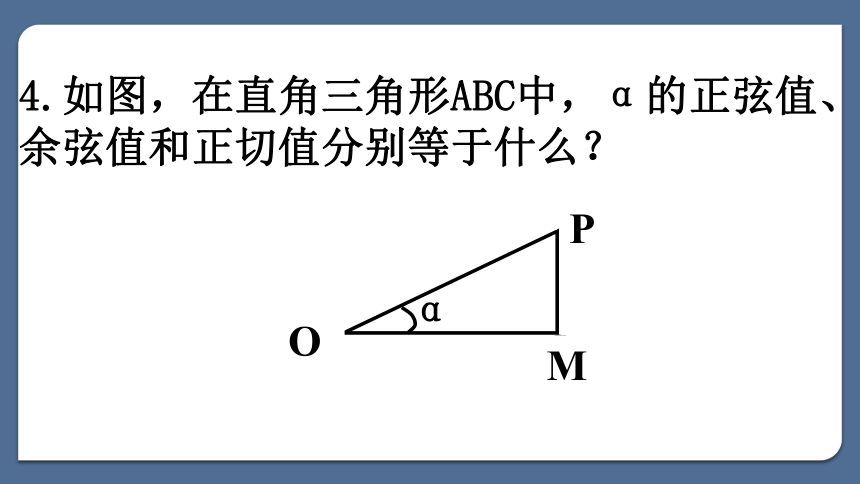
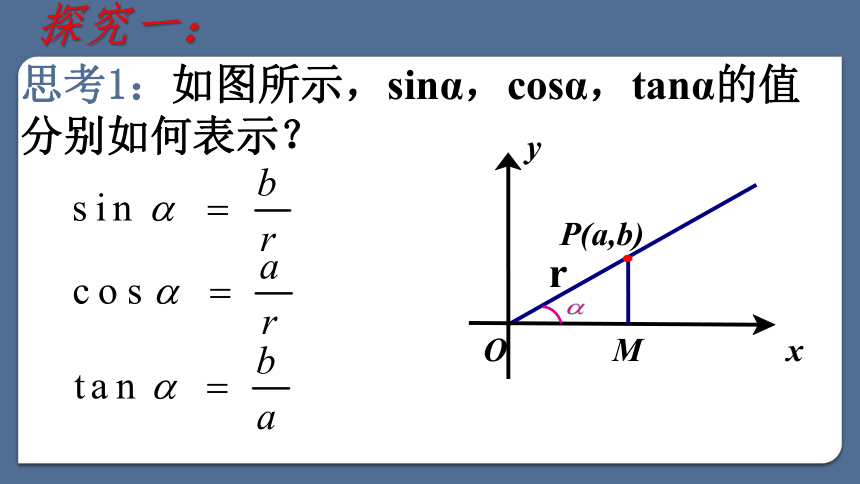
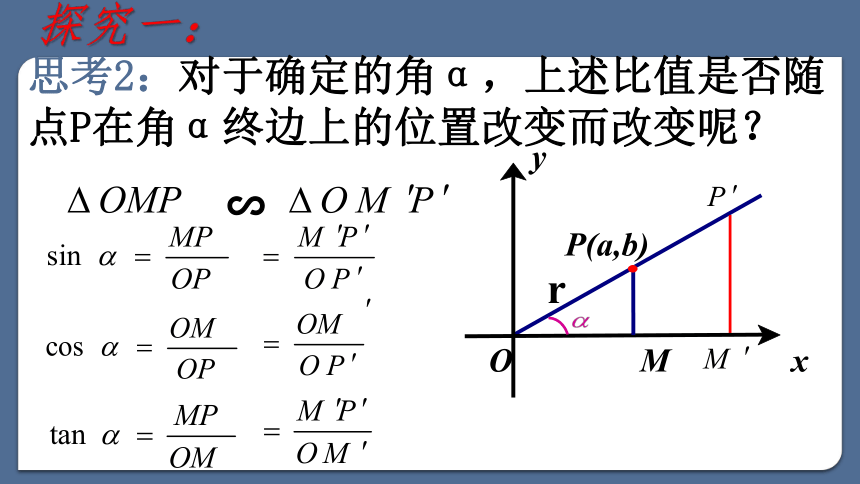
(人教版数学必修四) 《任意角的三角函数》问题提出1.角的理解:(1)角是由平面内一条射线绕其端点从一个位置旋转到另一个位置所组成的图形.(2)按逆时针方向旋转形成的角为正角,按顺时针方向旋转形成的角为负角,没有作任何旋转形成的角为零角.(3)角的大小是任意的.2.什么叫做1弧度的角?度与弧度是怎样换算的?(1)等于半径长的圆弧所对的圆心角叫做1弧度的角. 3. 与角α终边相同的角的一般表达式是什么?β=α+k·360°(k∈Z)或 β=α+2kπ(k∈Z)(2)180°= πrad.OPM4.如图,在直角三角形ABC中,α的正弦值、余弦值和正切值分别等于什么?任意角三角函数探究一:任意角三角函数思考1:如图所示,sinα,cosα,tanα的值分别如何表示?探究一:MOyxP(a,b)r思考2:对于确定的角α,上述比值是否随点P在角α终边上的位置改变而改变呢? MOyxP(a,b)r∽探究一:思考3:怎样使sinα ,cosα,tanα的表示式更简单?探究一:思考4:对于角α的终边上一点P,要使|OP|=1,点P的位置如何确定? 探究一:思考5:设α是一个任意角,它的终边与单位圆交于点P(x,y),sinα,cosα,tanα对应的值应分别如何定义? 探究一:思考6:对于一个任意给定的角α,按照上述定义,对应的sinα,cosα,tanα的值是否存在?是否惟一?对应关系 , , 都是以角为自变量,以单位圆上的点的坐标或坐标的比值为函数值的函数,分别称为正弦函数、余弦函数和正切函数,并统称为三角函数.探究一:思考6:对于一个任意给定的角α,按照上述定义,对应的sinα,cosα,tanα的值是否存在?是否惟一?思考6:对于一个任意给定的角α,按照上述定义,对应的sinα,cosα,tanα的值是否存在?是否唯一?探究一:思考6:对于一个任意给定的角α,按照上述定义,对应的sinα,cosα,tanα的值是否存在?是否惟一?正切函数的定义域为 正、余弦函数的定义域为R,思考7:在弧度制中,这三个三角函数的定义域分别是什么?探究一:思考6:对于一个任意给定的角α,按照上述定义,对应的sinα,cosα,tanα的值是否存在?是否惟一?思考8:若点P(x,y)为角α终边上任意一点,那么sinα,cosα,tanα对应的函数值分别等于什么?探究一:例1 已知角α的终边经过点P(-3,-4),求角α的正弦、余弦和正切值 。例2 求 的正弦,余弦,正切值。OM
探究二:三角函数值符号思考6:对于一个任意给定的角α,按照上述定义,对应的sinα,cosα,tanα的值是否存在?是否惟一?讨论:当角α在某个象限时,设其终边与单位圆交于点P(x,y),根据三角函数定义,sinα,cosα,tanα的函数值符号是否确定?为什么?一全正,二正弦,三正切,四余弦。探究二:例4 已知sinθ和cosθ异号,
θ为第 二、四象限角. ____ 例3 确定下列三角函数值的符号.
① sin324° ② cos(-89°)
③ tan π
我学到了什么?假设摩天轮逆时针匀速转动,尝试用本节课所学知识建立数学模型,求出游客所乘坐的客舱相对于地面的高度与时间之间的关系式。
数学与生活临 江 市 第 一 中 学
(人教版数学必修四) 《任意角的三角函数》问题提出1.角的理解:(1)角是由平面内一条射线绕其端点从一个位置旋转到另一个位置所组成的图形.(2)按逆时针方向旋转形成的角为正角,按顺时针方向旋转形成的角为负角,没有作任何旋转形成的角为零角.(3)角的大小是任意的.2.什么叫做1弧度的角?度与弧度是怎样换算的?(1)等于半径长的圆弧所对的圆心角叫做1弧度的角. 3. 与角α终边相同的角的一般表达式是什么?β=α+k·360°(k∈Z)或 β=α+2kπ(k∈Z)(2)180°= πrad.OPM4.如图,在直角三角形ABC中,α的正弦值、余弦值和正切值分别等于什么?任意角三角函数探究一:任意角三角函数思考1:如图所示,sinα,cosα,tanα的值分别如何表示?探究一:MOyxP(a,b)r思考2:对于确定的角α,上述比值是否随点P在角α终边上的位置改变而改变呢? MOyxP(a,b)r∽探究一:思考3:怎样使sinα ,cosα,tanα的表示式更简单?探究一:思考4:对于角α的终边上一点P,要使|OP|=1,点P的位置如何确定? 探究一:思考5:设α是一个任意角,它的终边与单位圆交于点P(x,y),sinα,cosα,tanα对应的值应分别如何定义? 探究一:思考6:对于一个任意给定的角α,按照上述定义,对应的sinα,cosα,tanα的值是否存在?是否惟一?对应关系 , , 都是以角为自变量,以单位圆上的点的坐标或坐标的比值为函数值的函数,分别称为正弦函数、余弦函数和正切函数,并统称为三角函数.探究一:思考6:对于一个任意给定的角α,按照上述定义,对应的sinα,cosα,tanα的值是否存在?是否惟一?思考6:对于一个任意给定的角α,按照上述定义,对应的sinα,cosα,tanα的值是否存在?是否唯一?探究一:思考6:对于一个任意给定的角α,按照上述定义,对应的sinα,cosα,tanα的值是否存在?是否惟一?正切函数的定义域为 正、余弦函数的定义域为R,思考7:在弧度制中,这三个三角函数的定义域分别是什么?探究一:思考6:对于一个任意给定的角α,按照上述定义,对应的sinα,cosα,tanα的值是否存在?是否惟一?思考8:若点P(x,y)为角α终边上任意一点,那么sinα,cosα,tanα对应的函数值分别等于什么?探究一:例1 已知角α的终边经过点P(-3,-4),求角α的正弦、余弦和正切值 。例2 求 的正弦,余弦,正切值。OM
探究二:三角函数值符号思考6:对于一个任意给定的角α,按照上述定义,对应的sinα,cosα,tanα的值是否存在?是否惟一?讨论:当角α在某个象限时,设其终边与单位圆交于点P(x,y),根据三角函数定义,sinα,cosα,tanα的函数值符号是否确定?为什么?一全正,二正弦,三正切,四余弦。探究二:例4 已知sinθ和cosθ异号,
θ为第 二、四象限角. ____ 例3 确定下列三角函数值的符号.
① sin324° ② cos(-89°)
③ tan π
我学到了什么?假设摩天轮逆时针匀速转动,尝试用本节课所学知识建立数学模型,求出游客所乘坐的客舱相对于地面的高度与时间之间的关系式。
数学与生活临 江 市 第 一 中 学
