1.2.1 三角函数的定义 课件(30张PPT)
文档属性
| 名称 | 1.2.1 三角函数的定义 课件(30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-29 11:50:38 | ||
图片预览









文档简介
课件30张PPT。1.2.1 三角函数的定义第一章 §1.2 任意角的三角函数学习目标:
1.理解任意角的三角函数的定义。
2.掌握三角函数在各个象限的符号。
3.掌握正弦、余弦、正切函数的定义域。回顾一:前几节课所讲,角的概念的推广。角的概念的推广:一条射线绕着它的端点旋转所形成的图形叫做角,我们通常把逆时针旋转的角称为正角,顺时针旋转的角称为负角,如果没有进行旋转,成为零角。
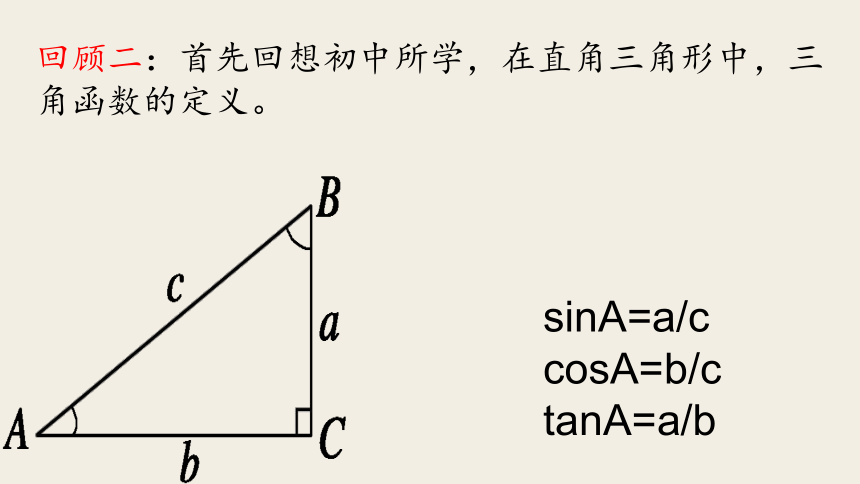
这节课我们就来研究一下任意角的三角函数回顾二:首先回想初中所学,在直角三角形中,三角函数的定义。sinA=a/c
cosA=b/c
tanA=a/b
思考:角α的正弦、余弦、正切分别等于什么?将直角三角形放在直角坐标系中来研究:使锐角α的顶点与原点O重合,始边与x轴的非负半轴重合,在终边上任取一点P,作PM⊥x轴于M,设P(x,y),|OP|=r. 思考:对确定的锐角α,sin α,cos α,tan α的值是否随P点在终边上的位置的改变而改变?答案 不会。因为三角函数值是比值,其大小与点P(x,y)在终边上的位置无关。如图,设P(x,y)是角α终边上不同于坐标原点的任意一点,设OP=r(r≠0).
(1)定义
余弦:cos α =
正弦:sin α =
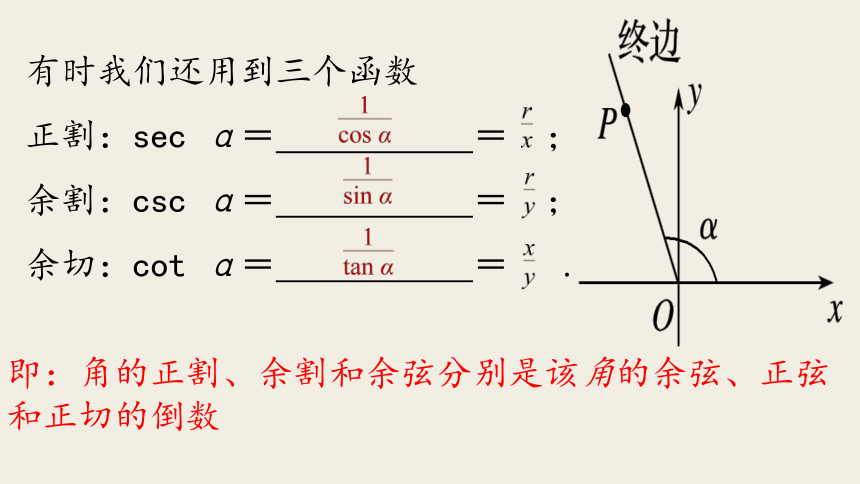
正切:tan α =推广得出任意角的三角函数的定义有时我们还用到三个函数
正割:sec α= = ;
余割:csc α= = ;
余切:cot α= = .即:角的正割、余割和余弦分别是该角的余弦、正弦和正切的倒数思考:对于任意角α,sin α,cos α,tan α都有意义吗?答案:由三角函数的定义可知,对于任意角α,sin α,cos α都有意义,而当角α的终边在y轴上时,任取一点P,其横坐标x都为0,此时 无意义,故tan α无意义。三角函数的定义域 思考:根据三角函数的定义,你能判断正弦、余弦、正切函数的值在各象限的符号吗? 分析:由三角函数的定义可知,三角函数的符号取决于x,y的符号。
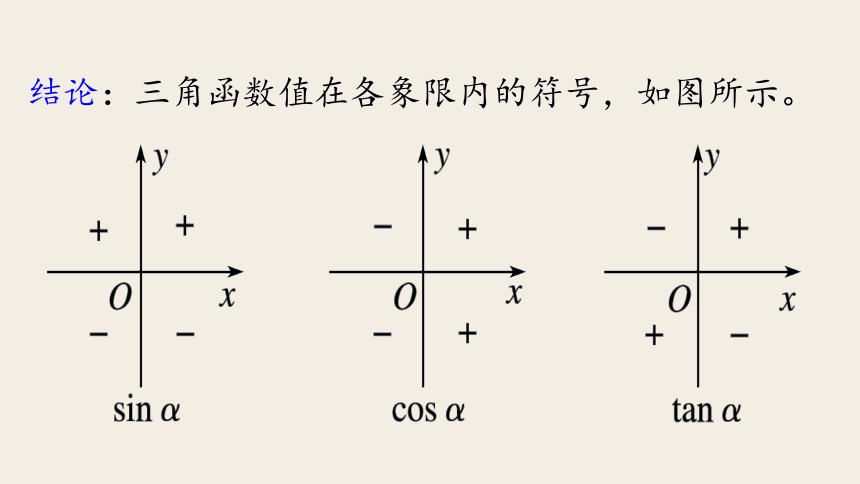
即:余弦的符号与x的符号相同
正弦的符号与y的符号相同
正切的符号由x,y共同决定结论:三角函数值在各象限内的符号,如图所示。例1:已知角α的终边经过点P(2,-3),求α的六个三角函数值.题型一:三角函数定义的应用解:因为x=2,y=-3,
训练例2:已知角α的终边过点P(-3a,4a)(a≠0),求2sin α+cos α的值.①若a>0,则r=5a,角α在第二象限,②若a<0,则r=-5a,角α在第四象限,综上所述,2sin α+cos α=±1.训练2:已知角α的终边落在直线 x+y=0上,求sin α,cos α,tan α,sec α,csc α,cot α的值.例3 (1)确定下列各三角函数值的符号.
①sin 182°;
解 ∵182°是第三象限角,
∴sin 182°是负的,符号是“-”.
②cos(-43°);
解 ∵-43°是第四象限角,
∴cos(-43°)是正的,符号是“+”.题型二:三角函数值符号的判断∴sin 3>0,cos 4<0,tan 5<0,
∴sin 3·cos 4·tan 5>0.②sin 3·cos 4·tan 5(2)若α是第二象限角,则点P(sinα,cosα)在
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析 ∵α为第二象限角,
∴sin α>0,cos α<0,
∴点P在第四象限,故选D.训练3:(1)判断下列各式的符号.
①sin 145°cos(-210°);
解 ∵145°是第二象限角,∴sin 145°>0.
∵-210°=-360°+150°,∴-210°是第二象限角,
∴cos (-210°)<0,∴sin 145°cos(-210°)<0.(2)已知点P(tan α,cos α)在第三象限,则α是第 象限角.
解析 由题意知tan α<0,cos α<0,
∴α是第二象限角.二小试身手1.已知角α的终边经过点(-4,3),则cos α等于解析 由题意可知,x=-4,y=3,r=5,2.若点P(3,y)是角α终边上的一点,且满足y<0,cos α= ,则tan α等于故选DA.1 B.0
C.2 D.-2解析 ∵α为第二象限角,∴sin α>0,cos α<0.35.已知角α的终边上有一点P(24k,7k),k≠0,求sin α,cos α,tan α的值.解 当k>0时,令x=24k,y=7k,当k<0时,令x=24k,y=7k,则有r=-25k,4课堂小结
本节课我们学习了
1、任意角三角函数的定义。
2、讨论了正弦、余弦、正切函数的定义域。
3、三角函数在各象限内的符号。本课结束
1.理解任意角的三角函数的定义。
2.掌握三角函数在各个象限的符号。
3.掌握正弦、余弦、正切函数的定义域。回顾一:前几节课所讲,角的概念的推广。角的概念的推广:一条射线绕着它的端点旋转所形成的图形叫做角,我们通常把逆时针旋转的角称为正角,顺时针旋转的角称为负角,如果没有进行旋转,成为零角。
这节课我们就来研究一下任意角的三角函数回顾二:首先回想初中所学,在直角三角形中,三角函数的定义。sinA=a/c
cosA=b/c
tanA=a/b
思考:角α的正弦、余弦、正切分别等于什么?将直角三角形放在直角坐标系中来研究:使锐角α的顶点与原点O重合,始边与x轴的非负半轴重合,在终边上任取一点P,作PM⊥x轴于M,设P(x,y),|OP|=r. 思考:对确定的锐角α,sin α,cos α,tan α的值是否随P点在终边上的位置的改变而改变?答案 不会。因为三角函数值是比值,其大小与点P(x,y)在终边上的位置无关。如图,设P(x,y)是角α终边上不同于坐标原点的任意一点,设OP=r(r≠0).
(1)定义
余弦:cos α =
正弦:sin α =
正切:tan α =推广得出任意角的三角函数的定义有时我们还用到三个函数
正割:sec α= = ;
余割:csc α= = ;
余切:cot α= = .即:角的正割、余割和余弦分别是该角的余弦、正弦和正切的倒数思考:对于任意角α,sin α,cos α,tan α都有意义吗?答案:由三角函数的定义可知,对于任意角α,sin α,cos α都有意义,而当角α的终边在y轴上时,任取一点P,其横坐标x都为0,此时 无意义,故tan α无意义。三角函数的定义域 思考:根据三角函数的定义,你能判断正弦、余弦、正切函数的值在各象限的符号吗? 分析:由三角函数的定义可知,三角函数的符号取决于x,y的符号。
即:余弦的符号与x的符号相同
正弦的符号与y的符号相同
正切的符号由x,y共同决定结论:三角函数值在各象限内的符号,如图所示。例1:已知角α的终边经过点P(2,-3),求α的六个三角函数值.题型一:三角函数定义的应用解:因为x=2,y=-3,
训练例2:已知角α的终边过点P(-3a,4a)(a≠0),求2sin α+cos α的值.①若a>0,则r=5a,角α在第二象限,②若a<0,则r=-5a,角α在第四象限,综上所述,2sin α+cos α=±1.训练2:已知角α的终边落在直线 x+y=0上,求sin α,cos α,tan α,sec α,csc α,cot α的值.例3 (1)确定下列各三角函数值的符号.
①sin 182°;
解 ∵182°是第三象限角,
∴sin 182°是负的,符号是“-”.
②cos(-43°);
解 ∵-43°是第四象限角,
∴cos(-43°)是正的,符号是“+”.题型二:三角函数值符号的判断∴sin 3>0,cos 4<0,tan 5<0,
∴sin 3·cos 4·tan 5>0.②sin 3·cos 4·tan 5(2)若α是第二象限角,则点P(sinα,cosα)在
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析 ∵α为第二象限角,
∴sin α>0,cos α<0,
∴点P在第四象限,故选D.训练3:(1)判断下列各式的符号.
①sin 145°cos(-210°);
解 ∵145°是第二象限角,∴sin 145°>0.
∵-210°=-360°+150°,∴-210°是第二象限角,
∴cos (-210°)<0,∴sin 145°cos(-210°)<0.(2)已知点P(tan α,cos α)在第三象限,则α是第 象限角.
解析 由题意知tan α<0,cos α<0,
∴α是第二象限角.二小试身手1.已知角α的终边经过点(-4,3),则cos α等于解析 由题意可知,x=-4,y=3,r=5,2.若点P(3,y)是角α终边上的一点,且满足y<0,cos α= ,则tan α等于故选DA.1 B.0
C.2 D.-2解析 ∵α为第二象限角,∴sin α>0,cos α<0.35.已知角α的终边上有一点P(24k,7k),k≠0,求sin α,cos α,tan α的值.解 当k>0时,令x=24k,y=7k,当k<0时,令x=24k,y=7k,则有r=-25k,4课堂小结
本节课我们学习了
1、任意角三角函数的定义。
2、讨论了正弦、余弦、正切函数的定义域。
3、三角函数在各象限内的符号。本课结束
