1.1.1 角的概念的推广 课件(24张PPT)
文档属性
| 名称 | 1.1.1 角的概念的推广 课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-29 00:00:00 | ||
图片预览








文档简介
课件24张PPT。第一章 三角函数
1.1 角的概念的推广1.结合具体实例,认识角的推广的必要性.
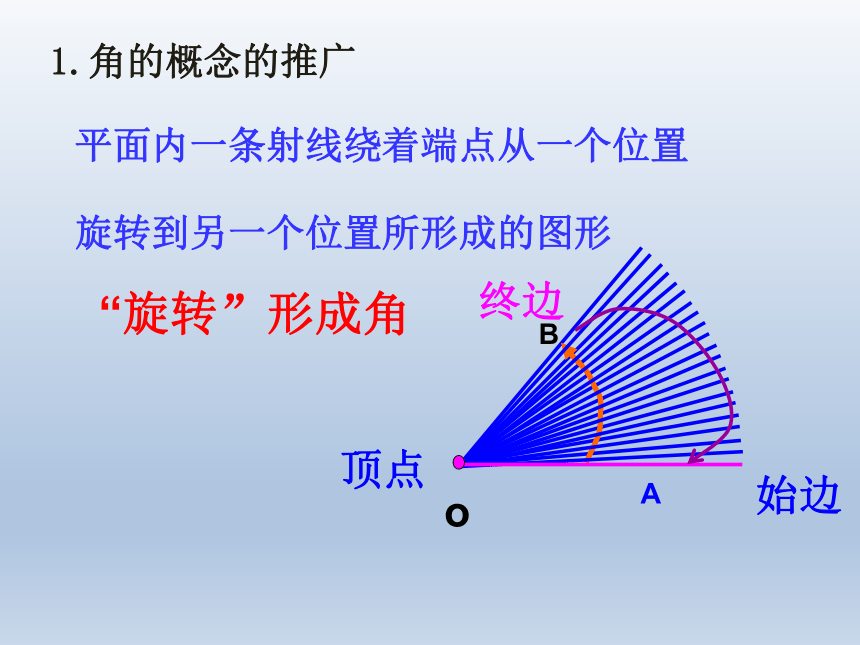
2.初步学会在平面直角坐标系中讨论任意角,并能熟练写出与已知角终边相同的角的集合.2.初中学习的角的范围? 0o<α≤360o想一想生活中是不是只有这些角呢?1.初中所学角是如何定义的?具有公共顶点的两条射线组成的图形跳水运动员向内、向外转体两周,这是多大角度? 自行车的车轮周而复始地转动形成角 钟表转动一圈又一圈形成的角“旋转”形成角 平面内一条射线绕着端点从一个位置
旋转到另一个位置所形成的图形1.角的概念的推广规定:
(1)按逆时针方向旋转形成的角叫做正角;
(2)按顺时针方向旋转形成的角叫做负角
(3)如果一条射线没有作任何旋转,则称它形成了一个零角.记作α=0o.这样,我们就把角的概念推广到了任意角.探究一:如果你的手表慢了20分钟,或快了1小时,你应该将分钟分别旋转多少度才能
将时间校准?—120°,360°.B1γAB2αOB3y二、象限角x 为了进一步研究角的需要,我们常在直角坐标系内讨论角,并使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么对一个任意角,角的终边可能落在哪些位置? 口答:
-50°,405°,210°, -200°
分别是第几象限的角?第四象限角第一象限角第三象限角第二象限角探究二:在直角坐标系中,给
定一个角,这个角的终边唯一
确定,若给一条射线作终边,
这个角唯一吗?1.在直角坐标系中画出-30°,330°,
-390°, 这些角有什么内在联系?-32°-390°o330°, {β︱β= -30°+ k·360°,k∈Z}归纳:与-30°角终边相同的角330°=-30°+360°-390°=-30°+(-1)×360° 一般地,所有与角α终边相同的角,
连同角α在内,可构成一个集合 S={β︱β=α+k·360°,k∈Z}三、终边相同的角 练习1:写出与30°,45°,—60°终边相同的角的集合{β︱β=45 °+ k·360°,k∈Z}{β︱β=30 °+ k·360°,k∈Z}{β︱β=-60 °+ k·360°,k∈Z}例1 写出终边在y轴的角的集合.解:在0°~360°范围内,终边在y轴上的角有两
个,即90°,270°角(图1.1-6).因此,所有与
90°角终边相同的角构成集合
S1={β|β=90°+k·360°.k∈Z}.
而所有与270°角终边相同的角构成集合
S2={β|β=270°+k·360°.k∈Z}.于是,终边在y轴上的角的集合
S=S1∪S2
={β|β=90°+2k·180°,k∈Z }
∪{β|β=90°+180°+2k·180°,k∈Z }
={β|β=90°+2k·180°,k∈Z }
∪{β|β=90°+(2k+1)180°,k∈Z }
={β|β=90°+n·180°,n∈Z }例题2. 在0o到360o范围内,找出与下列各角终边相同的角,并判断它是哪个象限的角.
(1) -120o; (2) 640o;解:⑴∵-120o=-360o+240o,
∴240o的角与-120o的角终边相同,
它是第三象限角.
⑵ ∵640o=360o+280o,
∴280o的角与640o的角终边相同,
它是第四象限角. 学生活动:
1.锐角是第几象限?第一象限角一定是锐角吗?
2.钝角是第几象限?第二象限角一定是钝角?
3.直角是第几象限?轴线角一定是直角?
锐角一定是第一象限的角,第一象限角不一定是锐角.钝角一定是第二象限的角,第二象限角不一定是钝角.直角一定是轴线角,轴线角不一定是直角.正角
负角
零角象限角
轴线角终边相同角角谢谢大家
1.1 角的概念的推广1.结合具体实例,认识角的推广的必要性.
2.初步学会在平面直角坐标系中讨论任意角,并能熟练写出与已知角终边相同的角的集合.2.初中学习的角的范围? 0o<α≤360o想一想生活中是不是只有这些角呢?1.初中所学角是如何定义的?具有公共顶点的两条射线组成的图形跳水运动员向内、向外转体两周,这是多大角度? 自行车的车轮周而复始地转动形成角 钟表转动一圈又一圈形成的角“旋转”形成角 平面内一条射线绕着端点从一个位置
旋转到另一个位置所形成的图形1.角的概念的推广规定:
(1)按逆时针方向旋转形成的角叫做正角;
(2)按顺时针方向旋转形成的角叫做负角
(3)如果一条射线没有作任何旋转,则称它形成了一个零角.记作α=0o.这样,我们就把角的概念推广到了任意角.探究一:如果你的手表慢了20分钟,或快了1小时,你应该将分钟分别旋转多少度才能
将时间校准?—120°,360°.B1γAB2αOB3y二、象限角x 为了进一步研究角的需要,我们常在直角坐标系内讨论角,并使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么对一个任意角,角的终边可能落在哪些位置? 口答:
-50°,405°,210°, -200°
分别是第几象限的角?第四象限角第一象限角第三象限角第二象限角探究二:在直角坐标系中,给
定一个角,这个角的终边唯一
确定,若给一条射线作终边,
这个角唯一吗?1.在直角坐标系中画出-30°,330°,
-390°, 这些角有什么内在联系?-32°-390°o330°, {β︱β= -30°+ k·360°,k∈Z}归纳:与-30°角终边相同的角330°=-30°+360°-390°=-30°+(-1)×360° 一般地,所有与角α终边相同的角,
连同角α在内,可构成一个集合 S={β︱β=α+k·360°,k∈Z}三、终边相同的角 练习1:写出与30°,45°,—60°终边相同的角的集合{β︱β=45 °+ k·360°,k∈Z}{β︱β=30 °+ k·360°,k∈Z}{β︱β=-60 °+ k·360°,k∈Z}例1 写出终边在y轴的角的集合.解:在0°~360°范围内,终边在y轴上的角有两
个,即90°,270°角(图1.1-6).因此,所有与
90°角终边相同的角构成集合
S1={β|β=90°+k·360°.k∈Z}.
而所有与270°角终边相同的角构成集合
S2={β|β=270°+k·360°.k∈Z}.于是,终边在y轴上的角的集合
S=S1∪S2
={β|β=90°+2k·180°,k∈Z }
∪{β|β=90°+180°+2k·180°,k∈Z }
={β|β=90°+2k·180°,k∈Z }
∪{β|β=90°+(2k+1)180°,k∈Z }
={β|β=90°+n·180°,n∈Z }例题2. 在0o到360o范围内,找出与下列各角终边相同的角,并判断它是哪个象限的角.
(1) -120o; (2) 640o;解:⑴∵-120o=-360o+240o,
∴240o的角与-120o的角终边相同,
它是第三象限角.
⑵ ∵640o=360o+280o,
∴280o的角与640o的角终边相同,
它是第四象限角. 学生活动:
1.锐角是第几象限?第一象限角一定是锐角吗?
2.钝角是第几象限?第二象限角一定是钝角?
3.直角是第几象限?轴线角一定是直角?
锐角一定是第一象限的角,第一象限角不一定是锐角.钝角一定是第二象限的角,第二象限角不一定是钝角.直角一定是轴线角,轴线角不一定是直角.正角
负角
零角象限角
轴线角终边相同角角谢谢大家
