北师大版八年级数学上册1.1 探索勾股定理课件(2课时38张ppt)
文档属性
| 名称 | 北师大版八年级数学上册1.1 探索勾股定理课件(2课时38张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 761.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-30 09:57:02 | ||
图片预览



文档简介
课件38张PPT。第一章
勾股定理八年级数学北师版·上册1.1.1 探索勾股定理授课人:XXXX新课引入
问题思考 如图,从电线杆离地面8 m处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6 m,那么需要多长的钢索?新知探究
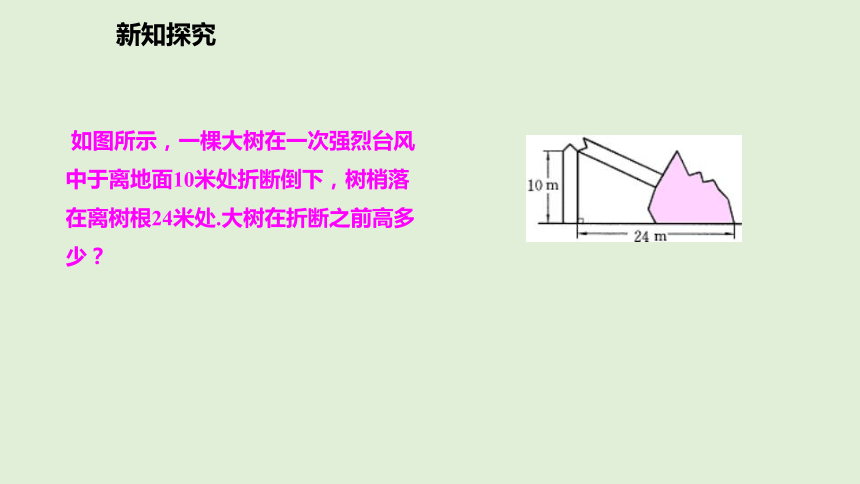
如图所示,一棵大树在一次强烈台风中于离地面10米处折断倒下,树梢落在离树根24米处.大树在折断之前高多少?
新知探究
问题:你能观察出直角三角形三边之间的关系吗?1.画一个直角三角形,使直角边长分别为3 cm和4cm,测量一下斜边长是多少?2.画一个直角边长分别是6 cm和8 cm的直角三角形,测量一下斜边长是多少?3.画一个直角边长分别是5 cm和12cm的直角三角形,测量一下斜边长是多少?5cm10cm13cm新知探究
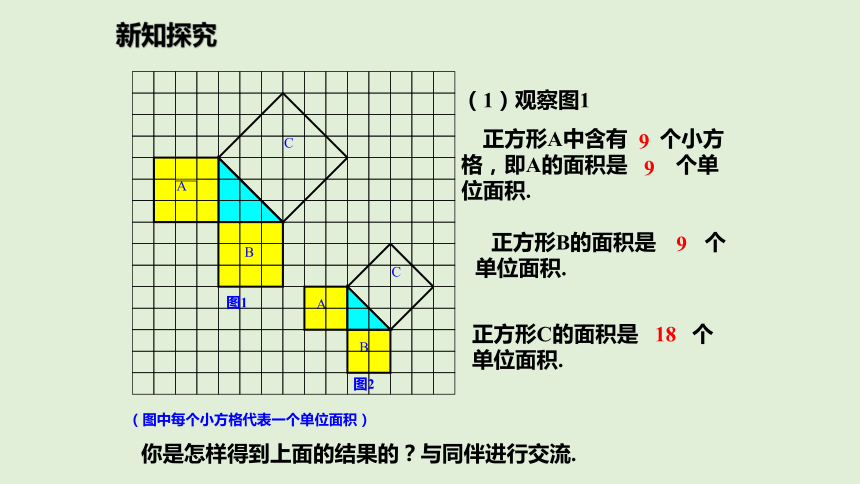
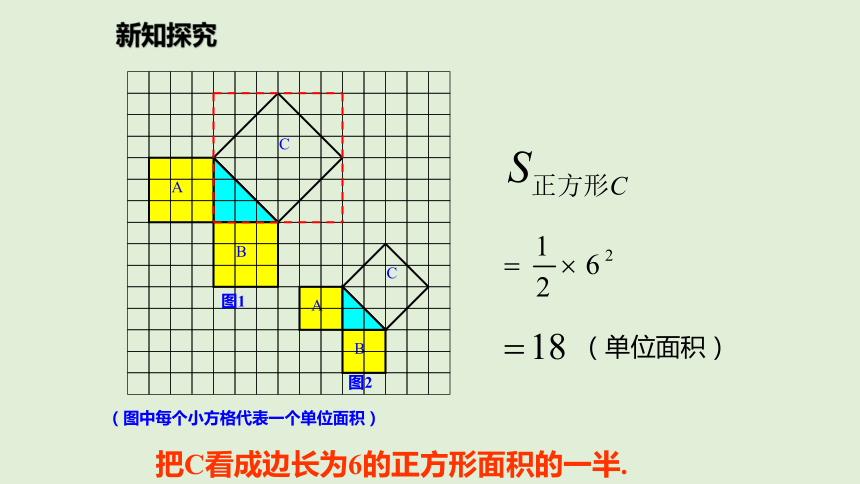
(1)观察图1
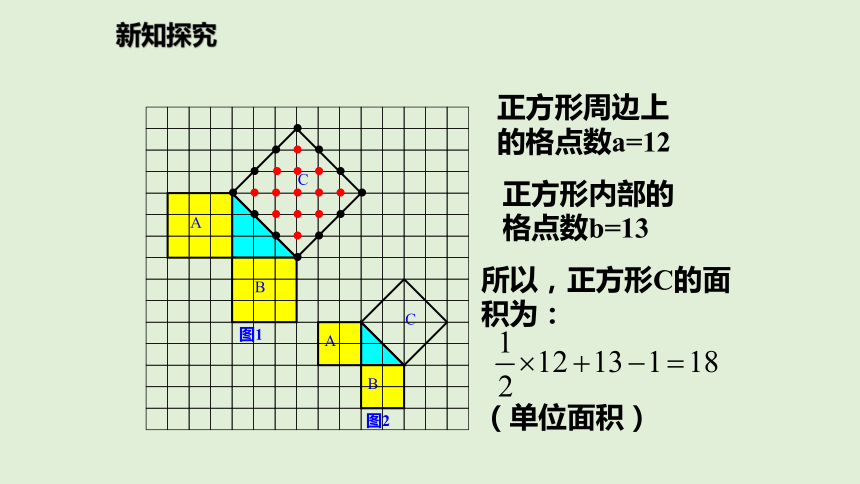
正方形A中含有 个小方格,即A的面积是 个单位面积. 正方形B的面积是 个单位面积.正方形C的面积是 个单位面积.99918你是怎样得到上面的结果的?与同伴进行交流.正方形周边上的格点数a=12正方形内部的格点数b=13所以,正方形C的面积为:
(单位面积)图1图2新知探究
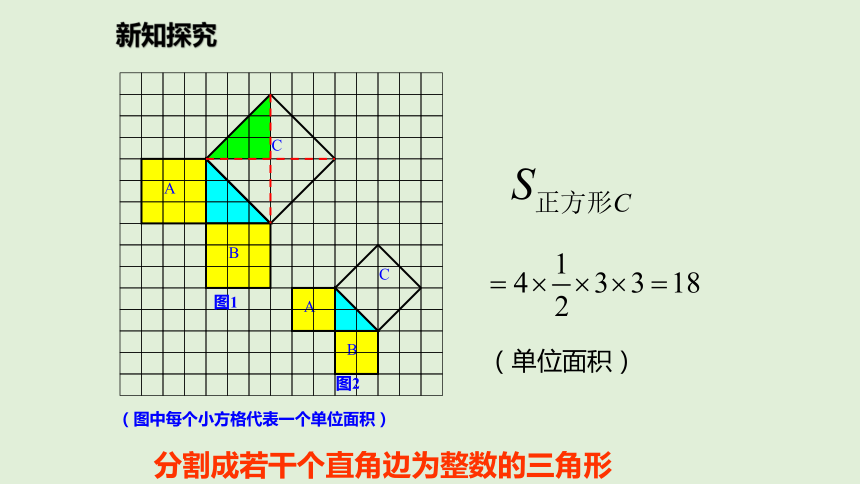
分割成若干个直角边为整数的三角形(单位面积)新知探究
(单位面积)把C看成边长为6的正方形面积的一半.新知探究
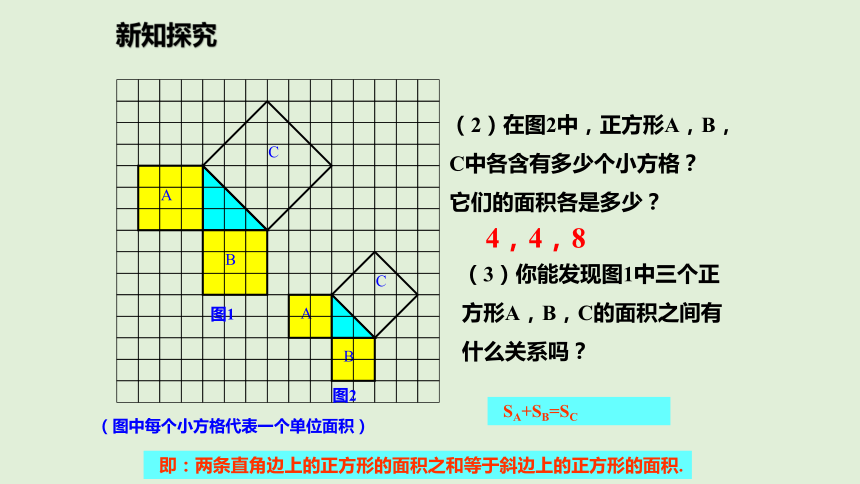
(2)在图2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?(3)你能发现图1中三个正方形A,B,C的面积之间有什么关系吗? SA+SB=SC 即:两条直角边上的正方形的面积之和等于斜边上的正方形的面积.4,4,8新知探究
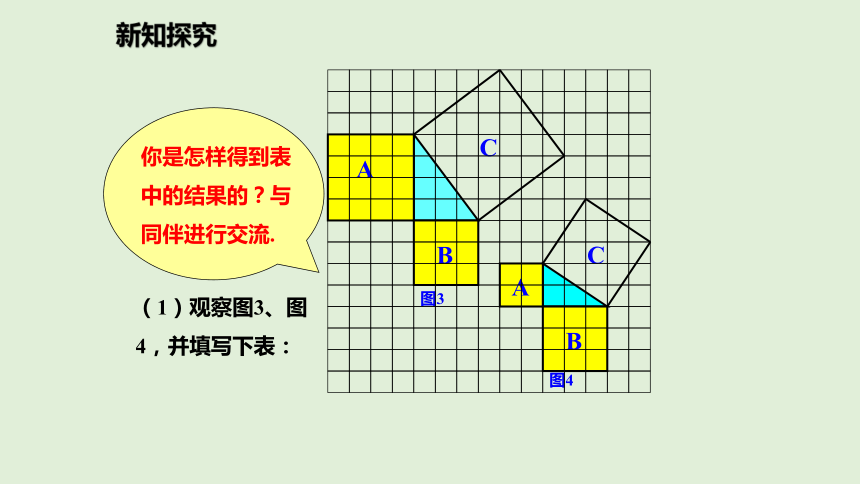
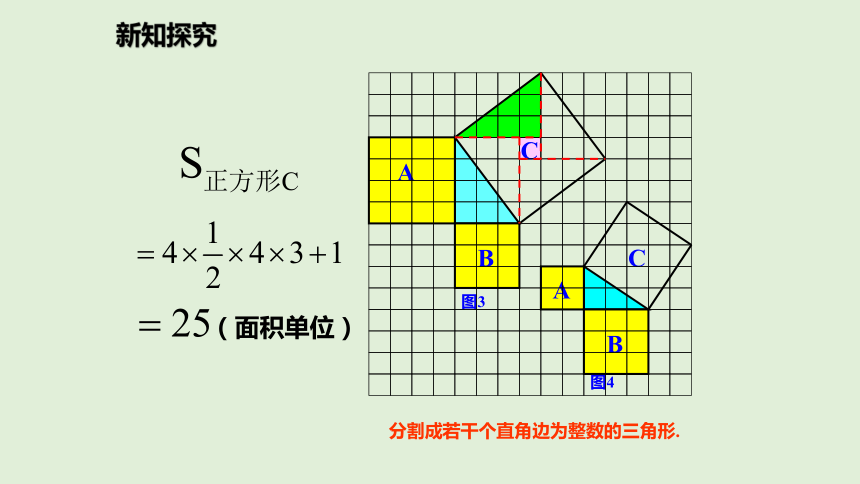
(1)观察图3、图4,并填写下表:新知探究
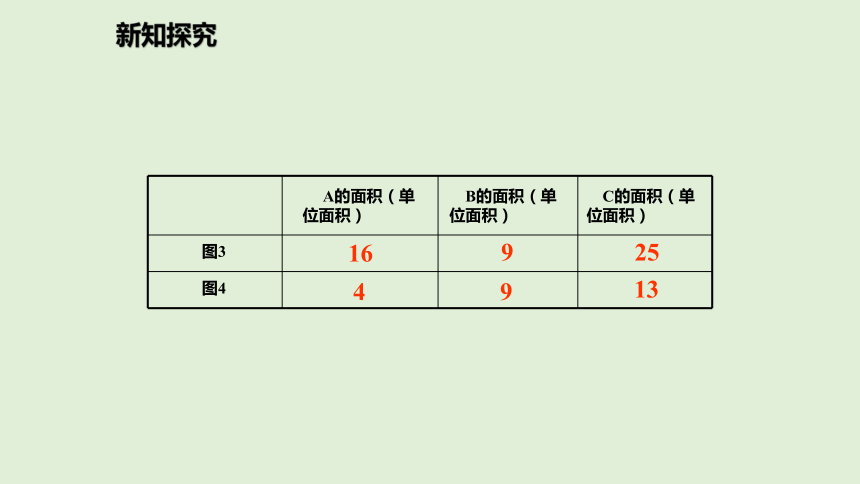
A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)图3图4169254913新知探究
分割成若干个直角边为整数的三角形.(面积单位)新知探究
(2)三个正方形A,B,C的面积之间有什么关系?SA+SB=SC
即:两条直角边上的正方形的面积之和等于斜边上的正方形的面积.新知探究
(1)你能用三角形的边长表示正方形的面积吗?(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流.(3)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度.(2)中的规律对这个三角形仍然成立吗?新知探究
勾股定理(gou-gu theorem)如果直角三角形两直角边分别为a,b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方.勾股弦新知探究
如图,从电线杆离地面8 m处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6 m,那么需要多长的钢索?解:设钢索的长度为am,
由勾股定理,得a2=82+62
∴a=10.
需要10m长的钢索.新知探究
新知探究
如图所示,一棵大树在一次强烈台风中于离地面10米处折断倒下,树梢落在离树根24米处.大树在折断之前高多少?
解:设大树折断部分长度为am,
由勾股定理,得a2=102+242
∴a=26
10+26=36m.
答:大树在折断之前高36m.1.直角三角形ABC的两直角边BC=12,AC=16,则△ABC的斜边AB的长是 ( )
A.20 B.10 C.9.6 D.8
解析:BC2=122=144,AC2=162=256,AB2=AC2+BC2=400=202.A巩固练习解析:利用勾股定理求出斜边的长为10.2.直角三角形两直角边长分别是6和8,则周长与最短边长的比是 ( )
A.7∶1 B.4∶1 C.25∶7 D.31∶7B巩固练习课堂小结勾股定理 如果直角三角形两直角边分别为a, b,斜边为c,那么直角三角形两直角边的平方和等于
斜边的平方.ac勾弦b股课堂小测解析:根据等腰三角形三线合一,判断出△ADC为直角三角形,利用勾股定理即可求出AC的长为13.1.如图所示,在△ABC中,AB=AC,AD是△ABC的角平分线,若BC=10,AD=12,则AC= .?132. 如图所示,在Rt△ABC中,∠ACB=90°,AB=10,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于 .?解析:根据半圆面积公式结合勾股定理,知S1+S2等于以斜边为直径的半圆的面积.所以S1+S2= πAB2=12.5π.12.5π课堂小测第一章 勾股定理八年级数学北师版·上册1.1.2 勾股定理的验证及计算授课人:XXXX新课引入
问题思考 分别以直角三角形的三条边为边长向外作正方形,你能利用这个图说明勾股定理的正确性吗?你是如何做的?与同伴进行交流.新知探究
∵ c2= 4? ab +(b-a)2 =2ab+b2-2ab+a2 =a2+b2∴a2+b2=c2方法一
大正方形的面积可以表示为 .
也可表示为4? ab +(b-a)2 .
c2新知探究
∵ (a+b)2 = c2 + 2aba2+2ab+b2 = c2 +2ab∴a2+b2=c2方法二
大正方形的面积可以表示为 ;
也可以表示为c2 + 2ab.
(a+b)2∴ a2 + b2 = c2c2abca2b2 方法三新知探究
abc∴ c2 = b2 + a2 方法四新知探究
aabbcc方法五∴ c2 = b2 + a2新知探究
例题我方侦察员小王在距离东西向公路400 m处侦察,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400 m,10 s后,汽车与他相距500 m,你能帮小王计算敌方汽车的速度吗? 解析: 根据题意,可以画出右图,其中点A表示小王所在位置,点C,点B表示两个时刻敌方汽车的位置.由于小王距离公路400 m,因此∠C是直角,这样就可以由勾股定理来解决这个问题了.新知探究
解:由勾股定理,可以得到AB2=BC2+AC2,也就是5002=BC2+4002,所以BC=300. 敌方汽车10 s行驶了300 m,那么它1 h行驶的距离为300×6×60=108000(m),即它行驶的速度为108 km/h.新知探究
1.下列选项中,不能用来证明勾股定理的是( ) 解析:A,B,C都可以利用图形的面积得出a,b,c的关系,即可证明勾股定理,故A,B,C选项不符合题意;D,不能利用图形的面积证明勾股定理,故此选项正确.D巩固练习2.用四个边长均为a,b,c的直角三角板,拼成如图所示的图形,则下列结论中正确的是( ) A.c2=a2+b2 B.c2=a2+2ab+b2 C.c2=a2-2ab+b2 D.c2=(a+b)2解析:由题意得到四个完全一样的直角三角板围成的四边形为正方形,其边长为c,里面的小四边形也为正方形,边长为b-a,则有c2=ab×2+(b-a)2,整理得c2=a2+b2.A巩固练习验证勾股定理的基本图形:课堂小结c2abca2b2课堂小结 abcabbcc课堂小结1.如图所示,大正方形的面积是 , 另一种方法计算大正方形的面积是 ,两种结果相等,推得勾股定理是 .?(a+b)24× ab+c2a2+b2=c2解析:如图所示,大正方形的面积是(a+b)2,另一种计算方法是4× ab+c2,即(a+b)2=4× ab+c2,化简得a2+b2=c2.
课堂小测2.操作:剪若干个大小形状完全相同的直角三角形,三边长分别记为a,b,c.如图(1)所示,分别用4张这样的直角三角形纸片拼成如图(2)(3)所示的形状,图(2)中的两个小正方形的面积S2,S3与图(3)中小正方形的面积S1有什么关系?你能得到a,b,c之间有什么关系?解:分别用4张直角三角形纸片,拼成如图(2)(3)所示的形状,观察图(2)(3)可发现,图(2)中的两个小正方形的面积之和等于图(3)中的小正方形的面积,即S2+S3=S1,这个结论用关系式可表示为a2+b2=c2.课堂小测
问题思考 如图,从电线杆离地面8 m处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6 m,那么需要多长的钢索?新知探究
如图所示,一棵大树在一次强烈台风中于离地面10米处折断倒下,树梢落在离树根24米处.大树在折断之前高多少?
新知探究
问题:你能观察出直角三角形三边之间的关系吗?1.画一个直角三角形,使直角边长分别为3 cm和4cm,测量一下斜边长是多少?2.画一个直角边长分别是6 cm和8 cm的直角三角形,测量一下斜边长是多少?3.画一个直角边长分别是5 cm和12cm的直角三角形,测量一下斜边长是多少?5cm10cm13cm新知探究
(1)观察图1
正方形A中含有 个小方格,即A的面积是 个单位面积. 正方形B的面积是 个单位面积.正方形C的面积是 个单位面积.99918你是怎样得到上面的结果的?与同伴进行交流.正方形周边上的格点数a=12正方形内部的格点数b=13所以,正方形C的面积为:
(单位面积)图1图2新知探究
分割成若干个直角边为整数的三角形(单位面积)新知探究
(单位面积)把C看成边长为6的正方形面积的一半.新知探究
(2)在图2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?(3)你能发现图1中三个正方形A,B,C的面积之间有什么关系吗? SA+SB=SC 即:两条直角边上的正方形的面积之和等于斜边上的正方形的面积.4,4,8新知探究
(1)观察图3、图4,并填写下表:新知探究
A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)图3图4169254913新知探究
分割成若干个直角边为整数的三角形.(面积单位)新知探究
(2)三个正方形A,B,C的面积之间有什么关系?SA+SB=SC
即:两条直角边上的正方形的面积之和等于斜边上的正方形的面积.新知探究
(1)你能用三角形的边长表示正方形的面积吗?(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流.(3)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度.(2)中的规律对这个三角形仍然成立吗?新知探究
勾股定理(gou-gu theorem)如果直角三角形两直角边分别为a,b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方.勾股弦新知探究
如图,从电线杆离地面8 m处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6 m,那么需要多长的钢索?解:设钢索的长度为am,
由勾股定理,得a2=82+62
∴a=10.
需要10m长的钢索.新知探究
新知探究
如图所示,一棵大树在一次强烈台风中于离地面10米处折断倒下,树梢落在离树根24米处.大树在折断之前高多少?
解:设大树折断部分长度为am,
由勾股定理,得a2=102+242
∴a=26
10+26=36m.
答:大树在折断之前高36m.1.直角三角形ABC的两直角边BC=12,AC=16,则△ABC的斜边AB的长是 ( )
A.20 B.10 C.9.6 D.8
解析:BC2=122=144,AC2=162=256,AB2=AC2+BC2=400=202.A巩固练习解析:利用勾股定理求出斜边的长为10.2.直角三角形两直角边长分别是6和8,则周长与最短边长的比是 ( )
A.7∶1 B.4∶1 C.25∶7 D.31∶7B巩固练习课堂小结勾股定理 如果直角三角形两直角边分别为a, b,斜边为c,那么直角三角形两直角边的平方和等于
斜边的平方.ac勾弦b股课堂小测解析:根据等腰三角形三线合一,判断出△ADC为直角三角形,利用勾股定理即可求出AC的长为13.1.如图所示,在△ABC中,AB=AC,AD是△ABC的角平分线,若BC=10,AD=12,则AC= .?132. 如图所示,在Rt△ABC中,∠ACB=90°,AB=10,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于 .?解析:根据半圆面积公式结合勾股定理,知S1+S2等于以斜边为直径的半圆的面积.所以S1+S2= πAB2=12.5π.12.5π课堂小测第一章 勾股定理八年级数学北师版·上册1.1.2 勾股定理的验证及计算授课人:XXXX新课引入
问题思考 分别以直角三角形的三条边为边长向外作正方形,你能利用这个图说明勾股定理的正确性吗?你是如何做的?与同伴进行交流.新知探究
∵ c2= 4? ab +(b-a)2 =2ab+b2-2ab+a2 =a2+b2∴a2+b2=c2方法一
大正方形的面积可以表示为 .
也可表示为4? ab +(b-a)2 .
c2新知探究
∵ (a+b)2 = c2 + 2aba2+2ab+b2 = c2 +2ab∴a2+b2=c2方法二
大正方形的面积可以表示为 ;
也可以表示为c2 + 2ab.
(a+b)2∴ a2 + b2 = c2c2abca2b2 方法三新知探究
abc∴ c2 = b2 + a2 方法四新知探究
aabbcc方法五∴ c2 = b2 + a2新知探究
例题我方侦察员小王在距离东西向公路400 m处侦察,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400 m,10 s后,汽车与他相距500 m,你能帮小王计算敌方汽车的速度吗? 解析: 根据题意,可以画出右图,其中点A表示小王所在位置,点C,点B表示两个时刻敌方汽车的位置.由于小王距离公路400 m,因此∠C是直角,这样就可以由勾股定理来解决这个问题了.新知探究
解:由勾股定理,可以得到AB2=BC2+AC2,也就是5002=BC2+4002,所以BC=300. 敌方汽车10 s行驶了300 m,那么它1 h行驶的距离为300×6×60=108000(m),即它行驶的速度为108 km/h.新知探究
1.下列选项中,不能用来证明勾股定理的是( ) 解析:A,B,C都可以利用图形的面积得出a,b,c的关系,即可证明勾股定理,故A,B,C选项不符合题意;D,不能利用图形的面积证明勾股定理,故此选项正确.D巩固练习2.用四个边长均为a,b,c的直角三角板,拼成如图所示的图形,则下列结论中正确的是( ) A.c2=a2+b2 B.c2=a2+2ab+b2 C.c2=a2-2ab+b2 D.c2=(a+b)2解析:由题意得到四个完全一样的直角三角板围成的四边形为正方形,其边长为c,里面的小四边形也为正方形,边长为b-a,则有c2=ab×2+(b-a)2,整理得c2=a2+b2.A巩固练习验证勾股定理的基本图形:课堂小结c2abca2b2课堂小结 abcabbcc课堂小结1.如图所示,大正方形的面积是 , 另一种方法计算大正方形的面积是 ,两种结果相等,推得勾股定理是 .?(a+b)24× ab+c2a2+b2=c2解析:如图所示,大正方形的面积是(a+b)2,另一种计算方法是4× ab+c2,即(a+b)2=4× ab+c2,化简得a2+b2=c2.
课堂小测2.操作:剪若干个大小形状完全相同的直角三角形,三边长分别记为a,b,c.如图(1)所示,分别用4张这样的直角三角形纸片拼成如图(2)(3)所示的形状,图(2)中的两个小正方形的面积S2,S3与图(3)中小正方形的面积S1有什么关系?你能得到a,b,c之间有什么关系?解:分别用4张直角三角形纸片,拼成如图(2)(3)所示的形状,观察图(2)(3)可发现,图(2)中的两个小正方形的面积之和等于图(3)中的小正方形的面积,即S2+S3=S1,这个结论用关系式可表示为a2+b2=c2.课堂小测
同课章节目录
