人教版九年级数学上册21.1 一元二次方程课件(共33张PPT)
文档属性
| 名称 | 人教版九年级数学上册21.1 一元二次方程课件(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-29 15:36:27 | ||
图片预览











文档简介
课件33张PPT。1激情引入2激情引入3激情引入 在设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加视觉美感。按此比例,如果雕像的高为2 m,
那么它的下部应设计为多高?ACBx2-xCBA2cm如图,雕像的上部高度AC与下部高度BC应有如下关系:
AC: BC=BC:2,即 BC2=2AC.
设雕像下部高xm,可得4激情引入设雕像下部高xm,可得方程x2=2(2-x),整理得
x2+2x﹣4=0. ①
这个方程与我们学过的一元一次方程不同,其中未知数x的最高次数是2.
如何解这类方程?
如何用这类方程解决一些实际问题?
这就是本章要学习的主要内容.5人教版九年级数学上册第二十一章 一元二次方程21.1 一元二次方程 一元二次方程的概念1.知道一元二次方程及一元二次方程的根的概念.
2.能将一元二次方程化为一般形式,正确认识二次项系数、一次项系数及常数项.重点:一元二次方程的概念及其一般形式.
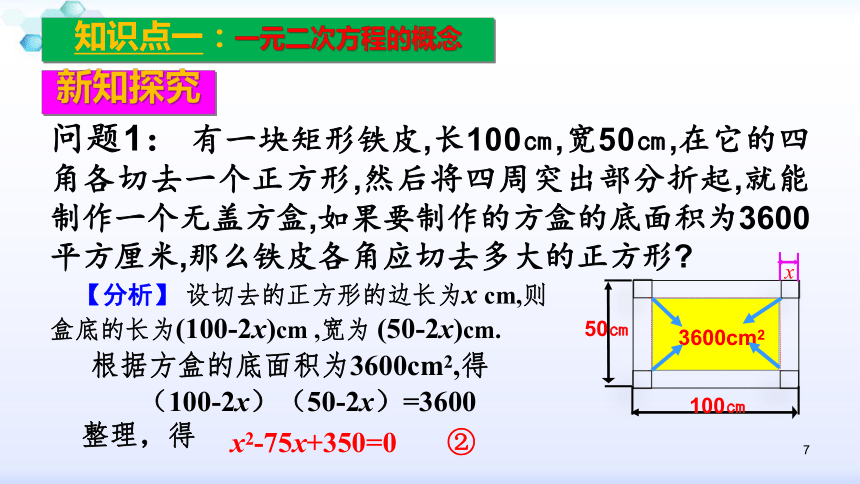
难点:正确识别一般式中的“项”及“系数”.6学习目标重点难点7新知探究知识点一:一元二次方程的概念问题1: 有一块矩形铁皮,长100㎝,宽50㎝,在它的四角各切去一个正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的方盒的底面积为3600平方厘米,那么铁皮各角应切去多大的正方形?100㎝50㎝x 【分析】 设切去的正方形的边长为x cm,则盒底的长为(100-2x)cm ,宽为 (50-2x)cm. 根据方盒的底面积为3600cm2,得整理,得(100-2x)(50-2x)=3600x2-75x+350=0 ②3600cm28新知探究知识点一:一元二次方程的概念 问题2:要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参赛? 【分析】设应邀请x个队参赛,每个队要与其他(x-1)个队各比赛一场,因为甲对乙与乙对甲是同一场比赛,所以全部比赛 x(x-1)场。
可列方程 x(x-1)=7×4
整理,得
x2-x=56 ③新知探究知识点一:一元二次方程的概念 【思考】方程①x2+2x﹣4=0
②x2-75x+350=0
③x2-x-56=0
这三个方程都不是一元一次方程.那么这三个方程与一元一次方程的区别在哪里?它们有什么共同特点呢?特点:(1)这两个方程的两边都是整式;
(2)都只含一个未知数x;
(3)它们的未知数的最高次数都是 2 次的.10归纳总结知识点一:一元二次方程的概念 像上述三个方程这样的等号两边都是整式, 只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程,叫做一元二次方程(必须满足三个特征).11学以致用知识点一:一元二次方程的概念 1 、下列方程中,一元二次方程的是( )② 3x(x-4)=0③ x2+3y=36⑤ x3+1-3x=0① ax2+ bx+c=0④⑥⑦⑧A. 1 B.2 C,3 D. 4 B先独立完成导学案互动探究1,再同桌相互交
流,最后小组交流;12合作探究知识点一:一元二次方程的概念13归纳总结 判断一个方程是否为一元二次方程, 可以从下面四个条件入手:
知识点一:一元二次方程的概念①是整式方程; ②只含一个未知数;
③含未知数的项的最高次数为2;④二次项系数不等于0.
同时满足这四个条件的方程是一元二次方程.14新知探究知识点二:一元二次方程的一般形式 一般地,任何一个关于x 的一元二次方程,经过整理,都可以化为 ax2+bx+c=0 的形式,我们把ax2+bx+c=0 (a,b,c为常数,a≠0)称为一元二次方程的一般形式. 为什么规定a≠0?15新知探究知识点二:一元二次方程的一般形式【思考】为什么要限制a≠0,b,c可以为零吗?【结论】只要满足a≠0,a,b,c可以为任意实数.当a=0时,ax2+bx+c=0
当a≠0,b=0时,ax2+bx+c=0
当a≠0,c=0时,ax2+bx+c=0
当a≠0,b=0,c=0时,ax2+bx+c=0 一元二次方程bx+c=0(一元一次方程)ax2+c=0ax2+bx=0ax2=016归纳总结知识点二:一元二次方程的一般形式ax2+c=0(a≠0),ax2+bx=0(a≠0),ax2=0(a≠0)二次项:ax2,二次项系数:a一次项:bx,一次项系数:b常数项:c17典例讲评知识点二:一元二次方程的一般形式 例1 a为何值时,下列方程为一元二次方程?(1)ax2-x=3x2(2) (a﹣1)x |a|+1 ﹣2x﹣7=0. 解:(1)将方程转化为一般形式,得
(a-3)x2-x=0,当a-3≠0,即a≠3时,原方程是一元二次方程;18知识点二:一元二次方程的一般形式 例2 将方程 3x(x-1)=5(x+2)化成一元二次方程的一般形式,并写出其中的二次项系数、一次项系数和常数项. 解: 去括号,得
3x2-3x=5x+10
整理,得
3x2-8x-10=0 二次项、二次项系数、一次项、一次项系数、常数项都是包括符号的 典例讲评 其中二次项系数是3,一次项系数是-8,常数项是-10.19学以致用知识点二:一元二次方程的一般形式 1、 方程(2a-4)x2﹣(2b﹣4)x+a=0.
(1)在什么条件下此方程为一元二次方程?
(2)在什么条件下此方程为一元一次方程? 解:(1)当 2a-4≠0,即a ≠2 时是一元二次方程. 解得:a=2 且 b ≠2 .∴当a=2 且 b ≠2 时是一元一次方程.20学以致用知识点二:一元二次方程的一般形式B3、若方程(m+2)x∣m∣﹣ 2x+7=0是关于x的一元二次方程,
则m= . 24.方程5x2=6x-8化为一般形式后,二次项系数、一次项系数、常数项分别为( )
A.5,6,-8 B.5,-6,-8 C.5,-6,8 D.6,5,-8 C21学以致用知识点二:一元二次方程的一般形式5.下列说法正确的是( )
A.方程8x2-7=0的一次项系数为﹣7
B.一元二次方程的一般形式是ax2+bx+c=0
C.当k≠0时,方程kx2+3x-1=x2为一元二次方程
D.当m取任意实数时,关于x的方程(m2+1)x2-mx-3=0都为一元二次方程
6方程(x-1)(x+3)=12化为ax2+bx+c=0的形式后,a,b,c的值分别为( )
A.1,﹣2,15 B.﹣1,2,15 C.1,2,﹣15 D.﹣1,2,﹣15DC先独立完成导学案互动探究3,再同桌相互交
流,最后小组交流;22合作探究知识点二:一元二次方程的一般形式23归纳总结 (1)一元二次方程的一般形式不是唯一的,但习惯上都把二次项的系数化为正整数.
(2)一元二次方程的二次项、二次项系数、一次项、一次项系数、常数项等都是针对一般形式而言的.
(3)指出一元二次方程各项系数时,不要漏掉前面的符号.知识点二:一元二次方程的一般形式24一元一次方程与一元二次方程有什么区别与联系?ax+b=0 (a≠0)ax2+bx+c=0 (a≠0)整式方程,只含有一个未知数未知数最高次数是1未知数最高次数是2归纳总结知识点二:一元二次方程的一般形式25新知探究知识点三:一元二次方程的根 使一元二次方程等号两边相等的未知数的值叫做一元二次方程的解,一元二次方程的解也叫做一元二次方程的根.26典例讲评知识点三:一元二次方程的根 例3 已知关于x的一元二次方程 (m-1)x2+3x-5m+4=0有一个根为2,求m. 分析: 一个根为2,即x=2,只需把x=2代入原方程. 解:依题意把x=2代入原方程,得
4(m-1)+6-5m+4=0,
整理,得
-m+6=0,
解,得 m=6.先独立完成导学案互动探究2,再同桌相互交
流,最后小组交流;27合作探究知识点三:一元二次方程的根28 1、 已知关于x的一元二次方程x2+ax+a=0的一个根是
3,求a的值.解:依题意把x=3代入原方程,得 32+3a+a=0 9+4a=0,整理,即学以致用知识点三:一元二次方程的根2.已知一元二次方程x2﹣x﹣m=0有一个根为1,则m的值为( )A.1 B.0 C.﹣1 D.2B29学以致用知识点三:一元二次方程的根 3.关于x的方程(k2-1)x2 + 2 (k-1) x + 2k + 2=0,
当k 时,是一元一次方程.当k 时,是一元二次方程.≠±1=-1 4.某公司今年4月份营业额为60万元,6月份营业额达到100万元,设该公司5、6两个月营业额的月均增长率为x,则可列方程为 .
60(x+1)2=10030学以致用知识点三:一元二次方程的根 5.已知x=1是一元二次方程x2+mx+n=0的一个根,
则m2 +2mn+n2的值为 .
6.关于x的一元二次方程x2 +bx+c=0的两个实数根为1和2,
则b= , c= .
7.在①x=2,②x= -2,③x=3,④x=-3中,是一元二次方程(x-2)2-2= 8-3x的根的是 (填序号)﹣312②、③31思维导图一元二次方程定义:一般形式:一元二次方程的根:32 对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?蓦然回首331.课本第4页练习及习题21.1;
2.《导学测评》;作业布置
那么它的下部应设计为多高?ACBx2-xCBA2cm如图,雕像的上部高度AC与下部高度BC应有如下关系:
AC: BC=BC:2,即 BC2=2AC.
设雕像下部高xm,可得4激情引入设雕像下部高xm,可得方程x2=2(2-x),整理得
x2+2x﹣4=0. ①
这个方程与我们学过的一元一次方程不同,其中未知数x的最高次数是2.
如何解这类方程?
如何用这类方程解决一些实际问题?
这就是本章要学习的主要内容.5人教版九年级数学上册第二十一章 一元二次方程21.1 一元二次方程 一元二次方程的概念1.知道一元二次方程及一元二次方程的根的概念.
2.能将一元二次方程化为一般形式,正确认识二次项系数、一次项系数及常数项.重点:一元二次方程的概念及其一般形式.
难点:正确识别一般式中的“项”及“系数”.6学习目标重点难点7新知探究知识点一:一元二次方程的概念问题1: 有一块矩形铁皮,长100㎝,宽50㎝,在它的四角各切去一个正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的方盒的底面积为3600平方厘米,那么铁皮各角应切去多大的正方形?100㎝50㎝x 【分析】 设切去的正方形的边长为x cm,则盒底的长为(100-2x)cm ,宽为 (50-2x)cm. 根据方盒的底面积为3600cm2,得整理,得(100-2x)(50-2x)=3600x2-75x+350=0 ②3600cm28新知探究知识点一:一元二次方程的概念 问题2:要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参赛? 【分析】设应邀请x个队参赛,每个队要与其他(x-1)个队各比赛一场,因为甲对乙与乙对甲是同一场比赛,所以全部比赛 x(x-1)场。
可列方程 x(x-1)=7×4
整理,得
x2-x=56 ③新知探究知识点一:一元二次方程的概念 【思考】方程①x2+2x﹣4=0
②x2-75x+350=0
③x2-x-56=0
这三个方程都不是一元一次方程.那么这三个方程与一元一次方程的区别在哪里?它们有什么共同特点呢?特点:(1)这两个方程的两边都是整式;
(2)都只含一个未知数x;
(3)它们的未知数的最高次数都是 2 次的.10归纳总结知识点一:一元二次方程的概念 像上述三个方程这样的等号两边都是整式, 只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程,叫做一元二次方程(必须满足三个特征).11学以致用知识点一:一元二次方程的概念 1 、下列方程中,一元二次方程的是( )② 3x(x-4)=0③ x2+3y=36⑤ x3+1-3x=0① ax2+ bx+c=0④⑥⑦⑧A. 1 B.2 C,3 D. 4 B先独立完成导学案互动探究1,再同桌相互交
流,最后小组交流;12合作探究知识点一:一元二次方程的概念13归纳总结 判断一个方程是否为一元二次方程, 可以从下面四个条件入手:
知识点一:一元二次方程的概念①是整式方程; ②只含一个未知数;
③含未知数的项的最高次数为2;④二次项系数不等于0.
同时满足这四个条件的方程是一元二次方程.14新知探究知识点二:一元二次方程的一般形式 一般地,任何一个关于x 的一元二次方程,经过整理,都可以化为 ax2+bx+c=0 的形式,我们把ax2+bx+c=0 (a,b,c为常数,a≠0)称为一元二次方程的一般形式. 为什么规定a≠0?15新知探究知识点二:一元二次方程的一般形式【思考】为什么要限制a≠0,b,c可以为零吗?【结论】只要满足a≠0,a,b,c可以为任意实数.当a=0时,ax2+bx+c=0
当a≠0,b=0时,ax2+bx+c=0
当a≠0,c=0时,ax2+bx+c=0
当a≠0,b=0,c=0时,ax2+bx+c=0 一元二次方程bx+c=0(一元一次方程)ax2+c=0ax2+bx=0ax2=016归纳总结知识点二:一元二次方程的一般形式ax2+c=0(a≠0),ax2+bx=0(a≠0),ax2=0(a≠0)二次项:ax2,二次项系数:a一次项:bx,一次项系数:b常数项:c17典例讲评知识点二:一元二次方程的一般形式 例1 a为何值时,下列方程为一元二次方程?(1)ax2-x=3x2(2) (a﹣1)x |a|+1 ﹣2x﹣7=0. 解:(1)将方程转化为一般形式,得
(a-3)x2-x=0,当a-3≠0,即a≠3时,原方程是一元二次方程;18知识点二:一元二次方程的一般形式 例2 将方程 3x(x-1)=5(x+2)化成一元二次方程的一般形式,并写出其中的二次项系数、一次项系数和常数项. 解: 去括号,得
3x2-3x=5x+10
整理,得
3x2-8x-10=0 二次项、二次项系数、一次项、一次项系数、常数项都是包括符号的 典例讲评 其中二次项系数是3,一次项系数是-8,常数项是-10.19学以致用知识点二:一元二次方程的一般形式 1、 方程(2a-4)x2﹣(2b﹣4)x+a=0.
(1)在什么条件下此方程为一元二次方程?
(2)在什么条件下此方程为一元一次方程? 解:(1)当 2a-4≠0,即a ≠2 时是一元二次方程. 解得:a=2 且 b ≠2 .∴当a=2 且 b ≠2 时是一元一次方程.20学以致用知识点二:一元二次方程的一般形式B3、若方程(m+2)x∣m∣﹣ 2x+7=0是关于x的一元二次方程,
则m= . 24.方程5x2=6x-8化为一般形式后,二次项系数、一次项系数、常数项分别为( )
A.5,6,-8 B.5,-6,-8 C.5,-6,8 D.6,5,-8 C21学以致用知识点二:一元二次方程的一般形式5.下列说法正确的是( )
A.方程8x2-7=0的一次项系数为﹣7
B.一元二次方程的一般形式是ax2+bx+c=0
C.当k≠0时,方程kx2+3x-1=x2为一元二次方程
D.当m取任意实数时,关于x的方程(m2+1)x2-mx-3=0都为一元二次方程
6方程(x-1)(x+3)=12化为ax2+bx+c=0的形式后,a,b,c的值分别为( )
A.1,﹣2,15 B.﹣1,2,15 C.1,2,﹣15 D.﹣1,2,﹣15DC先独立完成导学案互动探究3,再同桌相互交
流,最后小组交流;22合作探究知识点二:一元二次方程的一般形式23归纳总结 (1)一元二次方程的一般形式不是唯一的,但习惯上都把二次项的系数化为正整数.
(2)一元二次方程的二次项、二次项系数、一次项、一次项系数、常数项等都是针对一般形式而言的.
(3)指出一元二次方程各项系数时,不要漏掉前面的符号.知识点二:一元二次方程的一般形式24一元一次方程与一元二次方程有什么区别与联系?ax+b=0 (a≠0)ax2+bx+c=0 (a≠0)整式方程,只含有一个未知数未知数最高次数是1未知数最高次数是2归纳总结知识点二:一元二次方程的一般形式25新知探究知识点三:一元二次方程的根 使一元二次方程等号两边相等的未知数的值叫做一元二次方程的解,一元二次方程的解也叫做一元二次方程的根.26典例讲评知识点三:一元二次方程的根 例3 已知关于x的一元二次方程 (m-1)x2+3x-5m+4=0有一个根为2,求m. 分析: 一个根为2,即x=2,只需把x=2代入原方程. 解:依题意把x=2代入原方程,得
4(m-1)+6-5m+4=0,
整理,得
-m+6=0,
解,得 m=6.先独立完成导学案互动探究2,再同桌相互交
流,最后小组交流;27合作探究知识点三:一元二次方程的根28 1、 已知关于x的一元二次方程x2+ax+a=0的一个根是
3,求a的值.解:依题意把x=3代入原方程,得 32+3a+a=0 9+4a=0,整理,即学以致用知识点三:一元二次方程的根2.已知一元二次方程x2﹣x﹣m=0有一个根为1,则m的值为( )A.1 B.0 C.﹣1 D.2B29学以致用知识点三:一元二次方程的根 3.关于x的方程(k2-1)x2 + 2 (k-1) x + 2k + 2=0,
当k 时,是一元一次方程.当k 时,是一元二次方程.≠±1=-1 4.某公司今年4月份营业额为60万元,6月份营业额达到100万元,设该公司5、6两个月营业额的月均增长率为x,则可列方程为 .
60(x+1)2=10030学以致用知识点三:一元二次方程的根 5.已知x=1是一元二次方程x2+mx+n=0的一个根,
则m2 +2mn+n2的值为 .
6.关于x的一元二次方程x2 +bx+c=0的两个实数根为1和2,
则b= , c= .
7.在①x=2,②x= -2,③x=3,④x=-3中,是一元二次方程(x-2)2-2= 8-3x的根的是 (填序号)﹣312②、③31思维导图一元二次方程定义:一般形式:一元二次方程的根:32 对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?蓦然回首331.课本第4页练习及习题21.1;
2.《导学测评》;作业布置
同课章节目录
