五年级上册数学 2.2 图形的旋转教案 西师大版
文档属性
| 名称 | 五年级上册数学 2.2 图形的旋转教案 西师大版 |

|
|
| 格式 | zip | ||
| 文件大小 | 81.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-29 00:00:00 | ||
图片预览

文档简介
图形的旋转
/
【知识与技能】 通过观察具体实例认识旋转,探索它的基本性质.
【过程与方法】 在发现、探索的过程中完成对旋转这一图形变化从直观到抽象、从感性认识到理性认识的转变,发展学生直观想象能力,分析、归纳,抽象概括的思维能力.
【情感态度】 学生在实验探究、知识应用等数学活动中,能体验数学的具体、生动、灵活,增强数学应用意识,调动学生学习数学的主动性.
【教学重点】 归纳图形的旋转特征.
【教学难点】 旋转概念的形成过程及性质的探究过程.
/
【活动1】复习旧知,奠定基础。
1、在过去的学习中,我们曾经学习了两种几何图形的变换,它们是 平移 和 轴对称。想一想:
什么是平移?
什么是轴对称?
这两种几何变换的共同特征是什么?
2、观看课件,复习上述两个概念。
【活动2】思考探究,获取新知。
自我体验,初步感知。
观察思考,感受生活中的旋转现象。
自我探究,自学教材P59,完成下列填空:
旋转的定义: 在平面内,把一个图形绕着某一个定点转动一定的角度,这样的图形变换叫做 .这个定点叫 ,转动的角叫做 .如果图形上的点P经过旋转变为点P′,那么这两个点P和P′叫做这个旋转的 。
图形的旋转是由 和 两大因素决定的。
观察实例,熟悉概念。
达标小测评(PPT);
探究归纳旋转的性质,完成下面填空:
对应点到旋转中心的距离 ;每一对对应点与旋转中心所连线段的夹角都等于 ;旋转前、后的图形 。
【活动3】例题学习,应用新知。
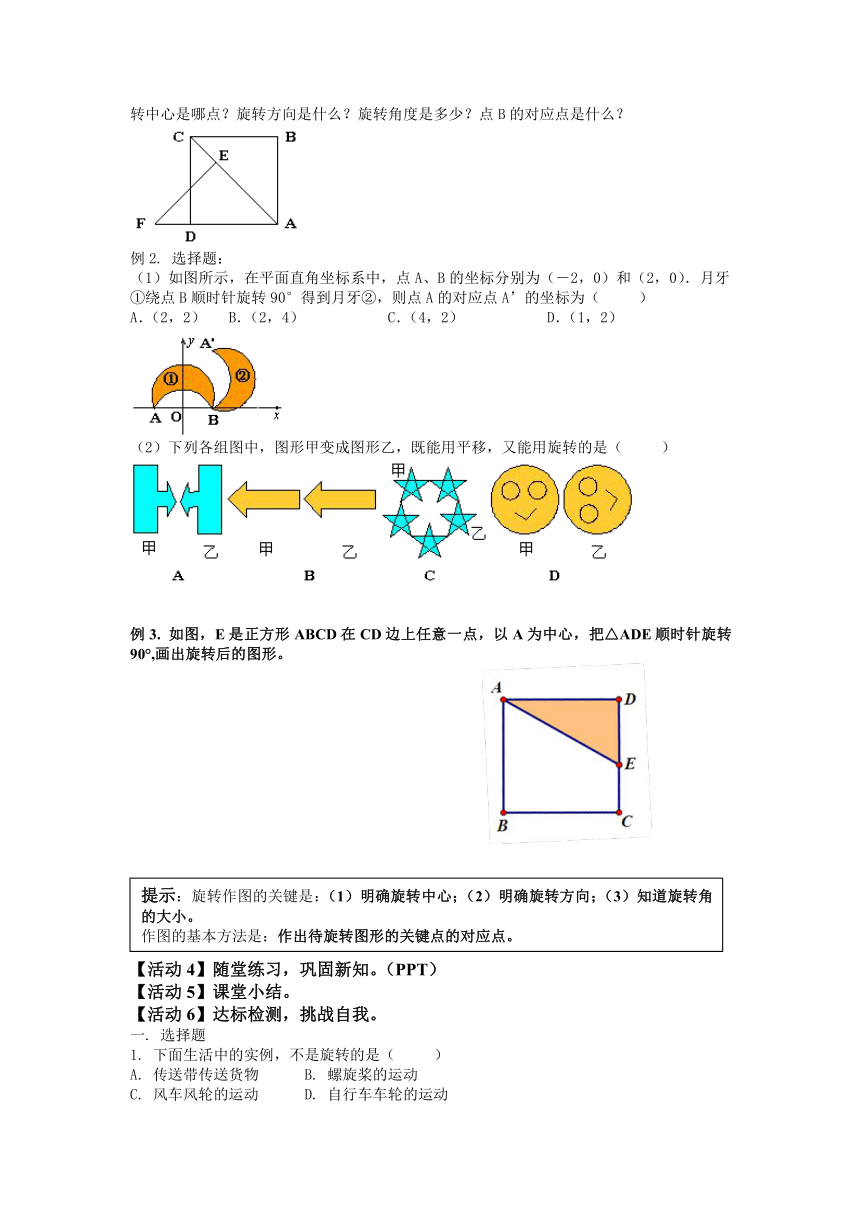
例1. 如图所示,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置,则旋转中心是哪点?旋转方向是什么?旋转角度是多少?点B的对应点是什么?
/
例2. 选择题:
(1)如图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A’的坐标为(?? )
A.(2,2)? B.(2,4)????? C.(4,2)????? D.(1,2)
/
(2)下列各组图中,图形甲变成图形乙,既能用平移,又能用旋转的是(?? )
/
例3. 如图,E是正方形ABCD在CD边上任意一点,以A为中心,把△ADE顺时针旋转90°,画出旋转后的图形。
/
【活动4】随堂练习,巩固新知。(PPT)
【活动5】课堂小结。
【活动6】达标检测,挑战自我。
一. 选择题
1. 下面生活中的实例,不是旋转的是(?? )
A. 传送带传送货物???B. 螺旋桨的运动
C. 风车风轮的运动?? D. 自行车车轮的运动
2. 中国国旗上有五个五角星,其中/四个小五角星可以看作是其中一个旋转得到的,旋转中心是(?? )
A. 最上面的小五角星/中心???? B. 最下面的小五角星中心
C. 大五角星中心???????? D. 长方形左上角的顶点
/
3. 将一个三角形旋转,旋转中心应选在(?? )
A. 三角形的顶点??????/??? B. 三角/形的外部
C. 三角形的三条边上??????? D. /平面内的任意位置
4. 如图,将△ABC绕点A逆时针/旋转80°得到△AB′C′.若∠BAC=50°,则∠CAB′/的度数为(?? )
A、30°?????B. 40°????C. 50°???/ D. 80°
/
5. 将叶片图案旋转180°后,得到的图形是(?? )
/
**6. 数学课上,老师让同学们观察如图所示的图形,问:它绕着圆心O旋转多少度后和它自身重合?/甲同学说:45°;乙同学说:60°;丙同学说:90°;丁同学说:135°.以上四位同学的回答中,错误的是(?? )
A. 甲????? B. 乙????? C. 丙????? D. 丁
/
7. 如果4张扑克按图1的形式摆放在桌面上,将其中一张旋转180°后,扑克的放置情况如图2所示,那么旋转的扑克从左起是(?? )
//
A. 第一张??????B. 第二张?????? C. 第三张????? D. 第四张
*8. 如图所示,请你先观察(1)~(3),然后确定第四张为(?? )
/
A. /??????B. /???? C./????/? D. /
二. 填空题
1. 图形的旋转是由__________和__________所决定的,旋转不改变图形的__________.
2. 由8时15分到8时40分,时钟的分针旋转的角度为__________,时针旋转的角度为__________.
3. 如图所示,其中的图(2)可以看作是由图(1)经过__________次旋转,每次旋转__________得到的.
/
三. 解答题
1. 如图所示,已知△ABC和旋转中心点O及点A的对应点D,请画出△ABC旋转后的图形△DEF.
/
2. 如图所示,某战士在训练场上练习射击,发现子弹均击中靶子上的阴影部分,你知道阴影部分的面积是多少吗? /
/
【知识与技能】 通过观察具体实例认识旋转,探索它的基本性质.
【过程与方法】 在发现、探索的过程中完成对旋转这一图形变化从直观到抽象、从感性认识到理性认识的转变,发展学生直观想象能力,分析、归纳,抽象概括的思维能力.
【情感态度】 学生在实验探究、知识应用等数学活动中,能体验数学的具体、生动、灵活,增强数学应用意识,调动学生学习数学的主动性.
【教学重点】 归纳图形的旋转特征.
【教学难点】 旋转概念的形成过程及性质的探究过程.
/
【活动1】复习旧知,奠定基础。
1、在过去的学习中,我们曾经学习了两种几何图形的变换,它们是 平移 和 轴对称。想一想:
什么是平移?
什么是轴对称?
这两种几何变换的共同特征是什么?
2、观看课件,复习上述两个概念。
【活动2】思考探究,获取新知。
自我体验,初步感知。
观察思考,感受生活中的旋转现象。
自我探究,自学教材P59,完成下列填空:
旋转的定义: 在平面内,把一个图形绕着某一个定点转动一定的角度,这样的图形变换叫做 .这个定点叫 ,转动的角叫做 .如果图形上的点P经过旋转变为点P′,那么这两个点P和P′叫做这个旋转的 。
图形的旋转是由 和 两大因素决定的。
观察实例,熟悉概念。
达标小测评(PPT);
探究归纳旋转的性质,完成下面填空:
对应点到旋转中心的距离 ;每一对对应点与旋转中心所连线段的夹角都等于 ;旋转前、后的图形 。
【活动3】例题学习,应用新知。
例1. 如图所示,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置,则旋转中心是哪点?旋转方向是什么?旋转角度是多少?点B的对应点是什么?
/
例2. 选择题:
(1)如图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A’的坐标为(?? )
A.(2,2)? B.(2,4)????? C.(4,2)????? D.(1,2)
/
(2)下列各组图中,图形甲变成图形乙,既能用平移,又能用旋转的是(?? )
/
例3. 如图,E是正方形ABCD在CD边上任意一点,以A为中心,把△ADE顺时针旋转90°,画出旋转后的图形。
/
【活动4】随堂练习,巩固新知。(PPT)
【活动5】课堂小结。
【活动6】达标检测,挑战自我。
一. 选择题
1. 下面生活中的实例,不是旋转的是(?? )
A. 传送带传送货物???B. 螺旋桨的运动
C. 风车风轮的运动?? D. 自行车车轮的运动
2. 中国国旗上有五个五角星,其中/四个小五角星可以看作是其中一个旋转得到的,旋转中心是(?? )
A. 最上面的小五角星/中心???? B. 最下面的小五角星中心
C. 大五角星中心???????? D. 长方形左上角的顶点
/
3. 将一个三角形旋转,旋转中心应选在(?? )
A. 三角形的顶点??????/??? B. 三角/形的外部
C. 三角形的三条边上??????? D. /平面内的任意位置
4. 如图,将△ABC绕点A逆时针/旋转80°得到△AB′C′.若∠BAC=50°,则∠CAB′/的度数为(?? )
A、30°?????B. 40°????C. 50°???/ D. 80°
/
5. 将叶片图案旋转180°后,得到的图形是(?? )
/
**6. 数学课上,老师让同学们观察如图所示的图形,问:它绕着圆心O旋转多少度后和它自身重合?/甲同学说:45°;乙同学说:60°;丙同学说:90°;丁同学说:135°.以上四位同学的回答中,错误的是(?? )
A. 甲????? B. 乙????? C. 丙????? D. 丁
/
7. 如果4张扑克按图1的形式摆放在桌面上,将其中一张旋转180°后,扑克的放置情况如图2所示,那么旋转的扑克从左起是(?? )
//
A. 第一张??????B. 第二张?????? C. 第三张????? D. 第四张
*8. 如图所示,请你先观察(1)~(3),然后确定第四张为(?? )
/
A. /??????B. /???? C./????/? D. /
二. 填空题
1. 图形的旋转是由__________和__________所决定的,旋转不改变图形的__________.
2. 由8时15分到8时40分,时钟的分针旋转的角度为__________,时针旋转的角度为__________.
3. 如图所示,其中的图(2)可以看作是由图(1)经过__________次旋转,每次旋转__________得到的.
/
三. 解答题
1. 如图所示,已知△ABC和旋转中心点O及点A的对应点D,请画出△ABC旋转后的图形△DEF.
/
2. 如图所示,某战士在训练场上练习射击,发现子弹均击中靶子上的阴影部分,你知道阴影部分的面积是多少吗? /
