人教版八年级数学上册 第11章 三角形--知识点复习 课件(共34张PPT)
文档属性
| 名称 | 人教版八年级数学上册 第11章 三角形--知识点复习 课件(共34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 369.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-28 20:21:24 | ||
图片预览








文档简介
课件34张PPT。1人教版八年级数学上册第十一章 三角形复 习 课 知识点复习1.知道三角形的高、中线及角平分线,多边形的边、角、对角线,正多边形等概念,会画三角形的中线高、角平分线.
2.知道三角形及多边形的外角和内角的性质,并能简单应用.
3.知道平面镶嵌的意义,能运用简单图形进行镶嵌设计..2复习目标重点:能熟练应用三角形的边、角的有关知识解决问题.
难点:应用三角形的边、角关系解决问题.3重点难点4知识链接关于三角形内角和的勒让德定理
法国数学家勒让德(A. Legendre, 1752-1833)在研究平行公理的过程中,作出了巨大贡献.
他不用欧几里得的第五公设(平行公理)证明了下列有关三角形内角和的有关定理.
勒让德第一定理:任何三角形的内角和不能大于180°.
勒让德第二定理:如果某一给定的三角形的内角和等于180°, 那么所有三角形的内角和也等于180°.
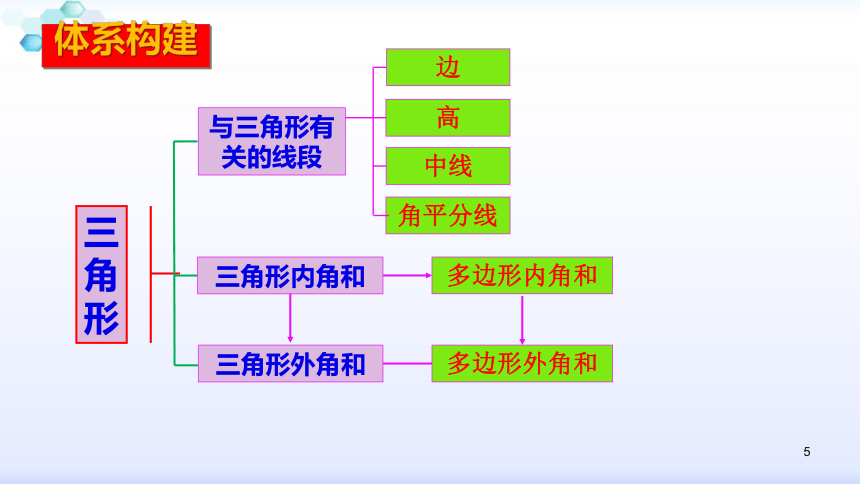
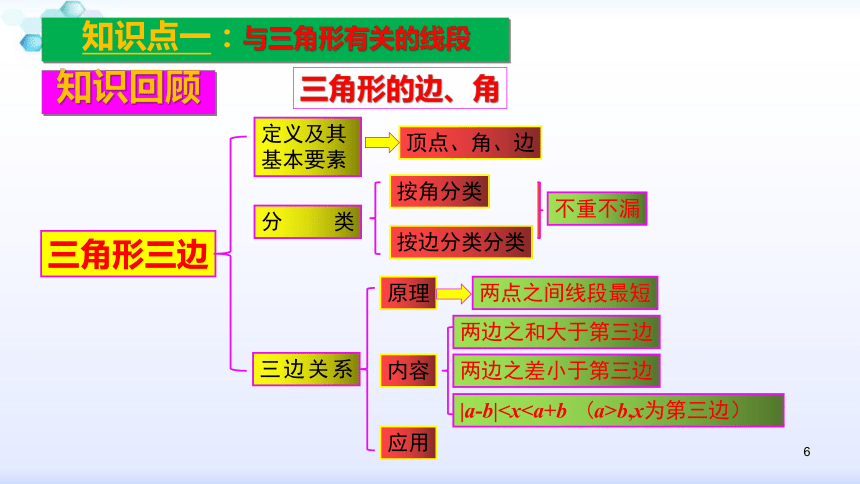
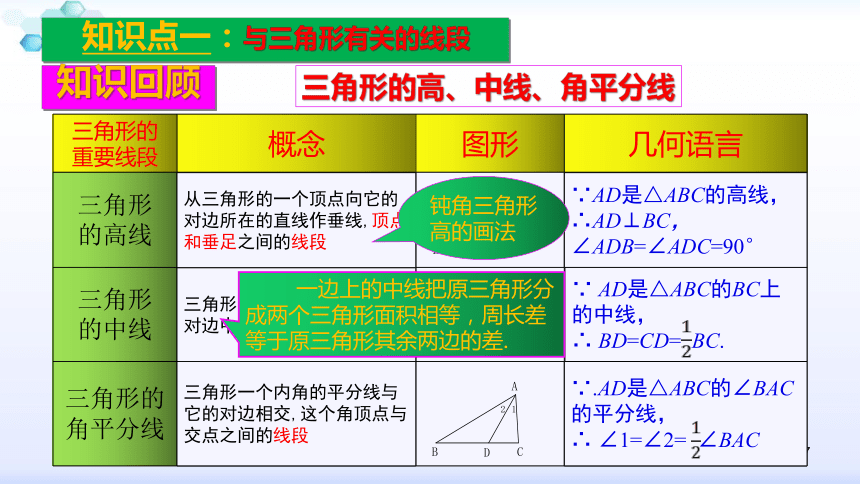
勒让德第三定理:如果某一给定的三角形的内角和小于180°, 那么所有三角形的内角和也小于180°.5体系构建三角形与三角形有关的线段三角形内角和三角形外角和边 中线 高多边形内角和多边形外角和角平分线 6知识回顾知识点一:与三角形有关的线段三角形三边定义及其基本要素顶点、角、边分类按角分类按边分类分类不重不漏三边关系原理两点之间线段最短内容两边之和大于第三边两边之差小于第三边|a-b|b,x为第三边)应用三角形的边、角7知识回顾知识点一:与三角形有关的线段∟三角形的高、中线、角平分线钝角三角形高的画法 一边上的中线把原三角形分成两个三角形面积相等,周长差等于原三角形其余两边的差.8知识回顾知识点一:与三角形有关的线段三角形的高、中线、角平分线9知识回顾知识点一:与三角形有关的线段三角形的稳定性(1)稳定性是三角形所特有的特征,在实际生产和生活中具有广泛的应用,需要保持稳定性的物体大多数都被制成三角形或包含三角形的形状,如起重机、钢架桥等.
(2)四条边及四条边以上的图形都不具有稳定性,为保证其稳定性,常在图形中构造三角形,四边形的不稳定性在实际生活中也有广泛的应用,如活动挂架、伸缩门等.10巩固练习1.如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和
△BCD的周长的差是( ).
A.2 B.3 C.6 D.不能确定
2.如果一个三角形的三条高的交点恰好是
三角形的一个顶点,那么这个三角形是( ).
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等边三角形A知识点一:与三角形有关的线段B11巩固练习知识点一:与三角形有关的线段3.在等腰三角形ABC中,AB=AC,其周长为20 cm,则AB边的取( )A.1 cm C.4 cm4.已知a,b,c是△ABC的三条边长,则化简 |a+b-c|-|c-a-b| 的结果为( )A.2a+2b-2c B.2a+2b C.2c D.0
5.王师傅用4根木条钉成一个四边形木架,要使这个木架不变形,他至少还要再钉上几根木条?( )
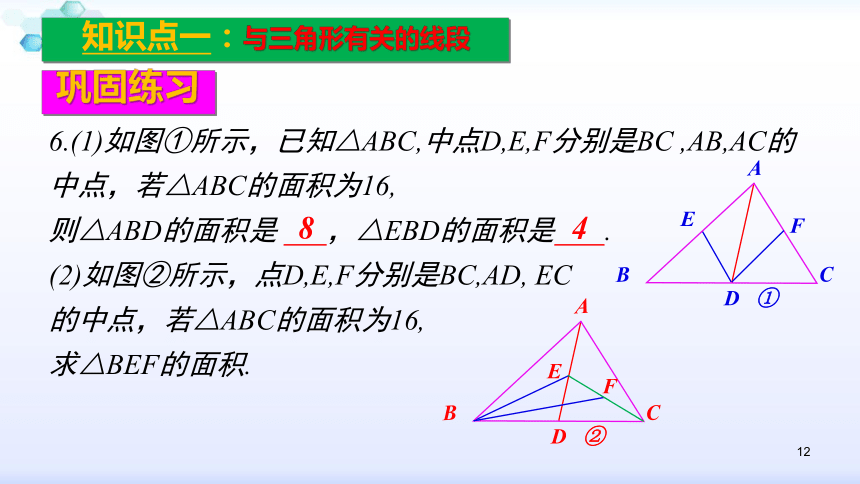
A.0根 B.1根 C.2根 D.3根BDB12巩固练习知识点一:与三角形有关的线段6.(1)如图①所示,已知△ABC,中点D,E,F分别是BC ,AB,AC的中点,若△ABC的面积为16,
则△ABD的面积是 ,△EBD的面积是 .
(2)如图②所示,点D,E,F分别是BC,AD, EC
的中点,若△ABC的面积为16,
求△BEF的面积.8413方法总结知识点一:与三角形有关的线段 解答与三角形面积有关的问题的方法:
(1)三角形一边上的中线将三角形分成面积相等的两个三角形;
(2)等底等高的三角形的面积相等;
(3) 等高的三角形的面积比等于对应底边的比.14巩固练习知识点一:与三角形有关的线段6.等腰三角形一腰上的中线把这个三角形的周长分成 12 cm
和21 cm两部分,则这个等腰三角形底边的长为( )
A.17 cm B.5cm C.5cm或17 cm D.无法确定B 本题中, 因为两部分的周长没有明确,所以首先要分两种情况考虑.最后一定要注意检查是否符合三角形的三边关系.分类讨论是解题的关健.15合作探究先独立完成导学案专题1,再同桌相互交流,
最后小组交流;知识点一:与三角形有关的线段16知识回顾知识点二:三角形的内外角和三角形内角和定理17知识回顾直角三角形的性质和判定方法知识点二:三角形的内外角和18知识回顾三角形的外角知识点二:三角形的内外角和19知识回顾三角形内角与外角结合的基本图形1
21
21
2知识点二:三角形的内外角和20巩固练习1.如果三角形的一个外角和与它不相邻的两个内角的和为180°,那么这个外角等于( )A.30°B.60°C.90° D.120°
2.如图所示,在△ABC中,∠A= 52°,∠ABC与∠ACB的平分线交于点D1,∠ABD与∠ACD的平分线
交于点D2,依此类推,∠ABD4与∠ACD4
的平分线交于点D5,则∠BD5C的度数
是( ).A 56°B.60°C.68°D.94°C知识点二:三角形的内外角和A21巩固练习知识点二:三角形的内外角和3.如图所示,AE是△ABC的角平分线,
AD⊥BC于点D,若∠BAC= 128°,
∠C=36°,则∠DAE的度数是( )
A.10°B.12°C.15°D.18°
4.将一副三角尺按如图所示的方式放置,
已知AE// BC,则∠AFD的度数是( )
A.45°B.50°C.60°D.75°AD22巩固练习知识点二:三角形的内外角和5.如图所示,G是△AFE两外角平分线的交点,P是△ABC的两外角平分线的交点,F,C在AN上,B,E在AM上,如果∠FGE=66°,那么∠P= 度.
6.已知△ABC中,高BD和CE所在直线相交于点O,且△ABC不是直角三角形,∠A=53°,则∠BOC= .66127°23巩固练习知识点二:三角形的内外角和7.如图所示,在△ABC中,AD⊥BC,AE平分∠BAC,
AG⊥AE,CG是△ABC外角ACF的平分线,
若∠G﹣∠ DAE= 60°,
则∠ACB = .24归纳总结(1)三角形的内角和、角平分线与高经常综合考查.灵活运用它们的性质通过转化思想可以求线段的长和角的度.
(2)由第3、7题可得出一个重要的结论:从三角形的一个顶点作高、角平分线,它们的夹角等于另外两个角差的一半.知识点二:三角形的内外角和25合作探究先独立完成导学案专题二第5题,再同桌相互交流,
最后小组交流;知识点二:三角形的内外角和26知识回顾知识点三:多边形及其内角和 (1)n边形从一个顶点出发的对角线条数
为: 条(n≥3);
把多边形分割成 个三角形;
(2)n边形共有对角线 条(n≥3).(n-3)(n-2)27知识回顾知识点三:多边形及其内角和多边形内角和
(1)已知边数,求内角和;
(2)已知内角和,求边数;
(3)正n边形的各条边都相等,各个角都相等,其内角和为(n-2)×180°,故正n边形的每个内角都为
(n-2) ×180°
n28巩固练习1、如图所示,每个涂色部分都是以四边形
的各顶点为圆心,1为半径画弧所得,则涂
色部分的面积之和是( )
A.0.5π B.π C.2π D.无法计算
2如果把多边形的边数增加一倍,得到的新多边形的内角和是1440°,那么原来多边形的边数是( )
A.4 B.5 C.6 D.7B知识点三:多边形及其内角和B29巩固练习3、在一个多边形中,除了两个内角外,其余内角之和为2002°,则这个多边形的边数为( )
A.12 B.12或13 C.14 D.14或15
4.一个凸n边形,除去一个内角外其余的内角和是2570°,则这个多边形对角线条数为 .知识点三:多边形及其内角和D11930巩固练习5.如图所示,小华从M点出发,沿直线前进10米,然后左转20米,再沿直线前进10米后,又向左转20°……这样走下去,他第一次回到出发地M时行走了 米.知识点三:多边形及其内角和18031合作探究先独立完成导学案专题2、3,再同桌相互交流,
最后小组交流;知识点三:多边形及其内角和知识结构图32边、顶点、内角三条高交于一点,得互余关系分的两个角相等,三条角平分线交与三角形内一点三角形三个内角的和等于180°等分对边且分得两个三角形面积相等,三条中线交点叫三角形的重心直角三角形的两个锐角互余有两个角互余的三角形是直角三角形每条边都相等,每个内角都等于 ,每个外角都等于 . 内角和等于 ,外角和等于 . 两边之和大于第三边,两边只差小于第三边33 对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?蓦然回首341.课本第28页:复习11;
2.《导学测评》;作业布置
2.知道三角形及多边形的外角和内角的性质,并能简单应用.
3.知道平面镶嵌的意义,能运用简单图形进行镶嵌设计..2复习目标重点:能熟练应用三角形的边、角的有关知识解决问题.
难点:应用三角形的边、角关系解决问题.3重点难点4知识链接关于三角形内角和的勒让德定理
法国数学家勒让德(A. Legendre, 1752-1833)在研究平行公理的过程中,作出了巨大贡献.
他不用欧几里得的第五公设(平行公理)证明了下列有关三角形内角和的有关定理.
勒让德第一定理:任何三角形的内角和不能大于180°.
勒让德第二定理:如果某一给定的三角形的内角和等于180°, 那么所有三角形的内角和也等于180°.
勒让德第三定理:如果某一给定的三角形的内角和小于180°, 那么所有三角形的内角和也小于180°.5体系构建三角形与三角形有关的线段三角形内角和三角形外角和边 中线 高多边形内角和多边形外角和角平分线 6知识回顾知识点一:与三角形有关的线段三角形三边定义及其基本要素顶点、角、边分类按角分类按边分类分类不重不漏三边关系原理两点之间线段最短内容两边之和大于第三边两边之差小于第三边|a-b|
(2)四条边及四条边以上的图形都不具有稳定性,为保证其稳定性,常在图形中构造三角形,四边形的不稳定性在实际生活中也有广泛的应用,如活动挂架、伸缩门等.10巩固练习1.如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和
△BCD的周长的差是( ).
A.2 B.3 C.6 D.不能确定
2.如果一个三角形的三条高的交点恰好是
三角形的一个顶点,那么这个三角形是( ).
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等边三角形A知识点一:与三角形有关的线段B11巩固练习知识点一:与三角形有关的线段3.在等腰三角形ABC中,AB=AC,其周长为20 cm,则AB边的取( )A.1 cm
5.王师傅用4根木条钉成一个四边形木架,要使这个木架不变形,他至少还要再钉上几根木条?( )
A.0根 B.1根 C.2根 D.3根BDB12巩固练习知识点一:与三角形有关的线段6.(1)如图①所示,已知△ABC,中点D,E,F分别是BC ,AB,AC的中点,若△ABC的面积为16,
则△ABD的面积是 ,△EBD的面积是 .
(2)如图②所示,点D,E,F分别是BC,AD, EC
的中点,若△ABC的面积为16,
求△BEF的面积.8413方法总结知识点一:与三角形有关的线段 解答与三角形面积有关的问题的方法:
(1)三角形一边上的中线将三角形分成面积相等的两个三角形;
(2)等底等高的三角形的面积相等;
(3) 等高的三角形的面积比等于对应底边的比.14巩固练习知识点一:与三角形有关的线段6.等腰三角形一腰上的中线把这个三角形的周长分成 12 cm
和21 cm两部分,则这个等腰三角形底边的长为( )
A.17 cm B.5cm C.5cm或17 cm D.无法确定B 本题中, 因为两部分的周长没有明确,所以首先要分两种情况考虑.最后一定要注意检查是否符合三角形的三边关系.分类讨论是解题的关健.15合作探究先独立完成导学案专题1,再同桌相互交流,
最后小组交流;知识点一:与三角形有关的线段16知识回顾知识点二:三角形的内外角和三角形内角和定理17知识回顾直角三角形的性质和判定方法知识点二:三角形的内外角和18知识回顾三角形的外角知识点二:三角形的内外角和19知识回顾三角形内角与外角结合的基本图形1
21
21
2知识点二:三角形的内外角和20巩固练习1.如果三角形的一个外角和与它不相邻的两个内角的和为180°,那么这个外角等于( )A.30°B.60°C.90° D.120°
2.如图所示,在△ABC中,∠A= 52°,∠ABC与∠ACB的平分线交于点D1,∠ABD与∠ACD的平分线
交于点D2,依此类推,∠ABD4与∠ACD4
的平分线交于点D5,则∠BD5C的度数
是( ).A 56°B.60°C.68°D.94°C知识点二:三角形的内外角和A21巩固练习知识点二:三角形的内外角和3.如图所示,AE是△ABC的角平分线,
AD⊥BC于点D,若∠BAC= 128°,
∠C=36°,则∠DAE的度数是( )
A.10°B.12°C.15°D.18°
4.将一副三角尺按如图所示的方式放置,
已知AE// BC,则∠AFD的度数是( )
A.45°B.50°C.60°D.75°AD22巩固练习知识点二:三角形的内外角和5.如图所示,G是△AFE两外角平分线的交点,P是△ABC的两外角平分线的交点,F,C在AN上,B,E在AM上,如果∠FGE=66°,那么∠P= 度.
6.已知△ABC中,高BD和CE所在直线相交于点O,且△ABC不是直角三角形,∠A=53°,则∠BOC= .66127°23巩固练习知识点二:三角形的内外角和7.如图所示,在△ABC中,AD⊥BC,AE平分∠BAC,
AG⊥AE,CG是△ABC外角ACF的平分线,
若∠G﹣∠ DAE= 60°,
则∠ACB = .24归纳总结(1)三角形的内角和、角平分线与高经常综合考查.灵活运用它们的性质通过转化思想可以求线段的长和角的度.
(2)由第3、7题可得出一个重要的结论:从三角形的一个顶点作高、角平分线,它们的夹角等于另外两个角差的一半.知识点二:三角形的内外角和25合作探究先独立完成导学案专题二第5题,再同桌相互交流,
最后小组交流;知识点二:三角形的内外角和26知识回顾知识点三:多边形及其内角和 (1)n边形从一个顶点出发的对角线条数
为: 条(n≥3);
把多边形分割成 个三角形;
(2)n边形共有对角线 条(n≥3).(n-3)(n-2)27知识回顾知识点三:多边形及其内角和多边形内角和
(1)已知边数,求内角和;
(2)已知内角和,求边数;
(3)正n边形的各条边都相等,各个角都相等,其内角和为(n-2)×180°,故正n边形的每个内角都为
(n-2) ×180°
n28巩固练习1、如图所示,每个涂色部分都是以四边形
的各顶点为圆心,1为半径画弧所得,则涂
色部分的面积之和是( )
A.0.5π B.π C.2π D.无法计算
2如果把多边形的边数增加一倍,得到的新多边形的内角和是1440°,那么原来多边形的边数是( )
A.4 B.5 C.6 D.7B知识点三:多边形及其内角和B29巩固练习3、在一个多边形中,除了两个内角外,其余内角之和为2002°,则这个多边形的边数为( )
A.12 B.12或13 C.14 D.14或15
4.一个凸n边形,除去一个内角外其余的内角和是2570°,则这个多边形对角线条数为 .知识点三:多边形及其内角和D11930巩固练习5.如图所示,小华从M点出发,沿直线前进10米,然后左转20米,再沿直线前进10米后,又向左转20°……这样走下去,他第一次回到出发地M时行走了 米.知识点三:多边形及其内角和18031合作探究先独立完成导学案专题2、3,再同桌相互交流,
最后小组交流;知识点三:多边形及其内角和知识结构图32边、顶点、内角三条高交于一点,得互余关系分的两个角相等,三条角平分线交与三角形内一点三角形三个内角的和等于180°等分对边且分得两个三角形面积相等,三条中线交点叫三角形的重心直角三角形的两个锐角互余有两个角互余的三角形是直角三角形每条边都相等,每个内角都等于 ,每个外角都等于 . 内角和等于 ,外角和等于 . 两边之和大于第三边,两边只差小于第三边33 对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?蓦然回首341.课本第28页:复习11;
2.《导学测评》;作业布置
