【A典演练】第7课时 第一章 第三节 正方形的性质与判定(1) 习题课件
文档属性
| 名称 | 【A典演练】第7课时 第一章 第三节 正方形的性质与判定(1) 习题课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 680.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-03 00:00:00 | ||
图片预览


文档简介
课件10张PPT。 第一单元 特殊平行四边形第7课时 正方形的性质与判定(1) 北师大版 九年级上册考点 1 正方形边,角的性质
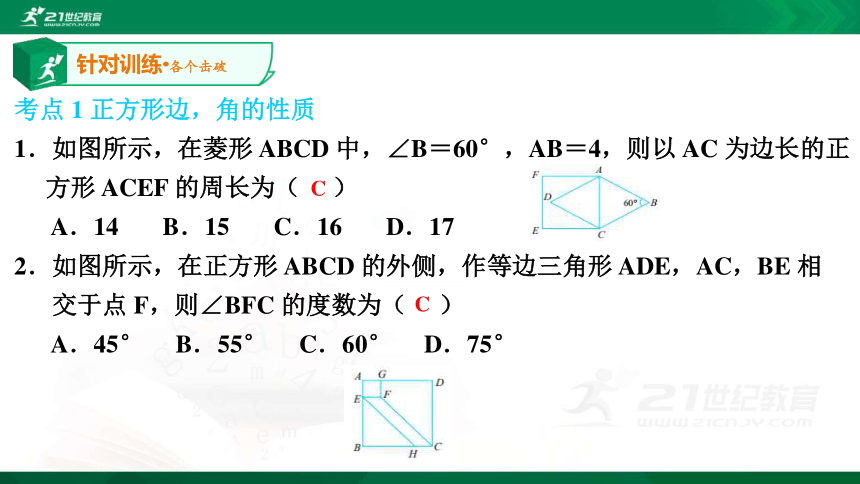
1.如图所示,在菱形 ABCD 中,∠B=60°,AB=4,则以 AC 为边长的正
方形 ACEF 的周长为( )
A.14 B.15 C.16 D.17
2.如图所示,在正方形 ABCD 的外侧,作等边三角形 ADE,AC,BE 相
交于点 F,则∠BFC 的度数为( )
A.45° B.55° C.60° D.75°
针对训练·各个击破CC考点 1 正方形边,角的性质
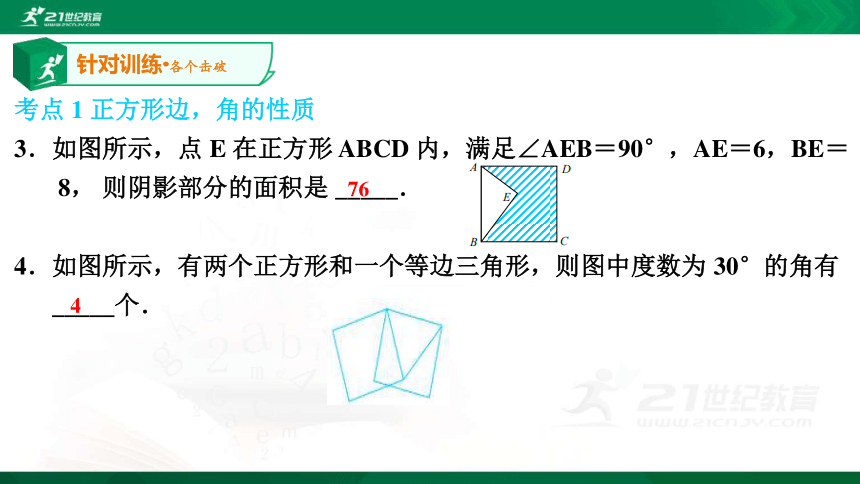
3.如图所示,点 E 在正方形 ABCD 内,满足∠AEB=90°,AE=6,BE=
8, 则阴影部分的面积是 _____.
4.如图所示,有两个正方形和一个等边三角形,则图中度数为 30°的角有
_____个.
针对训练·各个击破764考点 2 正方形对角线的性质
5.如图所示,在正方形 ABCD 中,对角线 AC,BD 相交于点 O,则图中的
等腰三角形有( )
A.4 个 B.6 个 C.8 个 D.10 个
6.如图所示,在正方形 ABCD 中,E 为正方形对角线 BD 上一点,BE=BC
,则∠BEC 的度数为( )
A.45° B.60° C.67.5° D.82.5°
针对训练·各个击破CC考点 2 正方形对角线的性质
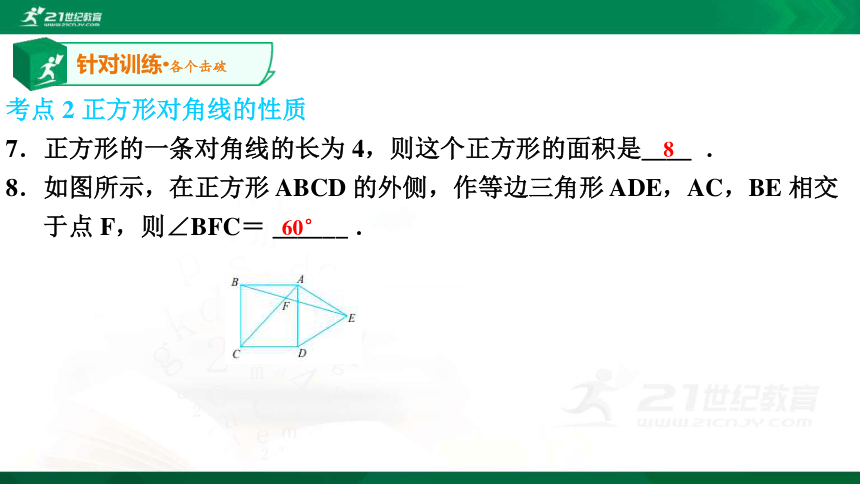
7.正方形的一条对角线的长为 4,则这个正方形的面积是____ .
8.如图所示,在正方形 ABCD 的外侧,作等边三角形 ADE,AC,BE 相交
于点 F,则∠BFC= ______ .针对训练·各个击破860°9. 如图所示,在正方形 ABCD 中,E 为对角线 AC 上一点,连接 EB,ED
(1)求证:△BEC≌△DEC;
【答案】(1)∵四边形 ABCD 是正方形,
∴CD=CB.
又∵AC 是正方形的对角线,
∴∠DCA=∠BCA. 又 CE=CE,
∴△BEC≌△DEC(SAS)
巩固提升·融会贯通9. 如图所示,在正方形 ABCD 中,E 为对角线 AC 上一点,连接 EB,ED
(2)延长 BE 交 AD 于点 F,若∠DEB=140°,求∠AFE 的度数.
【答案】(2)∵∠DEB=140°,由△BEC≌△DEC,
可得∠DEC=∠BEC=140÷2=70°,
∴∠AEF=∠BEC=70°, 又 AC 是正方形的对角线,
∠DAB=90°,
∴∠DAC=∠BAC=90°÷2=45°,
在△AEF 中,∠AFE=180°-70°-45°=65°.
巩固提升·融会贯通10.如图所示,在正方形 ABCD 中,点 E(与点 B,C 不重合)是 BC 边上
一点,将线段 EA 绕点 E 顺时针旋转 90°到 EF,过点 F 作 BC 的垂线
交BC 的延长线于点 G,连接 CF.
(1)求证:△ABE≌△EGF;
【答案】(1)∵EF⊥AE,∴∠AEB+∠GEF=90°,
又∵∠AEB+∠BAE=90°,∴∠GEF=∠BAE,
又∵FG⊥BC,∴∠ABE=∠EGF=90°.
在△ABE 与△EGF 中,
∴△ABE≌△EGF(AAS);
巩固提升·融会贯通10.如图所示,在正方形 ABCD 中,点 E(与点 B,C 不重合)是 BC 边上
一点,将线段 EA 绕点 E 顺时针旋转 90°到 EF,过点 F 作 BC 的垂线
交BC 的延长线于点 G,连接 CF.
(2)若 AB=2,S△ABE=2S△ECF,求 BE.
【答案】(2)∵△ABE≌△EGF,AB=2,
∴AB=EG=2,S△ABE=S△EGF.
∵S△ABE=2S△ECF, ∴S△EGF=2S△ECF.
∴EC=CG=1.∵四边形 ABCD 是正方形,
∴BC=AB=2, ∴BE=2-1=1.巩固提升·融会贯通谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1.如图所示,在菱形 ABCD 中,∠B=60°,AB=4,则以 AC 为边长的正
方形 ACEF 的周长为( )
A.14 B.15 C.16 D.17
2.如图所示,在正方形 ABCD 的外侧,作等边三角形 ADE,AC,BE 相
交于点 F,则∠BFC 的度数为( )
A.45° B.55° C.60° D.75°
针对训练·各个击破CC考点 1 正方形边,角的性质
3.如图所示,点 E 在正方形 ABCD 内,满足∠AEB=90°,AE=6,BE=
8, 则阴影部分的面积是 _____.
4.如图所示,有两个正方形和一个等边三角形,则图中度数为 30°的角有
_____个.
针对训练·各个击破764考点 2 正方形对角线的性质
5.如图所示,在正方形 ABCD 中,对角线 AC,BD 相交于点 O,则图中的
等腰三角形有( )
A.4 个 B.6 个 C.8 个 D.10 个
6.如图所示,在正方形 ABCD 中,E 为正方形对角线 BD 上一点,BE=BC
,则∠BEC 的度数为( )
A.45° B.60° C.67.5° D.82.5°
针对训练·各个击破CC考点 2 正方形对角线的性质
7.正方形的一条对角线的长为 4,则这个正方形的面积是____ .
8.如图所示,在正方形 ABCD 的外侧,作等边三角形 ADE,AC,BE 相交
于点 F,则∠BFC= ______ .针对训练·各个击破860°9. 如图所示,在正方形 ABCD 中,E 为对角线 AC 上一点,连接 EB,ED
(1)求证:△BEC≌△DEC;
【答案】(1)∵四边形 ABCD 是正方形,
∴CD=CB.
又∵AC 是正方形的对角线,
∴∠DCA=∠BCA. 又 CE=CE,
∴△BEC≌△DEC(SAS)
巩固提升·融会贯通9. 如图所示,在正方形 ABCD 中,E 为对角线 AC 上一点,连接 EB,ED
(2)延长 BE 交 AD 于点 F,若∠DEB=140°,求∠AFE 的度数.
【答案】(2)∵∠DEB=140°,由△BEC≌△DEC,
可得∠DEC=∠BEC=140÷2=70°,
∴∠AEF=∠BEC=70°, 又 AC 是正方形的对角线,
∠DAB=90°,
∴∠DAC=∠BAC=90°÷2=45°,
在△AEF 中,∠AFE=180°-70°-45°=65°.
巩固提升·融会贯通10.如图所示,在正方形 ABCD 中,点 E(与点 B,C 不重合)是 BC 边上
一点,将线段 EA 绕点 E 顺时针旋转 90°到 EF,过点 F 作 BC 的垂线
交BC 的延长线于点 G,连接 CF.
(1)求证:△ABE≌△EGF;
【答案】(1)∵EF⊥AE,∴∠AEB+∠GEF=90°,
又∵∠AEB+∠BAE=90°,∴∠GEF=∠BAE,
又∵FG⊥BC,∴∠ABE=∠EGF=90°.
在△ABE 与△EGF 中,
∴△ABE≌△EGF(AAS);
巩固提升·融会贯通10.如图所示,在正方形 ABCD 中,点 E(与点 B,C 不重合)是 BC 边上
一点,将线段 EA 绕点 E 顺时针旋转 90°到 EF,过点 F 作 BC 的垂线
交BC 的延长线于点 G,连接 CF.
(2)若 AB=2,S△ABE=2S△ECF,求 BE.
【答案】(2)∵△ABE≌△EGF,AB=2,
∴AB=EG=2,S△ABE=S△EGF.
∵S△ABE=2S△ECF, ∴S△EGF=2S△ECF.
∴EC=CG=1.∵四边形 ABCD 是正方形,
∴BC=AB=2, ∴BE=2-1=1.巩固提升·融会贯通谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
