2.1.4 数乘向量 课件(20张PPT)
文档属性
| 名称 | 2.1.4 数乘向量 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 426.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-30 08:21:49 | ||
图片预览







文档简介
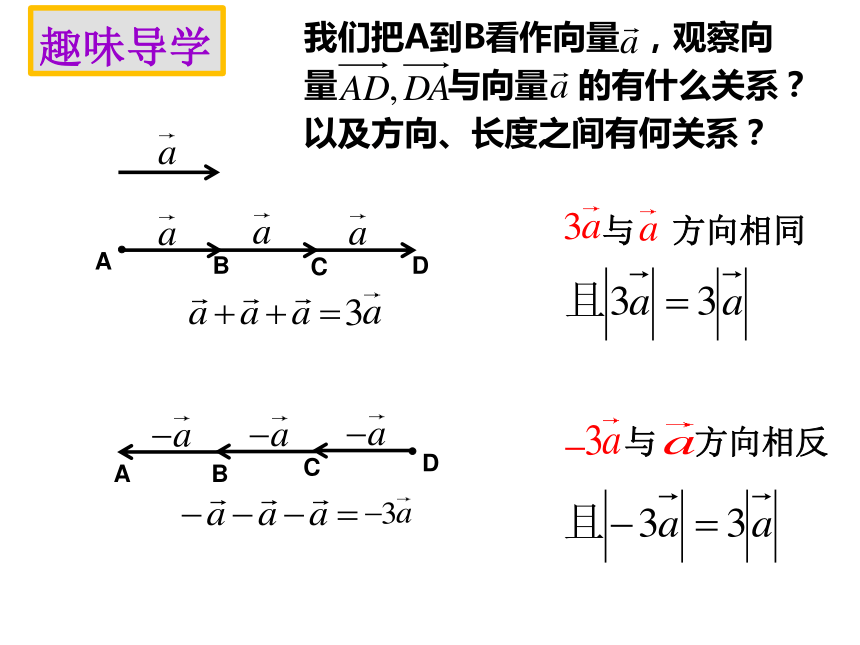
课件20张PPT。2.2.3向量数乘运算及其几何意义趣味导学 学校在一条长60米的笔直跑道上做拓展训练.从设在最北端的A点向正东方向跑20米到达B点做一道“猜谜题”,再向正东方向跑20米到达C点做一道“常识题”,又向正东方向跑20米到达终点D点做一道“脑筋急转弯题”,最后原路跑回到起点A,用时少者为优胜者.我们把A到B看作向量 ,观察向量 与向量 有什么关系?以及方向、长度之间有何关系?BCDCBA与 方向相同与 方向相反趣味导学我们把A到B看作向量 ,观察向量 与向量 的有什么关系?以及方向、长度之间有何关系? 一般地,我们规定实数λ与向量 的积是一个 ,这种运算叫做 ,记作 ,它的长度和方向规定如下:(2)当 时, 的方向与 的方向相同;
当 时, 的方向与 的方向相反;
当 时,知识点1、向量数乘运算: 新课讲授注意:①实数与向量的乘积等于一个向量;
②
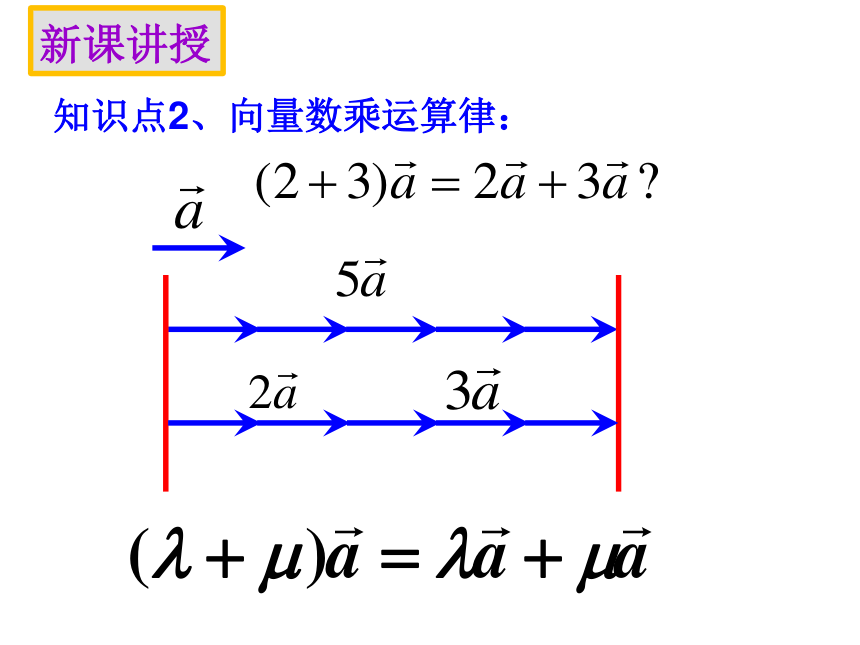
③数乘运算不等同于向量的乘法。 向量向量的数乘(1)长度:知识点2、向量数乘运算律: 新课讲授新课讲授知识点2、向量数乘运算律: 知识点2、向量数乘运算律: 新课讲授向量的加、减、数乘运算统称为向量的线性运算.新课讲授知识点2、向量数乘运算律: 特别的: 和 一般的对于任意向量 、 ,以及任意实数
, 恒有新课讲授(1)(2)(4)三维设计p48例1第(2)小题(3)方法总结:可以将向量当作是多项式中字母一样进行合并同类项等多项式的运算。式中的向量 就等同于字母的说法正确吗?为什么?不正确!向量 具有几何意义不能等同于字母。例5、计算:(课本p88) 练习:p90第5题 化简: 新课讲授(1)(2)(3)数乘向量与原向量之间的位置有什么关系?成立新课讲授知识点3、平面向量共线定理:思考:1)为什么 ?2) 可以是零向量吗?新课讲授ABC新课讲授强化训练ABC证明三点共线的方法:方法总结:AB=λBC 且有公共点BA,B,C三点共线新课讲授拓展探究:问题:例6中向量 能被向量 和向量 表示吗?
如果能,怎么表示?如果能,则可以被表示为则有即必有解之得:所以有问题改为 呢? 可以得:拓展探究:例7:已知A、B、P三点共线,O为直线外任意一点,若 求 的值 (三维设计例3第(2)题)平面向量三点共线定理:在平面中
A、B、C三点共线等价于 且1、知识回顾:
①向量数乘运算及运算律
②向量共线定理 向量a与b共线③定理的应用:
证明 三点共线:
AB=λBC
且有公共点B
2、数学思想方法:①数形结合思想;②化归转化思想A,B,C三点共线课堂小结4、已知 与 是不共线的向量,若
, , ,
若 三点共线,求 的值.课外探究
当 时, 的方向与 的方向相反;
当 时,知识点1、向量数乘运算: 新课讲授注意:①实数与向量的乘积等于一个向量;
②
③数乘运算不等同于向量的乘法。 向量向量的数乘(1)长度:知识点2、向量数乘运算律: 新课讲授新课讲授知识点2、向量数乘运算律: 知识点2、向量数乘运算律: 新课讲授向量的加、减、数乘运算统称为向量的线性运算.新课讲授知识点2、向量数乘运算律: 特别的: 和 一般的对于任意向量 、 ,以及任意实数
, 恒有新课讲授(1)(2)(4)三维设计p48例1第(2)小题(3)方法总结:可以将向量当作是多项式中字母一样进行合并同类项等多项式的运算。式中的向量 就等同于字母的说法正确吗?为什么?不正确!向量 具有几何意义不能等同于字母。例5、计算:(课本p88) 练习:p90第5题 化简: 新课讲授(1)(2)(3)数乘向量与原向量之间的位置有什么关系?成立新课讲授知识点3、平面向量共线定理:思考:1)为什么 ?2) 可以是零向量吗?新课讲授ABC新课讲授强化训练ABC证明三点共线的方法:方法总结:AB=λBC 且有公共点BA,B,C三点共线新课讲授拓展探究:问题:例6中向量 能被向量 和向量 表示吗?
如果能,怎么表示?如果能,则可以被表示为则有即必有解之得:所以有问题改为 呢? 可以得:拓展探究:例7:已知A、B、P三点共线,O为直线外任意一点,若 求 的值 (三维设计例3第(2)题)平面向量三点共线定理:在平面中
A、B、C三点共线等价于 且1、知识回顾:
①向量数乘运算及运算律
②向量共线定理 向量a与b共线③定理的应用:
证明 三点共线:
AB=λBC
且有公共点B
2、数学思想方法:①数形结合思想;②化归转化思想A,B,C三点共线课堂小结4、已知 与 是不共线的向量,若
, , ,
若 三点共线,求 的值.课外探究
