2.3.1 向量数量积的物理背景与定义 课件(23张PPT)
文档属性
| 名称 | 2.3.1 向量数量积的物理背景与定义 课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 845.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-30 08:33:57 | ||
图片预览






文档简介
课件23张PPT。第二章 平面向量
2.3.1 向量数量积的物理背景与定义学习目标【知识目标】
理解两个向量的夹角和向量在轴上的正射影的概念
掌握平面向量数量积的定义及性质,理解其几何意义.并能进行相关的运算和判断.
【能力目标】
通过学习体会“数”与“形”的结合,培养分析问题
解决问题的能力
【情感目标】
通过熟悉的物理背景去感知数学问题,体会向量在
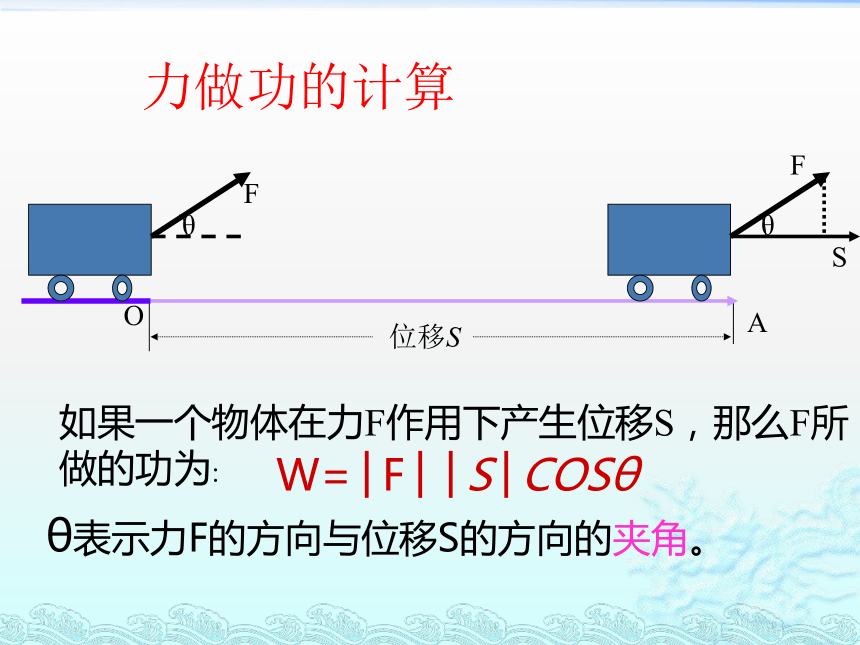
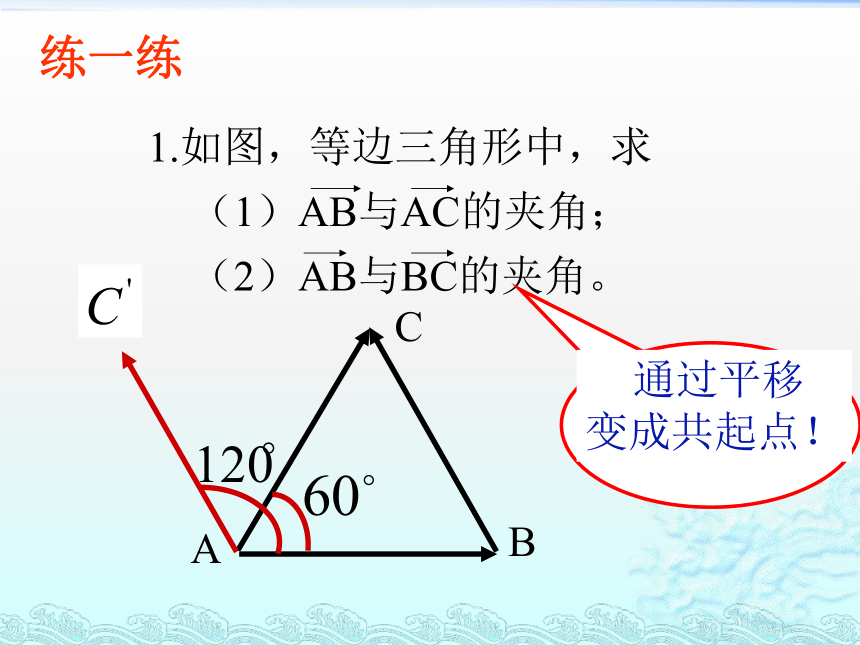
物理中的应用如果一个物体在力F作用下产生位移S,那么F所做的功为:θ表示力F的方向与位移S的方向的夹角。W=│F││S│COSθ力做功的计算一、两个向量的夹角(1)求两向量的夹角,应保证两个向量有公共起点,若没有,须平移使它们有公共起点;(5)规定:在讨论垂直问题时,零向量与任意向量垂直.几点说明一练一练二、向量在轴上的正射影 (2)正射影的数量: 1. a在轴l上的数量或在轴l方向上的数量是一个数量,不是向量.
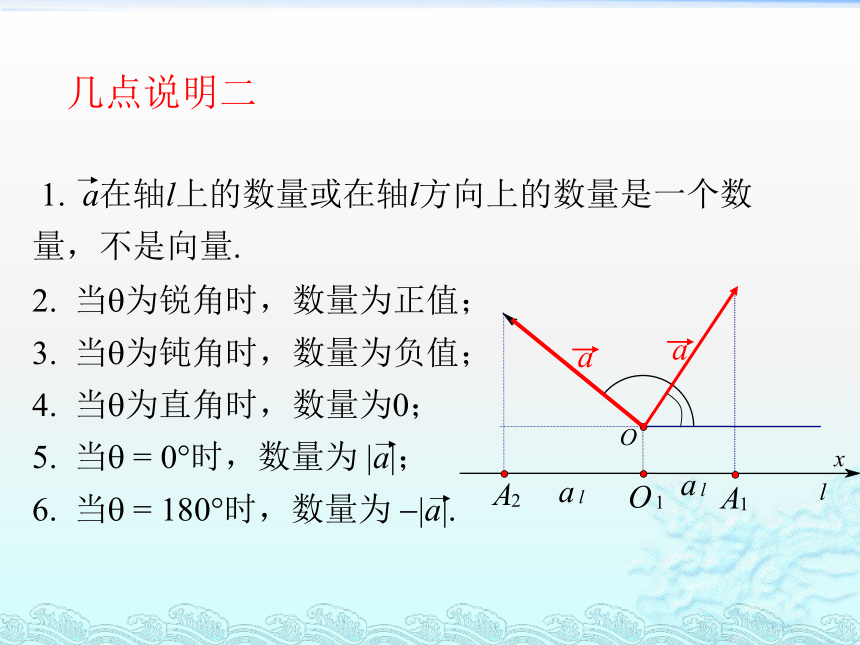
2. 当?为锐角时,数量为正值;
3. 当?为钝角时,数量为负值;
4. 当?为直角时,数量为0;
5. 当? = 0?时,数量为 |a|;
6. 当? = 180?时,数量为 ?|a|. 几点说明二xlO2.已知轴l解:OA1=5COS600=5×( ?)=5/2-5/2练一练三、向量的数量积(内积) 定义: 叫做向量a和b的数量积(或内积)
记作:a·b .
即 a·b = 几点说明三1.a · b不能写成a×b ,ab .θ为锐角时,
| b | cosθ>0θ为钝角时,
| b | cosθ<0θ为直角时,
| b | cosθ=0两个向量的数量积的性质:内积为零是判定两向量垂直的条件用于计算向量的模用于计算向量的夹角,
以及判断三角形的形状3.已知|a|=5,|b|=4,=120°,求a·b.
解: a?b =|a|·|b|cos
=5×4×cos120°
= -10. 练一练合作探究、展示、点评探究、展示、点评要求:
1、自我纠错 2分钟,用红色笔记录好学案中出现的疑难问题;
2、分组讨论交流,针对学案上疑难问题进行讨论;
3、展示小组讨论完毕后到黑板展示;
4、点评小组组织好发言要点,展示小组展示完毕后
到黑板写出点评要点,准备黑板点评
小组分工:A 锐角三角形C 钝角三角形D 不能确定B 直角三角形DCA 锐角三角形B 直角三角形C 钝角三角形D 不能确定拓展例2课堂小结1.两个向量的夹角2.向量在轴上的正射影 正射影的数量3.向量的数量积(内积) 4.两个向量的数量积的性质:当堂检测答案:总结整理
完善学案
2.3.1 向量数量积的物理背景与定义学习目标【知识目标】
理解两个向量的夹角和向量在轴上的正射影的概念
掌握平面向量数量积的定义及性质,理解其几何意义.并能进行相关的运算和判断.
【能力目标】
通过学习体会“数”与“形”的结合,培养分析问题
解决问题的能力
【情感目标】
通过熟悉的物理背景去感知数学问题,体会向量在
物理中的应用如果一个物体在力F作用下产生位移S,那么F所做的功为:θ表示力F的方向与位移S的方向的夹角。W=│F││S│COSθ力做功的计算一、两个向量的夹角(1)求两向量的夹角,应保证两个向量有公共起点,若没有,须平移使它们有公共起点;(5)规定:在讨论垂直问题时,零向量与任意向量垂直.几点说明一练一练二、向量在轴上的正射影 (2)正射影的数量: 1. a在轴l上的数量或在轴l方向上的数量是一个数量,不是向量.
2. 当?为锐角时,数量为正值;
3. 当?为钝角时,数量为负值;
4. 当?为直角时,数量为0;
5. 当? = 0?时,数量为 |a|;
6. 当? = 180?时,数量为 ?|a|. 几点说明二xlO2.已知轴l解:OA1=5COS600=5×( ?)=5/2-5/2练一练三、向量的数量积(内积) 定义: 叫做向量a和b的数量积(或内积)
记作:a·b .
即 a·b = 几点说明三1.a · b不能写成a×b ,ab .θ为锐角时,
| b | cosθ>0θ为钝角时,
| b | cosθ<0θ为直角时,
| b | cosθ=0两个向量的数量积的性质:内积为零是判定两向量垂直的条件用于计算向量的模用于计算向量的夹角,
以及判断三角形的形状3.已知|a|=5,|b|=4,
解: a?b =|a|·|b|cos
=5×4×cos120°
= -10. 练一练合作探究、展示、点评探究、展示、点评要求:
1、自我纠错 2分钟,用红色笔记录好学案中出现的疑难问题;
2、分组讨论交流,针对学案上疑难问题进行讨论;
3、展示小组讨论完毕后到黑板展示;
4、点评小组组织好发言要点,展示小组展示完毕后
到黑板写出点评要点,准备黑板点评
小组分工:A 锐角三角形C 钝角三角形D 不能确定B 直角三角形DCA 锐角三角形B 直角三角形C 钝角三角形D 不能确定拓展例2课堂小结1.两个向量的夹角2.向量在轴上的正射影 正射影的数量3.向量的数量积(内积) 4.两个向量的数量积的性质:当堂检测答案:总结整理
完善学案
