2.3.3 向量数量积的坐标运算与度量公式 课件(17张PPT)
文档属性
| 名称 | 2.3.3 向量数量积的坐标运算与度量公式 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 323.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-30 00:00:00 | ||
图片预览





文档简介
课件17张PPT。2.3.3 向量数量积的坐标运算
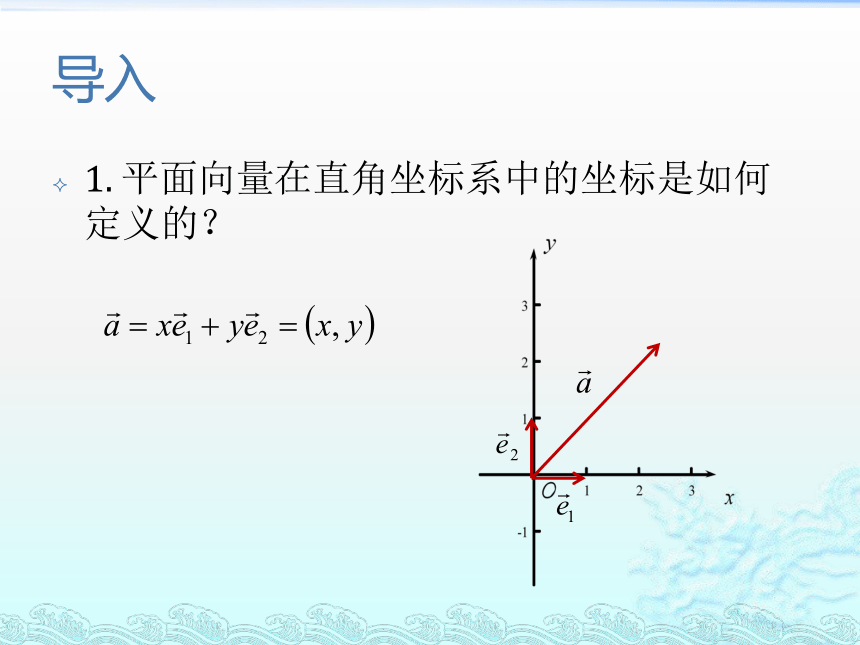
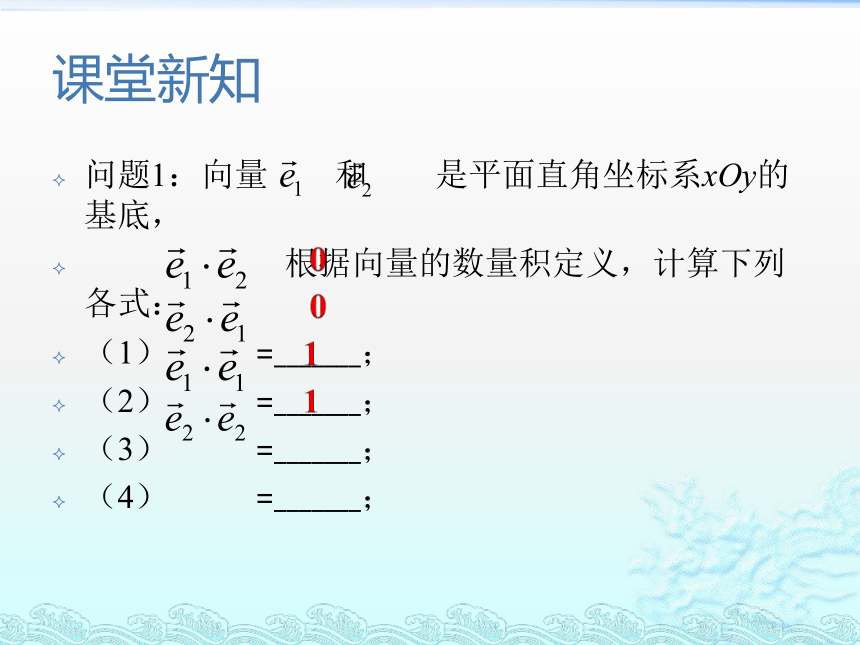
与度量公式导入1. 平面向量在直角坐标系中的坐标是如何定义的?2.平面向量数量积的定义?课堂新知问题1:向量 和 是平面直角坐标系xOy的基底,
根据向量的数量积定义,计算下列各式:
(1) =_______;
(2) =_______;
(3) =_______;
(4) =_______;
1100问题2:已知两个向量 , ,
怎样用 和 的坐标表示 呢?结论:两个向量的数量积等于对应坐标的乘积的和问题3:应用向量数量积的坐标表达式,思考下列问题:(1)设 = (x,y),则 =_______, | | = _________ .(2)设A、B 两点的坐标分别为 ( , ),( , ),
则 | | =____________________(3)设 =( , )、 =( , ),则cos =_______2.向量的长度、距离和夹角公式(1)向量的长度设 ,则结论:向量的长度等于它的坐标的平方和的算术平方根 设A、B 两点的坐标分别为 ( , ),( , ),
则 的长度是A、B两点之间的距离2.向量的长度、距离和夹角公式(2)向量的夹角公式 由向量数量积的坐标表达式和向量长度计算公式,以及向量数量积的定义,得两向量夹角余弦的坐标表达式:例1. , ,求 , , ,例2. 已知点A(1, 2),B (3, 4),C (5,0),求
∠BAC的正弦值.问题4:根据向量数量积的性质可知, 设 , 则 问题5:设 ,两向量 什么关系?与 垂
直的所有向量如何表示?例 3.已知 A (1, 2),B (2, 3),C ( 2, 5),求证: △ABC
是直角三角形。注:两个向量的数量积是否为零,是判断相应的两条直线是否垂直的重要方法之一练习1. 在△ABC 中 ,若△ABC 为直角三角形,
求 k 的值. 2. 写出与下列向量垂直的单位向量:
(1) = (3,4) (2) = (-1,1)3. 已知向量 = (3,3), = (-2,5),求 在 方向上的
正射影的数量。课堂小结1. 两个向量的数量积等于它们对应坐标的乘积的和。2. 设 , ,则3. 设 , 为非零向量,则作业练习册
根据向量的数量积定义,计算下列各式:
(1) =_______;
(2) =_______;
(3) =_______;
(4) =_______;
1100问题2:已知两个向量 , ,
怎样用 和 的坐标表示 呢?结论:两个向量的数量积等于对应坐标的乘积的和问题3:应用向量数量积的坐标表达式,思考下列问题:(1)设 = (x,y),则 =_______, | | = _________ .(2)设A、B 两点的坐标分别为 ( , ),( , ),
则 | | =____________________(3)设 =( , )、 =( , ),则cos =_______2.向量的长度、距离和夹角公式(1)向量的长度设 ,则结论:向量的长度等于它的坐标的平方和的算术平方根 设A、B 两点的坐标分别为 ( , ),( , ),
则 的长度是A、B两点之间的距离2.向量的长度、距离和夹角公式(2)向量的夹角公式 由向量数量积的坐标表达式和向量长度计算公式,以及向量数量积的定义,得两向量夹角余弦的坐标表达式:例1. , ,求 , , ,例2. 已知点A(1, 2),B (3, 4),C (5,0),求
∠BAC的正弦值.问题4:根据向量数量积的性质可知, 设 , 则 问题5:设 ,两向量 什么关系?与 垂
直的所有向量如何表示?例 3.已知 A (1, 2),B (2, 3),C ( 2, 5),求证: △ABC
是直角三角形。注:两个向量的数量积是否为零,是判断相应的两条直线是否垂直的重要方法之一练习1. 在△ABC 中 ,若△ABC 为直角三角形,
求 k 的值. 2. 写出与下列向量垂直的单位向量:
(1) = (3,4) (2) = (-1,1)3. 已知向量 = (3,3), = (-2,5),求 在 方向上的
正射影的数量。课堂小结1. 两个向量的数量积等于它们对应坐标的乘积的和。2. 设 , ,则3. 设 , 为非零向量,则作业练习册
