2.1平面向量的实际背景及基本概念 课件(20张PPT)
文档属性
| 名称 | 2.1平面向量的实际背景及基本概念 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-30 00:00:00 | ||
图片预览




文档简介
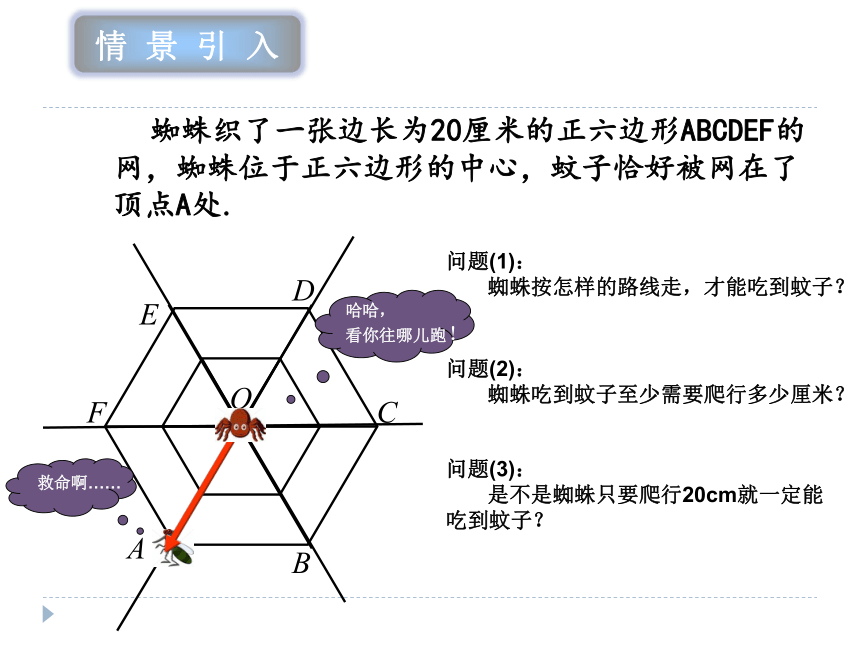
课件20张PPT。物体在某一段时间内,如果由初位置移到末位置,则由初位置到末位置的有向线段叫做位移。 2.1向量的实际背景及基本概念 蜘蛛织了一张边长为20厘米的正六边形ABCDEF的网,蜘蛛位于正六边形的中心,蚊子恰好被网在了顶点A处.问题(1):
蜘蛛按怎样的路线走,才能吃到蚊子?问题(2):
蜘蛛吃到蚊子至少需要爬行多少厘米?问题(3):
是不是蜘蛛只要爬行20cm就一定能吃到蚊子?哈哈,
看你往哪儿跑!救命啊……
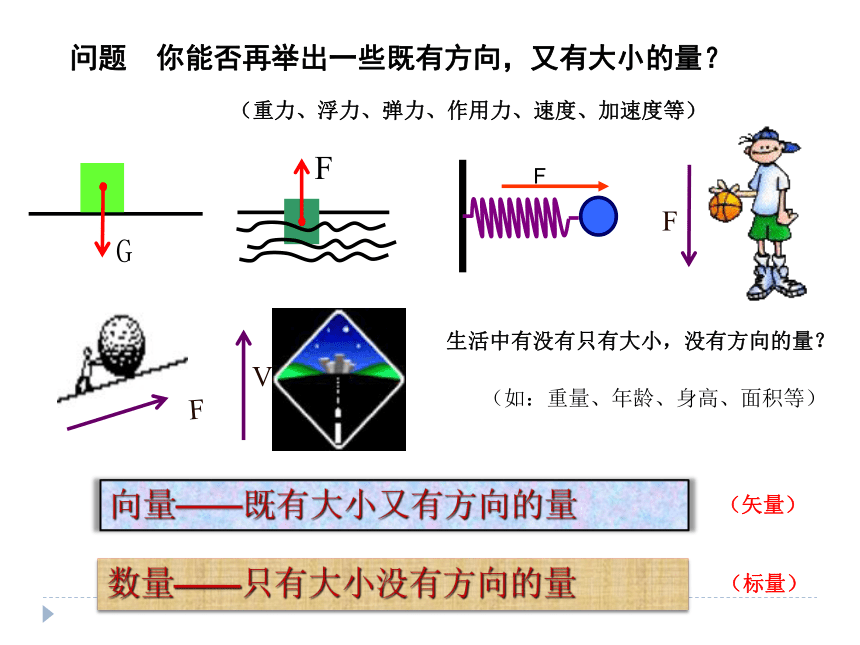
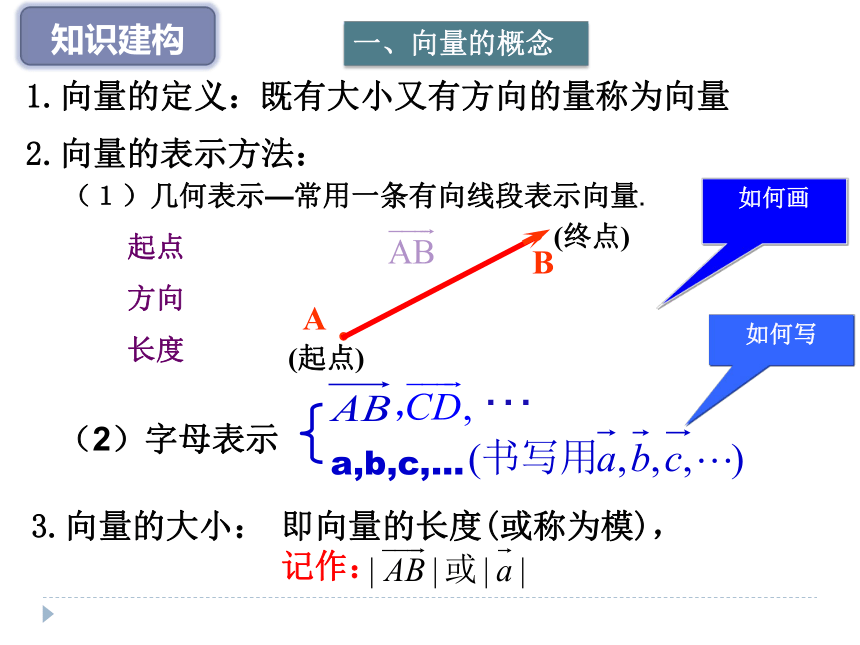
问题 你能否再举出一些既有方向,又有大小的量?生活中有没有只有大小,没有方向的量?(如:重量、年龄、身高、面积等)(重力、浮力、弹力、作用力、速度、加速度等)向量——既有大小又有方向的量数量——只有大小没有方向的量(矢量)(标量)物体在某一段时间内,如果由初位置移到末位置,则由初位置到末位置的有向线段叫做位移。 一.向量的概念及表示1.向量的定义:既有大小又有方向的量称为向量2.向量的表示方法:3.向量的大小:知识建构如何画如何写(1)几何表示—常用一条有向线段表示向量...AB(起点)(终点)起点
方向
长度(2)字母表示一、向量的概念即向量的长度(或称为模),
记作: 我们所说的向量,与起点无关,用有向线段表示向量时,起点可以
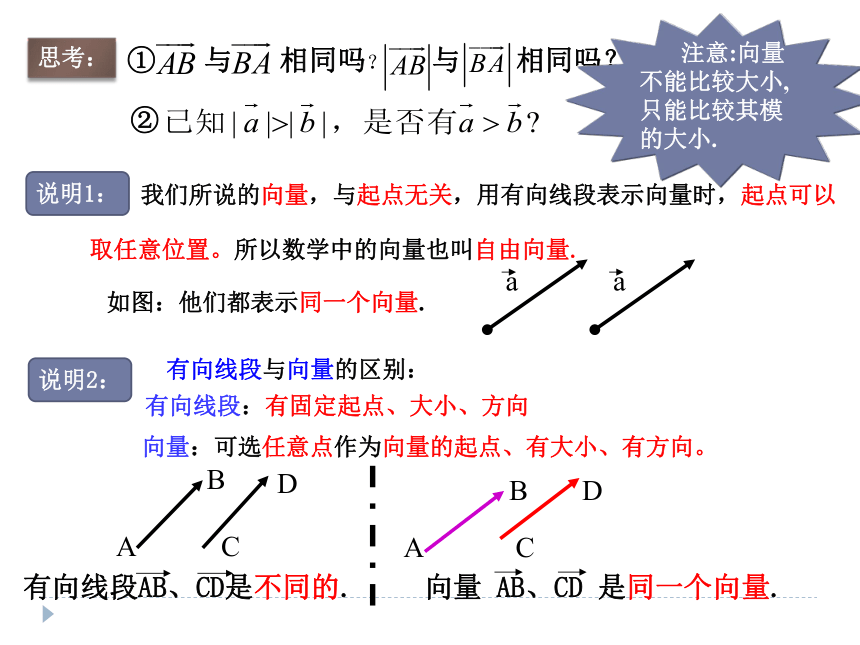
取任意位置。所以数学中的向量也叫自由向量.如图:他们都表示同一个向量.说明1:思考:① 与 相同吗? 与 相同吗?②有向线段与向量的区别:有向线段:有固定起点、大小、方向向量:可选任意点作为向量的起点、有大小、有方向。说明2:4.两个特殊向量:(1)零向量
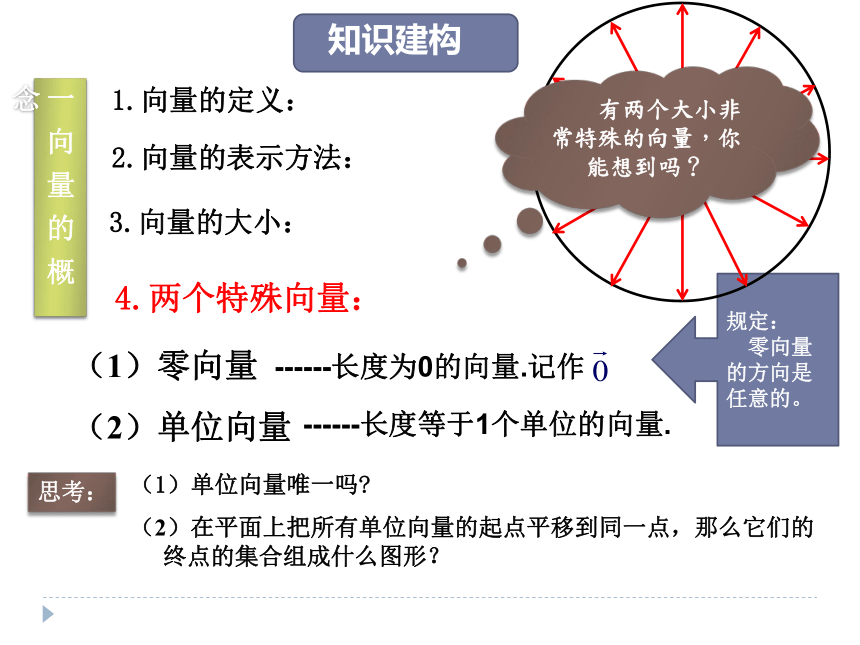
(2)单位向量知识建构1.向量的定义:2.向量的表示方法:3.向量的大小:------长度为0的向量.记作 ------长度等于1个单位长度的向量. 有两个大小非常特殊的向量,你能想到吗?规定:
零向量的方向是任意的。一 向 量 的 概 念4.两个特殊向量:(1)零向量
(2)单位向量------长度为0的向量.记作 ------长度等于1个单位的向量.思考:规定:
零向量的方向是任意的。(1)单位向量唯一吗?
(2)在平面上把所有单位向量的起点平移到同一点,那么它们的终点的集合组成什么图形?
一 向 量 的 概 念1.向量的定义:2.向量的表示方法:3.向量的大小: 有两个大小非常特殊的向量,你能想到吗? 观察图中的正六边形ABCDEF.给图中的任意两个线段加上箭头表示向量,说说你所标注的向量之间有怎样的关系? 你是怎样研究的? 探究:向量与向量之间的关系?方向相同,大小相等 方向相同,大小不相等 方向相反,大小相等 方向相反,大小不相等 方向既不相同也不相反
大小相等方向既不相同也不相反
大小不相等相等相等不相等不相等平行向量
------方向相同或相反的非零向量.
记作:如:方向相同,大小相等 方向相同,大小不相等 方向相反,大小相等 方向相反,大小不相等 方向既不相同也不相反
大小相等方向既不相同也不相反
大小不相等方向相同;大小方向相反;大小相等相等不相等不相等特殊向量:平行向量
------方向相同或相反的非零向量.
记作:相等向量------长度相等且方向相同的向量.相反向量------长度相等且方向相反的向量.二.向量之间的关系 规定:零向量与任一向量平行.2.相等向量------长度相等且方向相同的向量.1.平行向量 ------方向相同或相反的非零向量.规定:零向量和零向量相等.思考:单位向量和单位向量一定相等吗?3.相反向量------长度相等且方向相反的向量.(记作 : )(记作: )(记作: )知识建构4.共线向量与平行向量的关系平行向量就是共线向量,共线向量就是平行向量!知识建构 说明:我们所研究的向量为自由向量,只与大小和方向有关,与有向线段的起点位置无关,有向线段只是向量的一种几何表示!向量向量的概念向量的定义表示方法零向量相等向量平行(共线)向量相反向量知识建构单位向量向量的关系30秒后你将接受挑战!你准备好了吗?!1.如图, D、E、F分别是△ABC各边上的中点,在以A、B、C、D、E、F为端点的有向线段表示的向量中,请分别写出: (1)与向量 相等的向量有__个,
分别是___________; (2)与向量 的模相等的向量有__个,
分别是 _________________;(3)与向量 方向相反的向量有___个,
分别是_____________________.254小试牛刀概念辨析2.判断下列命题是否正确,若不正确,请简述理由.(6)模相等的两个平行向量是相等的向量;(7)共线向量一定在同一直线上;温馨提示:
1.做题时要注意向量平行(共线)与直线平行、共线的区别
2.不要忽略零向量的特殊性及有关的两个规定(1)与非零向量 平行的单位向量有无数个;(2)若 则 ;(3)若 则 ;(4)若 ,则 ;(5)若 则 ;( )( )( )( )( )( )( )××××××向量向量的概念向量的定义表示方法零向量相等向量平行(共线)向量相反向量小结知识要点单位向量向量的关系2.思考题.如图,以1 3方格中的格点为起点和终点的所有向量中,有多少种大小不同的模?有多少种不同的方向?
作业:1.课本P77习题2.1 第1、2小题谢谢指导!
(备用)3.在如图所示的向量 , , , , 中(小正方形的边长为1),是否存在:
(1)共线向量? (2)相反向量?
(3)相等向量? (4)模相等的向量?
若存在,分别写出这些向量.
蜘蛛按怎样的路线走,才能吃到蚊子?问题(2):
蜘蛛吃到蚊子至少需要爬行多少厘米?问题(3):
是不是蜘蛛只要爬行20cm就一定能吃到蚊子?哈哈,
看你往哪儿跑!救命啊……
问题 你能否再举出一些既有方向,又有大小的量?生活中有没有只有大小,没有方向的量?(如:重量、年龄、身高、面积等)(重力、浮力、弹力、作用力、速度、加速度等)向量——既有大小又有方向的量数量——只有大小没有方向的量(矢量)(标量)物体在某一段时间内,如果由初位置移到末位置,则由初位置到末位置的有向线段叫做位移。 一.向量的概念及表示1.向量的定义:既有大小又有方向的量称为向量2.向量的表示方法:3.向量的大小:知识建构如何画如何写(1)几何表示—常用一条有向线段表示向量...AB(起点)(终点)起点
方向
长度(2)字母表示一、向量的概念即向量的长度(或称为模),
记作: 我们所说的向量,与起点无关,用有向线段表示向量时,起点可以
取任意位置。所以数学中的向量也叫自由向量.如图:他们都表示同一个向量.说明1:思考:① 与 相同吗? 与 相同吗?②有向线段与向量的区别:有向线段:有固定起点、大小、方向向量:可选任意点作为向量的起点、有大小、有方向。说明2:4.两个特殊向量:(1)零向量
(2)单位向量知识建构1.向量的定义:2.向量的表示方法:3.向量的大小:------长度为0的向量.记作 ------长度等于1个单位长度的向量. 有两个大小非常特殊的向量,你能想到吗?规定:
零向量的方向是任意的。一 向 量 的 概 念4.两个特殊向量:(1)零向量
(2)单位向量------长度为0的向量.记作 ------长度等于1个单位的向量.思考:规定:
零向量的方向是任意的。(1)单位向量唯一吗?
(2)在平面上把所有单位向量的起点平移到同一点,那么它们的终点的集合组成什么图形?
一 向 量 的 概 念1.向量的定义:2.向量的表示方法:3.向量的大小: 有两个大小非常特殊的向量,你能想到吗? 观察图中的正六边形ABCDEF.给图中的任意两个线段加上箭头表示向量,说说你所标注的向量之间有怎样的关系? 你是怎样研究的? 探究:向量与向量之间的关系?方向相同,大小相等 方向相同,大小不相等 方向相反,大小相等 方向相反,大小不相等 方向既不相同也不相反
大小相等方向既不相同也不相反
大小不相等相等相等不相等不相等平行向量
------方向相同或相反的非零向量.
记作:如:方向相同,大小相等 方向相同,大小不相等 方向相反,大小相等 方向相反,大小不相等 方向既不相同也不相反
大小相等方向既不相同也不相反
大小不相等方向相同;大小方向相反;大小相等相等不相等不相等特殊向量:平行向量
------方向相同或相反的非零向量.
记作:相等向量------长度相等且方向相同的向量.相反向量------长度相等且方向相反的向量.二.向量之间的关系 规定:零向量与任一向量平行.2.相等向量------长度相等且方向相同的向量.1.平行向量 ------方向相同或相反的非零向量.规定:零向量和零向量相等.思考:单位向量和单位向量一定相等吗?3.相反向量------长度相等且方向相反的向量.(记作 : )(记作: )(记作: )知识建构4.共线向量与平行向量的关系平行向量就是共线向量,共线向量就是平行向量!知识建构 说明:我们所研究的向量为自由向量,只与大小和方向有关,与有向线段的起点位置无关,有向线段只是向量的一种几何表示!向量向量的概念向量的定义表示方法零向量相等向量平行(共线)向量相反向量知识建构单位向量向量的关系30秒后你将接受挑战!你准备好了吗?!1.如图, D、E、F分别是△ABC各边上的中点,在以A、B、C、D、E、F为端点的有向线段表示的向量中,请分别写出: (1)与向量 相等的向量有__个,
分别是___________; (2)与向量 的模相等的向量有__个,
分别是 _________________;(3)与向量 方向相反的向量有___个,
分别是_____________________.254小试牛刀概念辨析2.判断下列命题是否正确,若不正确,请简述理由.(6)模相等的两个平行向量是相等的向量;(7)共线向量一定在同一直线上;温馨提示:
1.做题时要注意向量平行(共线)与直线平行、共线的区别
2.不要忽略零向量的特殊性及有关的两个规定(1)与非零向量 平行的单位向量有无数个;(2)若 则 ;(3)若 则 ;(4)若 ,则 ;(5)若 则 ;( )( )( )( )( )( )( )××××××向量向量的概念向量的定义表示方法零向量相等向量平行(共线)向量相反向量小结知识要点单位向量向量的关系2.思考题.如图,以1 3方格中的格点为起点和终点的所有向量中,有多少种大小不同的模?有多少种不同的方向?
作业:1.课本P77习题2.1 第1、2小题谢谢指导!
(备用)3.在如图所示的向量 , , , , 中(小正方形的边长为1),是否存在:
(1)共线向量? (2)相反向量?
(3)相等向量? (4)模相等的向量?
若存在,分别写出这些向量.
