2.3.2 向量数量积的运算律 课件(21张PPT)
文档属性
| 名称 | 2.3.2 向量数量积的运算律 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 17.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-30 08:25:09 | ||
图片预览








文档简介
课件21张PPT。复习:2.正射影的概念及数量积的几何意义1.向量数量积的定义 的正射影在轴l上的坐标,
称作 在轴l上的数量或在轴l方向上的数量。但目前为止,我们没有办法研究:思考:在实数运算与多项式运算中
ab=ba;
(a+b)·c=ac+bc
(a+b)(c+d)=ac+ad+bc+bd
......
如果向量要进行这样的运算,规则是什么呢?§2.3.2 向量数量积的运算律【学习目标】
1.掌握向量数量积的几个运算律,了解投影与数量积运算规则的关系。
2.经历向量数量积运算律的探究,发现解决复杂向量数量积运算的方法。
3.自主思维,勇于探索,敢于质疑,发展直观想象和逻辑推理。结合向量数量积定义的知识
试验证 交换律我们希望向量数量积的运算律,
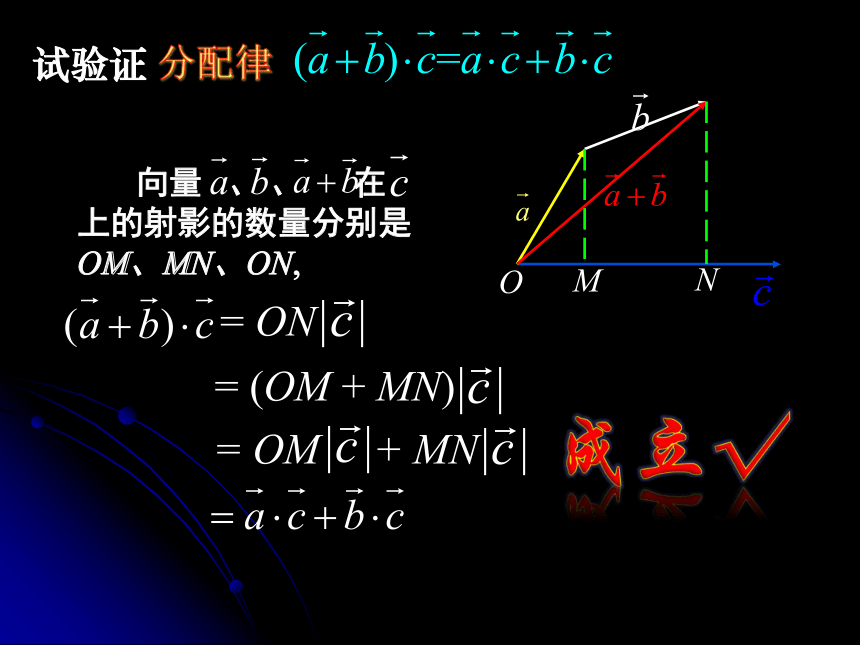
与实数的乘法一致,但事实确实如此?成立√试验证 数乘结合律成立√λ>0λ<0ONM试验证 分配律 向量 、 、 在 上的射影的数量分别是OM、MN、ON, = ON = (OM + MN) = OM + MN成立√根据以上运算律试探究:试验证 结合律不成立×试验证 不成立×练习:【练习】运用向量数量积运算律进行计算
【练习】概念辨析【练习】运用向量数量积解决几何问题
1.向量法证明勾股定理B
A
C
2.向量法解三角形未知量(2018·高考)已知向量a,b满足,|a|=1,a·b=-1,则a·(2a-b)=
A.4 B.3 C.2 D.0答案:B小结:
尾巴方法:求一个向量的模,可以先平方,再求算数平方根
1.遇到解决不了的数学问题,作图试试有大概率会突破。
2.不仅仅会举一反三,还要举一思三,三思后行。
3.数学是一门严谨的学科,思考问题时一定要小心有没有漏掉细节。探无止境试用向量法证明三角形余弦定理:
c2=a2+b2-2ab cosC
a2=b2+c2-2bc cosA
b2=a2+c2-2ac cosB作业60号导学案,练习册P50
称作 在轴l上的数量或在轴l方向上的数量。但目前为止,我们没有办法研究:思考:在实数运算与多项式运算中
ab=ba;
(a+b)·c=ac+bc
(a+b)(c+d)=ac+ad+bc+bd
......
如果向量要进行这样的运算,规则是什么呢?§2.3.2 向量数量积的运算律【学习目标】
1.掌握向量数量积的几个运算律,了解投影与数量积运算规则的关系。
2.经历向量数量积运算律的探究,发现解决复杂向量数量积运算的方法。
3.自主思维,勇于探索,敢于质疑,发展直观想象和逻辑推理。结合向量数量积定义的知识
试验证 交换律我们希望向量数量积的运算律,
与实数的乘法一致,但事实确实如此?成立√试验证 数乘结合律成立√λ>0λ<0ONM试验证 分配律 向量 、 、 在 上的射影的数量分别是OM、MN、ON, = ON = (OM + MN) = OM + MN成立√根据以上运算律试探究:试验证 结合律不成立×试验证 不成立×练习:【练习】运用向量数量积运算律进行计算
【练习】概念辨析【练习】运用向量数量积解决几何问题
1.向量法证明勾股定理B
A
C
2.向量法解三角形未知量(2018·高考)已知向量a,b满足,|a|=1,a·b=-1,则a·(2a-b)=
A.4 B.3 C.2 D.0答案:B小结:
尾巴方法:求一个向量的模,可以先平方,再求算数平方根
1.遇到解决不了的数学问题,作图试试有大概率会突破。
2.不仅仅会举一反三,还要举一思三,三思后行。
3.数学是一门严谨的学科,思考问题时一定要小心有没有漏掉细节。探无止境试用向量法证明三角形余弦定理:
c2=a2+b2-2ab cosC
a2=b2+c2-2bc cosA
b2=a2+c2-2ac cosB作业60号导学案,练习册P50
