向量数量积 课件(40张PPT)
图片预览











文档简介
课件40张PPT。§2.4.1
平面向量的数量积 问题1:前面我们已经研究了向量的哪些运算?向量有
“乘法”吗?两个向量可以“相乘”吗? 问题2:我们是怎样引入向量的加法运算的?
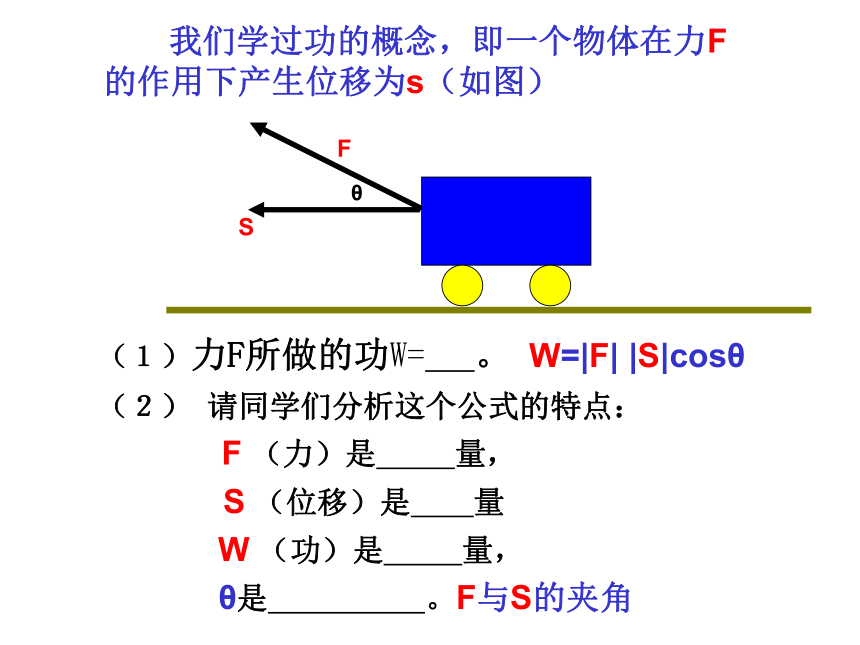
我们又是按照怎样的顺序研究这种运算的?1.创设情景 我们学过功的概念,即一个物体在力F的作用下产生位移为s(如图)θFS(2) 请同学们分析这个公式的特点:
F (力)是 量,
S (位移)是 量
W (功)是 量,
θ是 。F与S的夹角
(1)力F所做的功W= 。 W=|F| |S|cosθ 问题3:你能用文字语言来表述功的计算公式吗?如果我们将公式中的力与位移推广到一般向量,其结果又该如何表述? 功是力与位移的大小及其夹角余弦的乘积;
结果是两个向量的大小及其夹角余弦的乘积。 2.定义探究平面向量的数量积规定:零向量与任一向量的数量积为 0 .思考并回答下列问题1.向量夹角的取值范围是什么?
2.影响数量积大小的因素有哪些?
3.向量的数量积运算与线性(加减法、数乘)
运算的结果有什么区别?
4. 向量投影的概念和取值范围是什么?
5.数量积的几何意义是什么?
(1)定义 :(2)定义的说明:1.数量积的定义正0负2.数量积的性质3.性质探究 问题4: 我们学过了实数乘法的哪些运算律?
a,b为实数①交换律:ab=ba
②结合律:(ab)c=a(bc)
③分配律:(a+b)c=ac+bc
④ ac=bc且c不为0,则a=b4.运算律探究对于向量还成立吗?自主探究,合作交流3、数量积的运算律 已知向量 和实数λ,则:课后学生独立证明运算律5.应用与提高6.小结与作业作业: 课本P108习题2.4A组1、2、3。
已知 与 都是非零向量,且 与
垂直, 与 垂直,求 与 的夹角。7.拓展与提高谢谢大家!
再见!例题例1 已知|a|=5, |b|=4, a与b的夹角θ=120o,求a·b.练习P106作业:
课本P108习题2.4A组1、2、3。?练习:三、讲解范例:
例1 已知|a|=5, |b|=4, a与b的夹角θ=120o,求a·b.
例2 已知|a|=6, |b|=4, a与b的夹角为60o求(a+2b)·(a-3b).
例3 已知|a|=3, |b|=4, 且a与b不共线,k为何值时,
向量a+kb与a-kb互相垂直.
例4 判断正误,并简要说明理由.
①a·0=0;②0·a=0;③0-=④|a·b|=|a||b|;
⑤若a≠0,则对任一非零b有a·b≠0;
⑥a·b=0,则a与b中至少有一个为0;
⑦对任意向量a,b,с都有(a·b) ·c= a·(b ·c)
⑧a与b是两个单位向量,则a2=b2.小结:1.
2.可用来求向量的模3.投影作业:学习目标:
1.掌握平面向量的数量积及其几何意义;
2.掌握平面向量数量积的重要性质及运算律;
3.了解用平面向量的数量积可以处理有关长度、角度和垂直的问题; 4.掌握向量垂直的条件.$﹫·一、复习引入:1. 向量共线定理 2.平面向量基本定理 3.平面向量的坐标表示4.平面向量的坐标运算5.∥ (?)的条件 6.两个非零向量夹角的概念
(1) 两个向量的数量积是一个数量,其大小由两个向量的长度及夹角决定. 此点很重要定义理解注:
(1)两个向量的数量积与实数同向量的积的区别:
两个向量的数量积是一个实数,不是向量,符号
由cos?的符号所决定,而实数同向量的积是一个向量
. 1. 两个向量的数量积是一个实数,不是向量,符号
由cos?的符号所决定,而实数同向量的积是一个向量2.两个向量的数量积称为内积,写成a?b;今后要学到两个向量的外积a×b,
而a?b是两个向量的数量的积,书写时要严格区分.符号“· ”在向量运算中不是乘号,
既不能省略,也不能用“×”代替.(1)定义 :(2)定义的简单说明:1.数量积的定义 问题4:向量的数量积运算与线性(加减法、数乘)运算的结果有什么不同?影响数量积大小的因素有哪些?并完成下表:2.研究数量积的几何意义(1)给出向量投影的概念(2)问题6:数量积的几何意义是什么?(1)定义 :(2)定义的简单说明:2、明晰数量积的定义 问题5:向量的数量积运算与线性(加减法、数乘)运算的结果有什么不同?影响数量积大小的因素有哪些?并完成下表:返回2.平面向量数量积(内积)的定义:已知两个非零向量a与b,
它们的夹角是θ,则数量|a||b|cos?叫a与b的数量积,
记作a?b,即有a?b = |a||b|cos?,
(0≤θ≤π).并规定0与任何向量的数量积为0.?探究:1.两个向量的数量积与同实数积有什么区别?2.两个向量的数量积与实数同向量的积有什么区别?返回(1)两个向量的数量积是一个实数,不是向量,符号由cos?的符号所决定.
(2)两个向量的数量积称为内积,写成a?b;今后要学到两个向量的外积a×b,
而a?b是两个向量的数量的积,书写时要严格区分.符号“· ”在向量运算中不是乘号,
既不能省略,也不能用“×”代替.
(3)在实数中,若a?0,且a?b=0,则b=0;但是在数量积中,若a?0,且a?b=0,
不能推出b=0.因为其中cos?有可能为0.
(4)已知实数a、b、c(b?0),则ab=bc ? a=c.但是a?b = b?c不能
得到 a=c
如右图:a?b = |a||b|cos? = |b||OA|,b?c = |b||c|cos? = |b||OA|
? a?b = b?c 但a ? c
(5)在实数中,有(a?b)c = a(b?c),但是(a?b)c ? a(b?c)
显然,这是因为左端是与c共线的向量,而右端是与a共线的向量,
而向量a与c不一定共线.两个向量的数量积与同实数积的区别两个向量的数量积与实数同向量的积的区别 两个向量的数量积是一个实数,不是向量,符号
由cos?的符号所决定,而实数同向量的积是一个向量 回忆两个向量的夹角返回概念:作3.“投影”的图
定义:|b|cos?叫做向量b在a方向上的投影.
投影也是一个数量,不是向量;当?为锐角时投影为正值;
当?为钝角时投影为负值;当?为直角时投影为0;当? = 0?时投影
为 |b|;当? = 180?时投影为 ?|b|.
返回4.向量的数量积的几何意义:
数量积a?b等于a的长度与b在a方向上投影|b|cos?的乘积.
5.两个向量的数量积的性质:
设a、b为两个非零向量,e是与b同向的单位向量.1? e?a = a?e =|a|cos?
2? a?b ? a?b = 0
3? 当a与b同向时,a?b = |a||b|;当a与b反向时,a?b = ?|a||b|.
特别的a?a = |a|2或4? cos? =5? |a?b| ≤ |a||b| 4. 向量的投影的概念 注意:当 q 为锐角时,投影是正值:当 q 为钝角时,投影是负值;当 q = 90° 时, 投影是 0 . 当q = 0o 时,投影为 ;
当q = 180°时,投影为 . (2) 两个向量数量积的几何意义思考并回答下列问题1.向量夹角的取值范围?
2.影响数量积大小的因素有哪些?
3.向量的数量积运算与线性(加减法、数乘)
运算的结果有什么区别?
4. 向量投影的概念?投影的取值范围?
5.平面向量的几何意义?
“乘法”吗?两个向量可以“相乘”吗? 问题2:我们是怎样引入向量的加法运算的?
我们又是按照怎样的顺序研究这种运算的?1.创设情景 我们学过功的概念,即一个物体在力F的作用下产生位移为s(如图)θFS(2) 请同学们分析这个公式的特点:
F (力)是 量,
S (位移)是 量
W (功)是 量,
θ是 。F与S的夹角
(1)力F所做的功W= 。 W=|F| |S|cosθ 问题3:你能用文字语言来表述功的计算公式吗?如果我们将公式中的力与位移推广到一般向量,其结果又该如何表述? 功是力与位移的大小及其夹角余弦的乘积;
结果是两个向量的大小及其夹角余弦的乘积。 2.定义探究平面向量的数量积规定:零向量与任一向量的数量积为 0 .思考并回答下列问题1.向量夹角的取值范围是什么?
2.影响数量积大小的因素有哪些?
3.向量的数量积运算与线性(加减法、数乘)
运算的结果有什么区别?
4. 向量投影的概念和取值范围是什么?
5.数量积的几何意义是什么?
(1)定义 :(2)定义的说明:1.数量积的定义正0负2.数量积的性质3.性质探究 问题4: 我们学过了实数乘法的哪些运算律?
a,b为实数①交换律:ab=ba
②结合律:(ab)c=a(bc)
③分配律:(a+b)c=ac+bc
④ ac=bc且c不为0,则a=b4.运算律探究对于向量还成立吗?自主探究,合作交流3、数量积的运算律 已知向量 和实数λ,则:课后学生独立证明运算律5.应用与提高6.小结与作业作业: 课本P108习题2.4A组1、2、3。
已知 与 都是非零向量,且 与
垂直, 与 垂直,求 与 的夹角。7.拓展与提高谢谢大家!
再见!例题例1 已知|a|=5, |b|=4, a与b的夹角θ=120o,求a·b.练习P106作业:
课本P108习题2.4A组1、2、3。?练习:三、讲解范例:
例1 已知|a|=5, |b|=4, a与b的夹角θ=120o,求a·b.
例2 已知|a|=6, |b|=4, a与b的夹角为60o求(a+2b)·(a-3b).
例3 已知|a|=3, |b|=4, 且a与b不共线,k为何值时,
向量a+kb与a-kb互相垂直.
例4 判断正误,并简要说明理由.
①a·0=0;②0·a=0;③0-=④|a·b|=|a||b|;
⑤若a≠0,则对任一非零b有a·b≠0;
⑥a·b=0,则a与b中至少有一个为0;
⑦对任意向量a,b,с都有(a·b) ·c= a·(b ·c)
⑧a与b是两个单位向量,则a2=b2.小结:1.
2.可用来求向量的模3.投影作业:学习目标:
1.掌握平面向量的数量积及其几何意义;
2.掌握平面向量数量积的重要性质及运算律;
3.了解用平面向量的数量积可以处理有关长度、角度和垂直的问题; 4.掌握向量垂直的条件.$﹫·一、复习引入:1. 向量共线定理 2.平面向量基本定理 3.平面向量的坐标表示4.平面向量的坐标运算5.∥ (?)的条件 6.两个非零向量夹角的概念
(1) 两个向量的数量积是一个数量,其大小由两个向量的长度及夹角决定. 此点很重要定义理解注:
(1)两个向量的数量积与实数同向量的积的区别:
两个向量的数量积是一个实数,不是向量,符号
由cos?的符号所决定,而实数同向量的积是一个向量
. 1. 两个向量的数量积是一个实数,不是向量,符号
由cos?的符号所决定,而实数同向量的积是一个向量2.两个向量的数量积称为内积,写成a?b;今后要学到两个向量的外积a×b,
而a?b是两个向量的数量的积,书写时要严格区分.符号“· ”在向量运算中不是乘号,
既不能省略,也不能用“×”代替.(1)定义 :(2)定义的简单说明:1.数量积的定义 问题4:向量的数量积运算与线性(加减法、数乘)运算的结果有什么不同?影响数量积大小的因素有哪些?并完成下表:2.研究数量积的几何意义(1)给出向量投影的概念(2)问题6:数量积的几何意义是什么?(1)定义 :(2)定义的简单说明:2、明晰数量积的定义 问题5:向量的数量积运算与线性(加减法、数乘)运算的结果有什么不同?影响数量积大小的因素有哪些?并完成下表:返回2.平面向量数量积(内积)的定义:已知两个非零向量a与b,
它们的夹角是θ,则数量|a||b|cos?叫a与b的数量积,
记作a?b,即有a?b = |a||b|cos?,
(0≤θ≤π).并规定0与任何向量的数量积为0.?探究:1.两个向量的数量积与同实数积有什么区别?2.两个向量的数量积与实数同向量的积有什么区别?返回(1)两个向量的数量积是一个实数,不是向量,符号由cos?的符号所决定.
(2)两个向量的数量积称为内积,写成a?b;今后要学到两个向量的外积a×b,
而a?b是两个向量的数量的积,书写时要严格区分.符号“· ”在向量运算中不是乘号,
既不能省略,也不能用“×”代替.
(3)在实数中,若a?0,且a?b=0,则b=0;但是在数量积中,若a?0,且a?b=0,
不能推出b=0.因为其中cos?有可能为0.
(4)已知实数a、b、c(b?0),则ab=bc ? a=c.但是a?b = b?c不能
得到 a=c
如右图:a?b = |a||b|cos? = |b||OA|,b?c = |b||c|cos? = |b||OA|
? a?b = b?c 但a ? c
(5)在实数中,有(a?b)c = a(b?c),但是(a?b)c ? a(b?c)
显然,这是因为左端是与c共线的向量,而右端是与a共线的向量,
而向量a与c不一定共线.两个向量的数量积与同实数积的区别两个向量的数量积与实数同向量的积的区别 两个向量的数量积是一个实数,不是向量,符号
由cos?的符号所决定,而实数同向量的积是一个向量 回忆两个向量的夹角返回概念:作3.“投影”的图
定义:|b|cos?叫做向量b在a方向上的投影.
投影也是一个数量,不是向量;当?为锐角时投影为正值;
当?为钝角时投影为负值;当?为直角时投影为0;当? = 0?时投影
为 |b|;当? = 180?时投影为 ?|b|.
返回4.向量的数量积的几何意义:
数量积a?b等于a的长度与b在a方向上投影|b|cos?的乘积.
5.两个向量的数量积的性质:
设a、b为两个非零向量,e是与b同向的单位向量.1? e?a = a?e =|a|cos?
2? a?b ? a?b = 0
3? 当a与b同向时,a?b = |a||b|;当a与b反向时,a?b = ?|a||b|.
特别的a?a = |a|2或4? cos? =5? |a?b| ≤ |a||b| 4. 向量的投影的概念 注意:当 q 为锐角时,投影是正值:当 q 为钝角时,投影是负值;当 q = 90° 时, 投影是 0 . 当q = 0o 时,投影为 ;
当q = 180°时,投影为 . (2) 两个向量数量积的几何意义思考并回答下列问题1.向量夹角的取值范围?
2.影响数量积大小的因素有哪些?
3.向量的数量积运算与线性(加减法、数乘)
运算的结果有什么区别?
4. 向量投影的概念?投影的取值范围?
5.平面向量的几何意义?
