15.1 轴对称图形(2)课时作业
图片预览




文档简介
16.1 轴对称图形(2)课时作业
姓名:__________班级:__________考号:__________
、选择题(本大题共7小题,每小题5分,共35分)
1.在直角坐标系内,点P(﹣3,5)关于x轴的对称点P1的坐标为( )
A. (3,﹣5) B. (3,5) C. (﹣3,5) D. (﹣3,﹣5)
2.在平面直角坐标系中,点A(m,2)与点B(3,n)关于y轴对称,则( )
A.m=3,n=2 B.m=﹣3,n=2 C.m=2,n=3 D.m=﹣2,n=﹣3
3.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(﹣1,0)表示,右下角方子的位置用(0,﹣1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.他放的位置是( )
A.(﹣2,1) B.(﹣1,1) C.(1,﹣2) D.(﹣1,﹣2)
4.在平面直角坐标系中,将点A(﹣1,﹣2)向右平移3个单位长度得到点B,则点B关于x轴的对称点B′的坐标为( )
A.(﹣3,﹣2) B.(2,2) C.(﹣2,2) D.(2,﹣2)
5.已知A.B两点的坐标分别是(-2,3)和(2,3),则下面四个结论中正确的有 ( ).
①A.B关于x轴对称;②A.B关于y轴对称;③A.B不轴对称;④A.B之间的距离为4.
A.1个 B.2个 C.3个 D.4个
6.在平面直角坐标系中,将点A(﹣1,﹣2)向右平移3个单位长度得到点B,则点B关于x轴的对称点B′的坐标为( )
A.(﹣3,﹣2) B.(2,2) C.(﹣2,2) D.(2,﹣2)
7.如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )
A.(—2012,2) B.(一2012,一2) C. (—2013,—2) D. (—2013,2)
、填空题(本大题共6小题,每小题5分,共30分)
8.在平面直角坐标系中,点P(4,2)关于直线x=1的对称点的坐标是 .
9.在平面直角坐标系中,点M(a,b)与点N(3,﹣1)关于x轴对称,则a+b的值是 .
10.已知A.E两点的坐标分别是(2,﹣3)和(2,3),则下面结论:(1)A.E两点关于x轴对称;(2)A.E两点关于y轴对称;(3)A.E两点关于原点对称,其中正确的是__________(填序号)
11.△ABC的三个顶点的坐标分别为A(4,4),B(1,1),C(6,2),△ABC关于x轴对称的图形为△A′B′C′,那么A′、B′、C′的坐标分别为__________________________.
12.已知点A(a﹣1,5)和点B(2,b﹣1)关于x轴对称,则(a+b)2013的值为 .
13.在平面直角坐标系中,点A的坐标是(4,﹣6),作点A关于x轴的对称点,得到点A′,再作点A′关于y轴的对称点,得到点A″,则点A″的坐标是 .
、解答题(本大题共5小题,共35分)
14.如图,△ABC,求顶点A.B、C关于y轴对称点的坐标。
15.如图,正方形ABCD的中心为O,AD∥x轴,CD∥y轴,若点A的坐标为(1,1),说出点B、C、D的坐标.(根据什么?)
16.在直角坐标系中,已知A(1,5),B(﹣4,﹣2),C(1,0)三点.
(1)点A关于x轴的对称的A′的坐标为 ;点B关于y轴的对称点B′的坐标为 ;点C关于y轴的对称点C′的坐标为 .
(2)求(1)中的△A′B′C′的面积.
17.如图,方格子的边长为1,△ABC的顶点在格点上.
(1)画出△ABC关于直线l对称的△A1B1C1;
(2)求△ABC的面积.
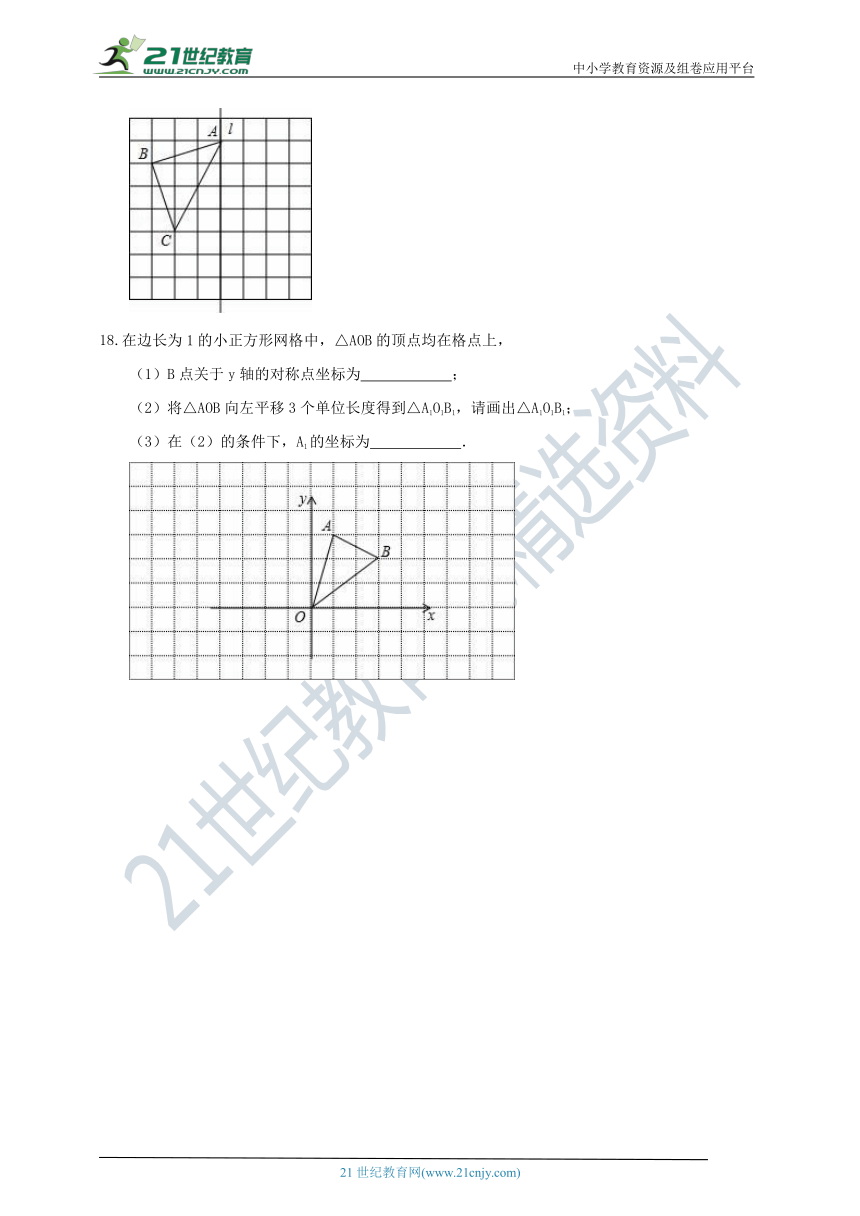
18.在边长为1的小正方形网格中,△AOB的顶点均在格点上,
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,A1的坐标为 .
答案解析
、选择题
1.【考点】 关于x轴、y轴对称的点的坐标.
【分析】 直接利用关于x轴对称点的性质得出P1点坐标即可.
解:∵点P(﹣3,5)关于x轴的对称点为P1,
∴P1的坐标为:(﹣3,﹣5).
故选:D.
【点评】 此题主要考查了关于x轴对称点的性质,正确把握横纵坐标的关系是解题关键.
2.【考点】关于x轴、y轴对称的点的坐标
【分析】直接利用关于y轴对称点的性质得出答案.
解:∵点A(m,2)与点B(3,n)关于y轴对称,
∴m=﹣3,n=2.
故选:B.
【点评】此题主要考查了关于y轴对称点的性质,正确记忆横纵坐标的关系是解题关键.
3.【考点】坐标与图形变化﹣对称;坐标确定位置.
【分析】首先确定x轴、y轴的位置,然后根据轴对称图形的定义判断.
解:棋盘中心方子的位置用(﹣1,0)表示,则这点所在的横线是x轴,右下角方子的位置用(0,﹣1),则这点所在的纵线是y轴,则当放的位置是(﹣1,1)时构成轴对称图形.
故选B.
【点评】本题考查了轴对称图形和坐标位置的确定,正确确定x轴、y轴的位置是关键.
4.【考点】关于x轴、y轴对称的点的坐标;坐标与图形变化﹣平移.
【分析】首先根据横坐标右移加,左移减可得B点坐标,然后再关于x轴对称点的坐标特点:横坐标不变,纵坐标符号改变可得答案.
解:点A(﹣1,﹣2)向右平移3个单位长度得到的B的坐标为(﹣1+3,﹣2),即(2,﹣2),
则点B关于x轴的对称点B′的坐标是(2,2),
故选:B.
【点评】 此题主要考查了坐标与图形变化-平移,以及关于x轴对称点的坐标,关键是掌握点的坐标变化规律.
5.【考点】关于x轴、y轴对称的点的坐标
【分析】根据平面内点对称的特点求解
解:①A.B关于x轴对称,错误;
②A,B关于y轴对称,正确;
③A.B关于原点对称,错误;
④若A,B之间的距离为4,正确;
正确的只有②④,
故选B。
【点评】此题主要考查了关于x轴对称点的性质以及两点的距离,正确把握横纵坐标的关系是解题关键.
6.【考点】坐标与图形变化﹣平移,关于x轴对称点的坐标
【分析】首先根据横坐标右移加,左移减可得B点坐标,然后再根据关于x轴对称点的坐标特点:横坐标不变,纵坐标符号改变可得答案.
解:点A(﹣1,﹣2)向右平移3个单位长度得到的B的坐标为(﹣1+3,﹣2),即(2,﹣2),
则点B关于x轴的对称点B′的坐标是(2,2),
故选:B.
【点评】此题主要考查了坐标与图形变化﹣平移,以及关于x轴对称点的坐标,关键是掌握点的坐标变化规律.
7.【考点】坐标与图形变化-对称;坐标与图形变化-平移.
【分析】首先求出正方形对角线交点坐标分别是(2,2),然后根据题意求得第1次、2次、3次变换后的点M的对应点的坐标,即可得规律.
解:∵正方形ABCD,点A(1,3)、B(1,1)、C(3,1).∴M的坐标变为(2,2) ∴根据题意得:第1次变换后的点M的对应点的坐标为(2-1,-2),即(1,-2),
第2次变换后的点M的对应点的坐标为:(2-2,2),即(0,2),
第3次变换后的点M的对应点的坐标为(2-3,-2),即(-1,-2),
第2014次变换后的点M的对应点的为坐标为(2-2014, 2),即(-2012, 2)
故答案为A.
【点评】此题考查了对称与平移的性质.此题难度较大,属于规律性题目,注意得到规律:第n次变换后的点M的对应点的坐标为:当n为奇数时为(2-n,-2),当n为偶数时为(2-n,2)是解此题的关键.
、填空题
8.【考点】坐标与图形变化﹣对称
【分析】先求出点P到直线x=1的距离,再根据对称性求出对称点P′到直线x=1的距离,从而得到点P′的横坐标,即可得解.
解:∵点P(4,2),
∴点P到直线x=1的距离为4﹣1=3,∴点P关于直线x=1的对称点P′到直线x=1的距离为3,
∴点P′的横坐标为1﹣3=﹣2,
∴对称点P′的坐标为(﹣2,2).
故答案为:(﹣2,2).
【点评】本题考查了坐标与图形变化﹣对称,根据轴对称性求出对称点到直线x=1的距离,从而得到横坐标是解题的关键,作出图形更形象直观.
9.【考点】关于x轴、y轴对称的点的坐标
【分析】直接利用关于x轴对称点的性质得出a,b的值,进而得出答案.
解:∵点M(a,b)与点N(3,﹣1)关于x轴对称,
∴a=3,b=1,
则a+b的值是:4.
故答案为:4.
【点评】此题主要考查了关于x轴对称点的性质,正确掌握横纵坐标的关系是解题关键.
10.【考点】关于原点对称的点的坐标;关于x轴、y轴对称的点的坐标.
【分析】根据关于x轴对称的点的点的横坐标相同,纵坐标互为相反数,可得答案.
解:由A.E两点的坐标分别是(2,﹣3)和(2,3),得
A.E两点关于x轴对称,
故答案为:(1).
【点评】本题考查了关于原点对称的点的坐标,关于x轴对称的点的点的横坐标相同,纵坐标互为相反数.
11.【考点】 关于x轴、y轴对称的点的坐标.
【分析】 利用关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数,即点P(x,y)关于x轴的对称点P′的坐标是(x,﹣y),进而得出答案.
解:∵△ABC的三个顶点的坐标分别为A(4,4),B(1,1),C(6,2),△ABC关于x轴对称的图形为△A′B′C′,
∴A′、B′、C′的坐标分别为(4,﹣4),(1,﹣1),(6,﹣2).
故答案为:(4,﹣4),(1,﹣1),(6,﹣2).
【点评】此题主要考查了关于x轴对称点的性质,正确把握横纵坐标的关系是解题关键.
12.【考点】关于x轴、y轴对称的点的坐标.
【分析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得a、b的值,然后再代入求值即可.
解:∵点A(a﹣1,5)和点B(2,b﹣1)关于x轴对称,
∴a﹣1=2,b﹣1=﹣5,
解得:a=3,b=﹣4,
∴(a+b)2013=(3﹣4)2013=﹣1,
故答案为:﹣1.
【点评】此题主要考查了关于x轴对称点的坐标特点,关键是掌握点的坐标的变化规律.
13.【考点】关于x轴、y轴对称的点的坐标
【分析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变可得答案.
解:∵点A的坐标是(4,﹣6),
∴点A关于x轴的对称点A′(4,6),
∴点A′关于y轴的对称点A″(﹣4,6),
故答案为:(﹣4,6).
【点评】此题主要考查了关于x、y轴对称的点的坐标,关键是掌握点的坐标的变化规律.
、解答题
14.【考点】关于x轴、y轴对称的点的坐标
【分析】要确定点A.B、C关于y轴对称点的坐标,首先要写出A.B、C点的坐标,然后根据关于y轴对称点之间的坐标规律求对称点的坐标。
解:A.B、C点的坐标分别是A(-3,2),B(-4,-2),C(-2,-3),
∵点(x,y)关于y轴对称点的坐标为(-x,y),
∴点A.B、C关于y轴对称点的坐标分别是A′(3,2),B′(4,-2),C′(2,-3).
【点评】本题考查了关于x轴、y轴对称的点的坐标,注意掌握轴对称的性质,关于x轴、y轴对称的点的坐标特点.
15.【考点】关于x轴、y轴对称的点的坐标
【分析】根据关于x轴、y轴对称的点的坐标进行求解。
解:点A与B关于x轴对称,点A与D关于y轴对称,点C与B关于y轴对称,点D与C关于x轴对称。故B(1,-1),C(-1,-1),D(-1,1)
【点睛】本题考查了关于x轴、y轴对称的点的坐标,熟记关于x轴、y轴对称的点的坐标特点是关键
16.【考点】关于x轴、y轴对称的点的坐标
【分析】关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数;关于原点对称的点,横坐标与纵坐标都互为相反数.
解:(1)点A关于x轴的对称的A′的坐标为 (1,﹣5);点B关于y轴的对称点B′的坐标为 (4,﹣2);点C关于y轴的对称点C′的坐标为 (﹣1,0).
(2)求(1)中的△A′B′C′的面积,
S△A′B′B′=S△ABC=AC?|xB|=×5×|﹣4|=10,
故答案为:(1,﹣5),(4,﹣2),(﹣1,0).
【点评】本题考查了关于原点对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数;关于原点对称的点,横坐标与纵坐标都互为相反数.
17.【考点】作图-轴对称变换.
【分析】(1)分别找出A.B、C三点的对称点,再顺次连接即可;
(2)利用长方形的面积减去周围多余三角形的面积即可得到△ABC的面积.
解:(1)如图所示:
(2)△ABC的面积:
3×4﹣﹣﹣
=12﹣3﹣4
=5.
【点评】此题主要考查了作图﹣﹣轴对称变换,关键是找出对称点的位置.
18.【考点】作图-平移变换;关于x轴、y轴对称的点的坐标.
【分析】(1)根据关于y轴对称的点的横坐标互为相反数,纵坐标相等解答;
(2)根据网格结构找出点A.O、B向左平移后的对应点A1、O1、B1的位置,然后顺次连接即可;
(3)根据平面直角坐标系写出坐标即可.
解:(1)B点关于y轴的对称点坐标为(﹣3,2);
(2)△A1O1B1如图所示;
(3)A1的坐标为(﹣2,3).
故答案为:(1)(﹣3,2);(3)(﹣2,3).
【点评】本题考查了利用平移变换作图,关于y轴对称点的坐标,熟练掌握网格结构准确找出对应点的位置是解题的关键.
姓名:__________班级:__________考号:__________
、选择题(本大题共7小题,每小题5分,共35分)
1.在直角坐标系内,点P(﹣3,5)关于x轴的对称点P1的坐标为( )
A. (3,﹣5) B. (3,5) C. (﹣3,5) D. (﹣3,﹣5)
2.在平面直角坐标系中,点A(m,2)与点B(3,n)关于y轴对称,则( )
A.m=3,n=2 B.m=﹣3,n=2 C.m=2,n=3 D.m=﹣2,n=﹣3
3.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(﹣1,0)表示,右下角方子的位置用(0,﹣1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.他放的位置是( )
A.(﹣2,1) B.(﹣1,1) C.(1,﹣2) D.(﹣1,﹣2)
4.在平面直角坐标系中,将点A(﹣1,﹣2)向右平移3个单位长度得到点B,则点B关于x轴的对称点B′的坐标为( )
A.(﹣3,﹣2) B.(2,2) C.(﹣2,2) D.(2,﹣2)
5.已知A.B两点的坐标分别是(-2,3)和(2,3),则下面四个结论中正确的有 ( ).
①A.B关于x轴对称;②A.B关于y轴对称;③A.B不轴对称;④A.B之间的距离为4.
A.1个 B.2个 C.3个 D.4个
6.在平面直角坐标系中,将点A(﹣1,﹣2)向右平移3个单位长度得到点B,则点B关于x轴的对称点B′的坐标为( )
A.(﹣3,﹣2) B.(2,2) C.(﹣2,2) D.(2,﹣2)
7.如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )
A.(—2012,2) B.(一2012,一2) C. (—2013,—2) D. (—2013,2)
、填空题(本大题共6小题,每小题5分,共30分)
8.在平面直角坐标系中,点P(4,2)关于直线x=1的对称点的坐标是 .
9.在平面直角坐标系中,点M(a,b)与点N(3,﹣1)关于x轴对称,则a+b的值是 .
10.已知A.E两点的坐标分别是(2,﹣3)和(2,3),则下面结论:(1)A.E两点关于x轴对称;(2)A.E两点关于y轴对称;(3)A.E两点关于原点对称,其中正确的是__________(填序号)
11.△ABC的三个顶点的坐标分别为A(4,4),B(1,1),C(6,2),△ABC关于x轴对称的图形为△A′B′C′,那么A′、B′、C′的坐标分别为__________________________.
12.已知点A(a﹣1,5)和点B(2,b﹣1)关于x轴对称,则(a+b)2013的值为 .
13.在平面直角坐标系中,点A的坐标是(4,﹣6),作点A关于x轴的对称点,得到点A′,再作点A′关于y轴的对称点,得到点A″,则点A″的坐标是 .
、解答题(本大题共5小题,共35分)
14.如图,△ABC,求顶点A.B、C关于y轴对称点的坐标。
15.如图,正方形ABCD的中心为O,AD∥x轴,CD∥y轴,若点A的坐标为(1,1),说出点B、C、D的坐标.(根据什么?)
16.在直角坐标系中,已知A(1,5),B(﹣4,﹣2),C(1,0)三点.
(1)点A关于x轴的对称的A′的坐标为 ;点B关于y轴的对称点B′的坐标为 ;点C关于y轴的对称点C′的坐标为 .
(2)求(1)中的△A′B′C′的面积.
17.如图,方格子的边长为1,△ABC的顶点在格点上.
(1)画出△ABC关于直线l对称的△A1B1C1;
(2)求△ABC的面积.
18.在边长为1的小正方形网格中,△AOB的顶点均在格点上,
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,A1的坐标为 .
答案解析
、选择题
1.【考点】 关于x轴、y轴对称的点的坐标.
【分析】 直接利用关于x轴对称点的性质得出P1点坐标即可.
解:∵点P(﹣3,5)关于x轴的对称点为P1,
∴P1的坐标为:(﹣3,﹣5).
故选:D.
【点评】 此题主要考查了关于x轴对称点的性质,正确把握横纵坐标的关系是解题关键.
2.【考点】关于x轴、y轴对称的点的坐标
【分析】直接利用关于y轴对称点的性质得出答案.
解:∵点A(m,2)与点B(3,n)关于y轴对称,
∴m=﹣3,n=2.
故选:B.
【点评】此题主要考查了关于y轴对称点的性质,正确记忆横纵坐标的关系是解题关键.
3.【考点】坐标与图形变化﹣对称;坐标确定位置.
【分析】首先确定x轴、y轴的位置,然后根据轴对称图形的定义判断.
解:棋盘中心方子的位置用(﹣1,0)表示,则这点所在的横线是x轴,右下角方子的位置用(0,﹣1),则这点所在的纵线是y轴,则当放的位置是(﹣1,1)时构成轴对称图形.
故选B.
【点评】本题考查了轴对称图形和坐标位置的确定,正确确定x轴、y轴的位置是关键.
4.【考点】关于x轴、y轴对称的点的坐标;坐标与图形变化﹣平移.
【分析】首先根据横坐标右移加,左移减可得B点坐标,然后再关于x轴对称点的坐标特点:横坐标不变,纵坐标符号改变可得答案.
解:点A(﹣1,﹣2)向右平移3个单位长度得到的B的坐标为(﹣1+3,﹣2),即(2,﹣2),
则点B关于x轴的对称点B′的坐标是(2,2),
故选:B.
【点评】 此题主要考查了坐标与图形变化-平移,以及关于x轴对称点的坐标,关键是掌握点的坐标变化规律.
5.【考点】关于x轴、y轴对称的点的坐标
【分析】根据平面内点对称的特点求解
解:①A.B关于x轴对称,错误;
②A,B关于y轴对称,正确;
③A.B关于原点对称,错误;
④若A,B之间的距离为4,正确;
正确的只有②④,
故选B。
【点评】此题主要考查了关于x轴对称点的性质以及两点的距离,正确把握横纵坐标的关系是解题关键.
6.【考点】坐标与图形变化﹣平移,关于x轴对称点的坐标
【分析】首先根据横坐标右移加,左移减可得B点坐标,然后再根据关于x轴对称点的坐标特点:横坐标不变,纵坐标符号改变可得答案.
解:点A(﹣1,﹣2)向右平移3个单位长度得到的B的坐标为(﹣1+3,﹣2),即(2,﹣2),
则点B关于x轴的对称点B′的坐标是(2,2),
故选:B.
【点评】此题主要考查了坐标与图形变化﹣平移,以及关于x轴对称点的坐标,关键是掌握点的坐标变化规律.
7.【考点】坐标与图形变化-对称;坐标与图形变化-平移.
【分析】首先求出正方形对角线交点坐标分别是(2,2),然后根据题意求得第1次、2次、3次变换后的点M的对应点的坐标,即可得规律.
解:∵正方形ABCD,点A(1,3)、B(1,1)、C(3,1).∴M的坐标变为(2,2) ∴根据题意得:第1次变换后的点M的对应点的坐标为(2-1,-2),即(1,-2),
第2次变换后的点M的对应点的坐标为:(2-2,2),即(0,2),
第3次变换后的点M的对应点的坐标为(2-3,-2),即(-1,-2),
第2014次变换后的点M的对应点的为坐标为(2-2014, 2),即(-2012, 2)
故答案为A.
【点评】此题考查了对称与平移的性质.此题难度较大,属于规律性题目,注意得到规律:第n次变换后的点M的对应点的坐标为:当n为奇数时为(2-n,-2),当n为偶数时为(2-n,2)是解此题的关键.
、填空题
8.【考点】坐标与图形变化﹣对称
【分析】先求出点P到直线x=1的距离,再根据对称性求出对称点P′到直线x=1的距离,从而得到点P′的横坐标,即可得解.
解:∵点P(4,2),
∴点P到直线x=1的距离为4﹣1=3,∴点P关于直线x=1的对称点P′到直线x=1的距离为3,
∴点P′的横坐标为1﹣3=﹣2,
∴对称点P′的坐标为(﹣2,2).
故答案为:(﹣2,2).
【点评】本题考查了坐标与图形变化﹣对称,根据轴对称性求出对称点到直线x=1的距离,从而得到横坐标是解题的关键,作出图形更形象直观.
9.【考点】关于x轴、y轴对称的点的坐标
【分析】直接利用关于x轴对称点的性质得出a,b的值,进而得出答案.
解:∵点M(a,b)与点N(3,﹣1)关于x轴对称,
∴a=3,b=1,
则a+b的值是:4.
故答案为:4.
【点评】此题主要考查了关于x轴对称点的性质,正确掌握横纵坐标的关系是解题关键.
10.【考点】关于原点对称的点的坐标;关于x轴、y轴对称的点的坐标.
【分析】根据关于x轴对称的点的点的横坐标相同,纵坐标互为相反数,可得答案.
解:由A.E两点的坐标分别是(2,﹣3)和(2,3),得
A.E两点关于x轴对称,
故答案为:(1).
【点评】本题考查了关于原点对称的点的坐标,关于x轴对称的点的点的横坐标相同,纵坐标互为相反数.
11.【考点】 关于x轴、y轴对称的点的坐标.
【分析】 利用关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数,即点P(x,y)关于x轴的对称点P′的坐标是(x,﹣y),进而得出答案.
解:∵△ABC的三个顶点的坐标分别为A(4,4),B(1,1),C(6,2),△ABC关于x轴对称的图形为△A′B′C′,
∴A′、B′、C′的坐标分别为(4,﹣4),(1,﹣1),(6,﹣2).
故答案为:(4,﹣4),(1,﹣1),(6,﹣2).
【点评】此题主要考查了关于x轴对称点的性质,正确把握横纵坐标的关系是解题关键.
12.【考点】关于x轴、y轴对称的点的坐标.
【分析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得a、b的值,然后再代入求值即可.
解:∵点A(a﹣1,5)和点B(2,b﹣1)关于x轴对称,
∴a﹣1=2,b﹣1=﹣5,
解得:a=3,b=﹣4,
∴(a+b)2013=(3﹣4)2013=﹣1,
故答案为:﹣1.
【点评】此题主要考查了关于x轴对称点的坐标特点,关键是掌握点的坐标的变化规律.
13.【考点】关于x轴、y轴对称的点的坐标
【分析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变可得答案.
解:∵点A的坐标是(4,﹣6),
∴点A关于x轴的对称点A′(4,6),
∴点A′关于y轴的对称点A″(﹣4,6),
故答案为:(﹣4,6).
【点评】此题主要考查了关于x、y轴对称的点的坐标,关键是掌握点的坐标的变化规律.
、解答题
14.【考点】关于x轴、y轴对称的点的坐标
【分析】要确定点A.B、C关于y轴对称点的坐标,首先要写出A.B、C点的坐标,然后根据关于y轴对称点之间的坐标规律求对称点的坐标。
解:A.B、C点的坐标分别是A(-3,2),B(-4,-2),C(-2,-3),
∵点(x,y)关于y轴对称点的坐标为(-x,y),
∴点A.B、C关于y轴对称点的坐标分别是A′(3,2),B′(4,-2),C′(2,-3).
【点评】本题考查了关于x轴、y轴对称的点的坐标,注意掌握轴对称的性质,关于x轴、y轴对称的点的坐标特点.
15.【考点】关于x轴、y轴对称的点的坐标
【分析】根据关于x轴、y轴对称的点的坐标进行求解。
解:点A与B关于x轴对称,点A与D关于y轴对称,点C与B关于y轴对称,点D与C关于x轴对称。故B(1,-1),C(-1,-1),D(-1,1)
【点睛】本题考查了关于x轴、y轴对称的点的坐标,熟记关于x轴、y轴对称的点的坐标特点是关键
16.【考点】关于x轴、y轴对称的点的坐标
【分析】关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数;关于原点对称的点,横坐标与纵坐标都互为相反数.
解:(1)点A关于x轴的对称的A′的坐标为 (1,﹣5);点B关于y轴的对称点B′的坐标为 (4,﹣2);点C关于y轴的对称点C′的坐标为 (﹣1,0).
(2)求(1)中的△A′B′C′的面积,
S△A′B′B′=S△ABC=AC?|xB|=×5×|﹣4|=10,
故答案为:(1,﹣5),(4,﹣2),(﹣1,0).
【点评】本题考查了关于原点对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数;关于原点对称的点,横坐标与纵坐标都互为相反数.
17.【考点】作图-轴对称变换.
【分析】(1)分别找出A.B、C三点的对称点,再顺次连接即可;
(2)利用长方形的面积减去周围多余三角形的面积即可得到△ABC的面积.
解:(1)如图所示:
(2)△ABC的面积:
3×4﹣﹣﹣
=12﹣3﹣4
=5.
【点评】此题主要考查了作图﹣﹣轴对称变换,关键是找出对称点的位置.
18.【考点】作图-平移变换;关于x轴、y轴对称的点的坐标.
【分析】(1)根据关于y轴对称的点的横坐标互为相反数,纵坐标相等解答;
(2)根据网格结构找出点A.O、B向左平移后的对应点A1、O1、B1的位置,然后顺次连接即可;
(3)根据平面直角坐标系写出坐标即可.
解:(1)B点关于y轴的对称点坐标为(﹣3,2);
(2)△A1O1B1如图所示;
(3)A1的坐标为(﹣2,3).
故答案为:(1)(﹣3,2);(3)(﹣2,3).
【点评】本题考查了利用平移变换作图,关于y轴对称点的坐标,熟练掌握网格结构准确找出对应点的位置是解题的关键.
