2.1.2 向量的加法 课件(19张PPT)
文档属性
| 名称 | 2.1.2 向量的加法 课件(19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 654.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-31 17:07:49 | ||
图片预览




文档简介
课件19张PPT。2.2.1向量加法运算
及其几何意义学习目标:(1)向量加法的定义
(2)运用加法的“三角形法则”和“平行四边形法则”
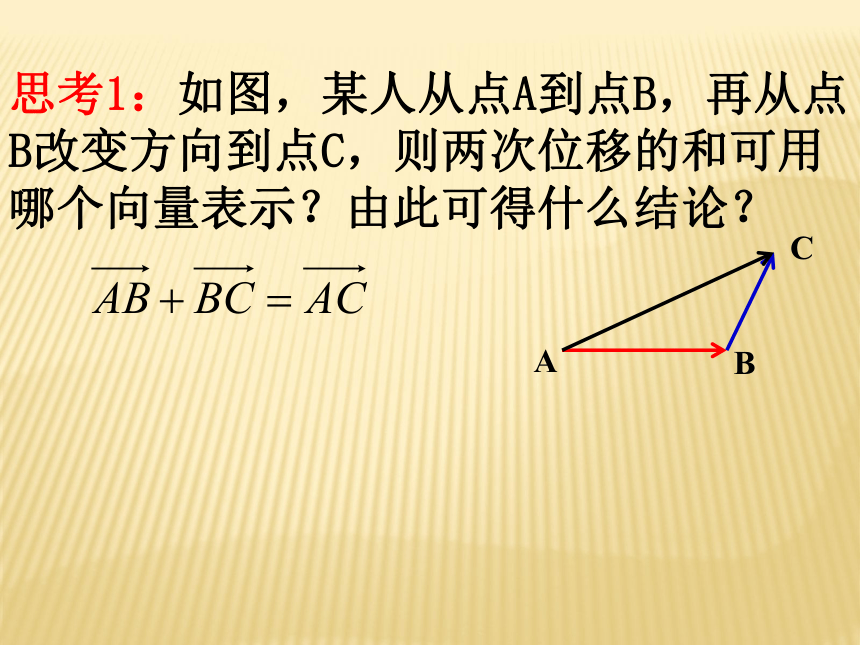
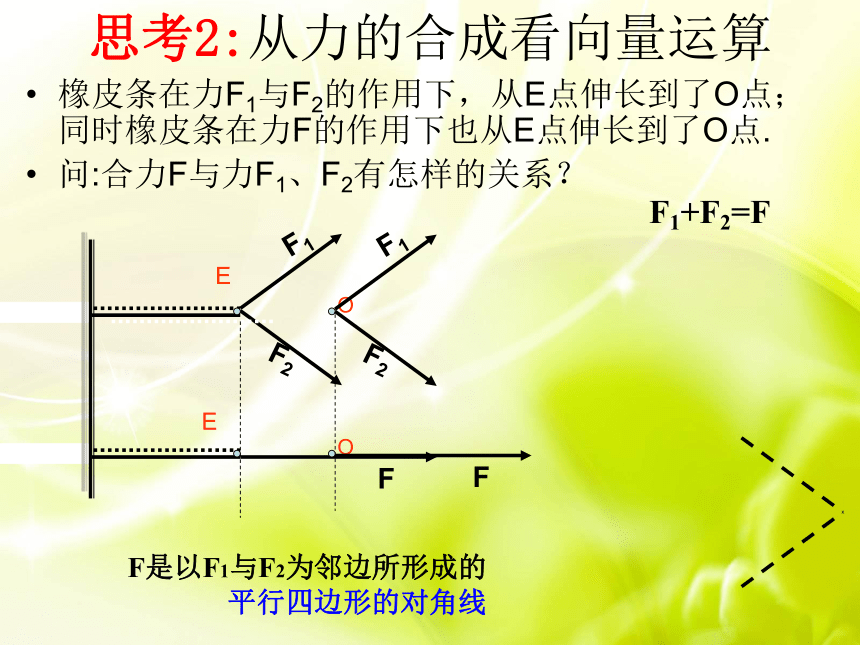
(3)掌握向量加法的交换律和结合律温故知新零01个单位相同或相反a∥b平行相等相同a=b 向量的关键特征是大小和方向说明:思考1:如图,某人从点A到点B,再从点B改变方向到点C,则两次位移的和可用哪个向量表示?由此可得什么结论?EOOEF1+F2=F思考2:从力的合成看向量运算橡皮条在力F1与F2的作用下,从E点伸长到了O点;同时橡皮条在力F的作用下也从E点伸长到了O点.
问:合力F与力F1、F2有怎样的关系?F是以F1与F2为邻边所形成的
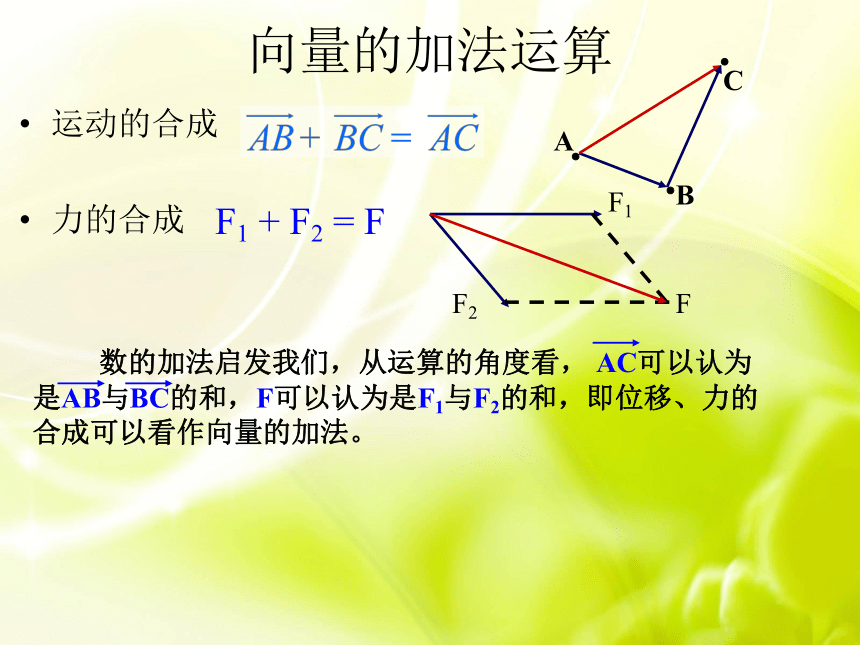
平行四边形的对角线ABC向量的加法运算运动的合成
力的合成向量加法的定义:我们把求两个向量 和的运算,叫做向量的加法, 叫做 的和.两个向量的和仍然是一个向量.一、向量加法的定义o·ABC力的合成可以看作向量加法的
平行四边形法则的物理模型CA·B二、向量加法二个法则位移的合成可以看作向量
加法三角形法则的物理模型bbaa向 量 加 法 向 量 加 法三 角 形 法 则:平行四边形法则:向量加法的定义尾首顺次相接
首指向尾为和起点相同,两边平行
同一起点,对角线为和起点相同,连对角口决:首尾相接,首尾连向量加法法则总结与拓展向量加法的三角形法则:
1.将向量平移使得它们首尾相连
2.和向量即是第一个向量的首指向第二个向量的尾
向量加法的平行四边形法则:
1.将向量平移到同一起点
2.和向量即以它们作为邻边平行四边形的共起点的对角线
首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.多边形法则:则作法1:在平面内任取一点O,例题讲解:o·ABo·ABC作法2:在平面内任取一点O,特例:共线向量方向相同方向相反思考???向 量 加 法向 量 加 法 三、向量加法的运算律:交换律:结合律:ADBCABCDABCDE1.根据图示填空:2.根据图示填空:
(1) + =____________
(2) + =____________向 量 加 法向 量 加 法3.化简小结1.一个定义--------2.两个法则--------3.两个运算律--------向量加法的定义三角形法则和平行四边形法则交换律和结合律作业课本91页第1题、第2题用向量方法证明对角线互相平分的四边形是平行四边形.思考题:?
及其几何意义学习目标:(1)向量加法的定义
(2)运用加法的“三角形法则”和“平行四边形法则”
(3)掌握向量加法的交换律和结合律温故知新零01个单位相同或相反a∥b平行相等相同a=b 向量的关键特征是大小和方向说明:思考1:如图,某人从点A到点B,再从点B改变方向到点C,则两次位移的和可用哪个向量表示?由此可得什么结论?EOOEF1+F2=F思考2:从力的合成看向量运算橡皮条在力F1与F2的作用下,从E点伸长到了O点;同时橡皮条在力F的作用下也从E点伸长到了O点.
问:合力F与力F1、F2有怎样的关系?F是以F1与F2为邻边所形成的
平行四边形的对角线ABC向量的加法运算运动的合成
力的合成向量加法的定义:我们把求两个向量 和的运算,叫做向量的加法, 叫做 的和.两个向量的和仍然是一个向量.一、向量加法的定义o·ABC力的合成可以看作向量加法的
平行四边形法则的物理模型CA·B二、向量加法二个法则位移的合成可以看作向量
加法三角形法则的物理模型bbaa向 量 加 法 向 量 加 法三 角 形 法 则:平行四边形法则:向量加法的定义尾首顺次相接
首指向尾为和起点相同,两边平行
同一起点,对角线为和起点相同,连对角口决:首尾相接,首尾连向量加法法则总结与拓展向量加法的三角形法则:
1.将向量平移使得它们首尾相连
2.和向量即是第一个向量的首指向第二个向量的尾
向量加法的平行四边形法则:
1.将向量平移到同一起点
2.和向量即以它们作为邻边平行四边形的共起点的对角线
首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.多边形法则:则作法1:在平面内任取一点O,例题讲解:o·ABo·ABC作法2:在平面内任取一点O,特例:共线向量方向相同方向相反思考???向 量 加 法向 量 加 法 三、向量加法的运算律:交换律:结合律:ADBCABCDABCDE1.根据图示填空:2.根据图示填空:
(1) + =____________
(2) + =____________向 量 加 法向 量 加 法3.化简小结1.一个定义--------2.两个法则--------3.两个运算律--------向量加法的定义三角形法则和平行四边形法则交换律和结合律作业课本91页第1题、第2题用向量方法证明对角线互相平分的四边形是平行四边形.思考题:?
