2.3.1 向量数量积的物理背景与定义 课件(23张PPT)
文档属性
| 名称 | 2.3.1 向量数量积的物理背景与定义 课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 310.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-31 17:11:15 | ||
图片预览




文档简介
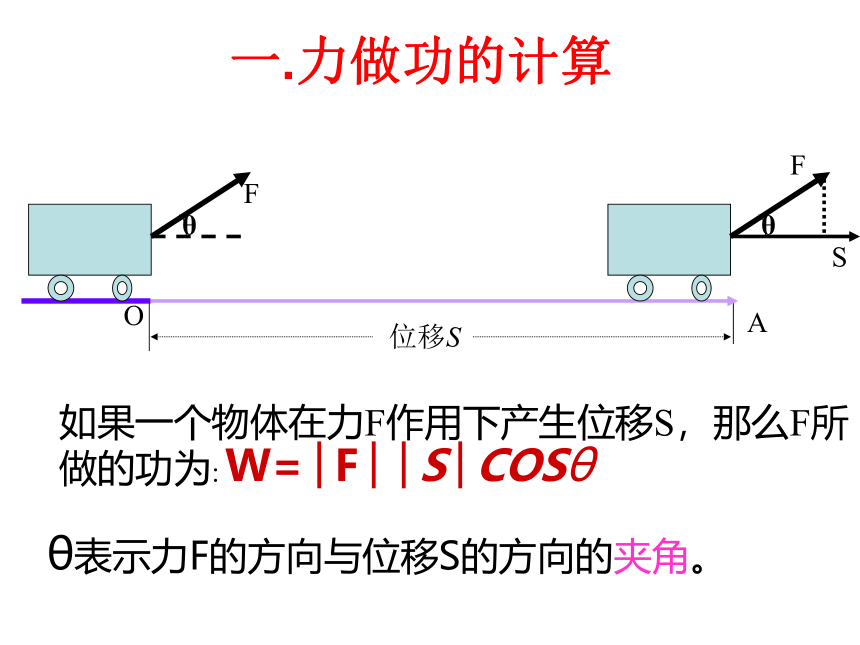
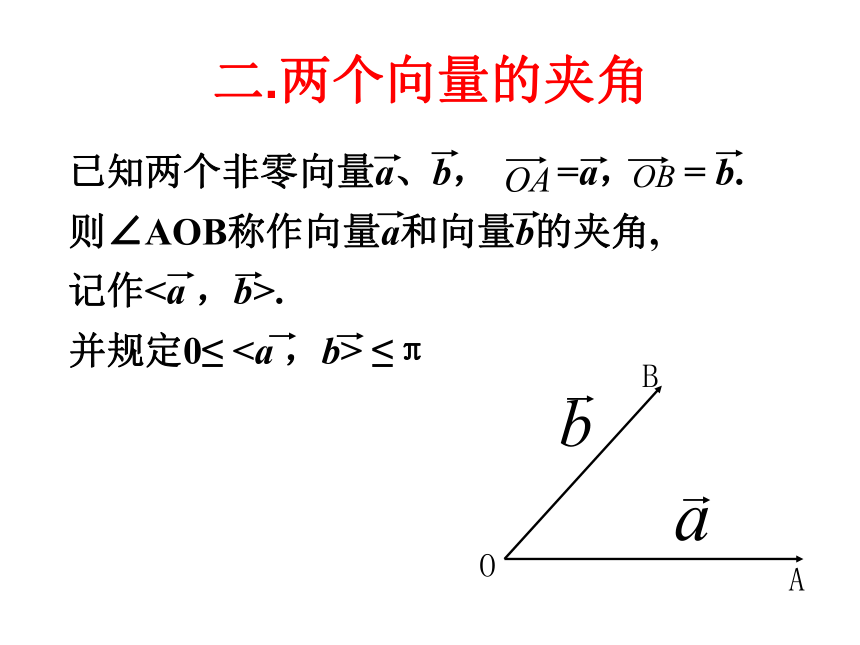
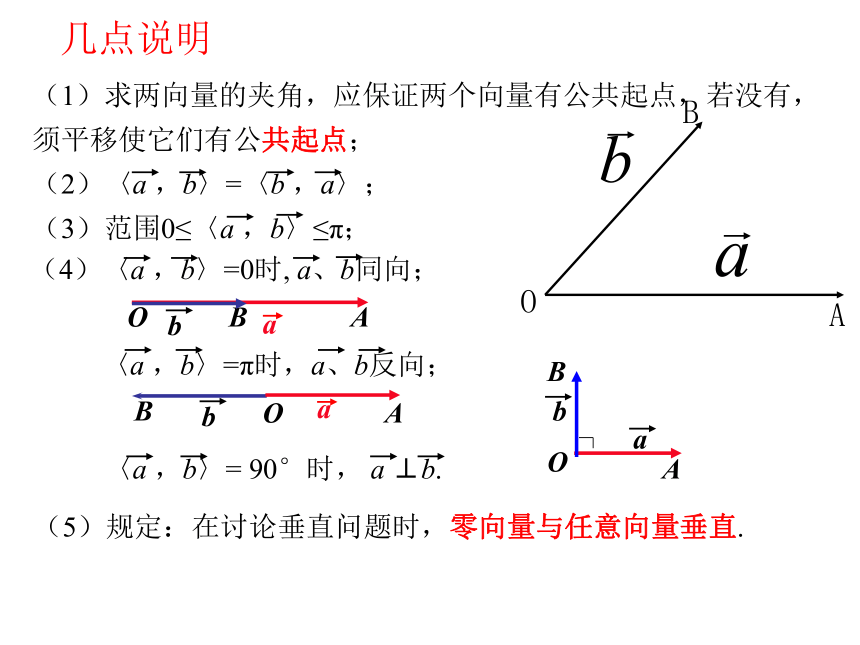
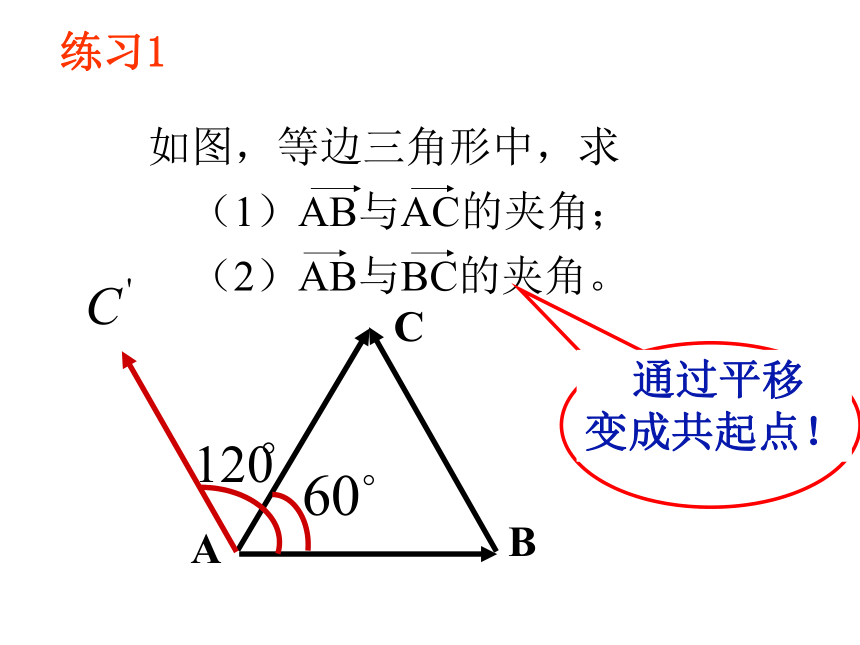
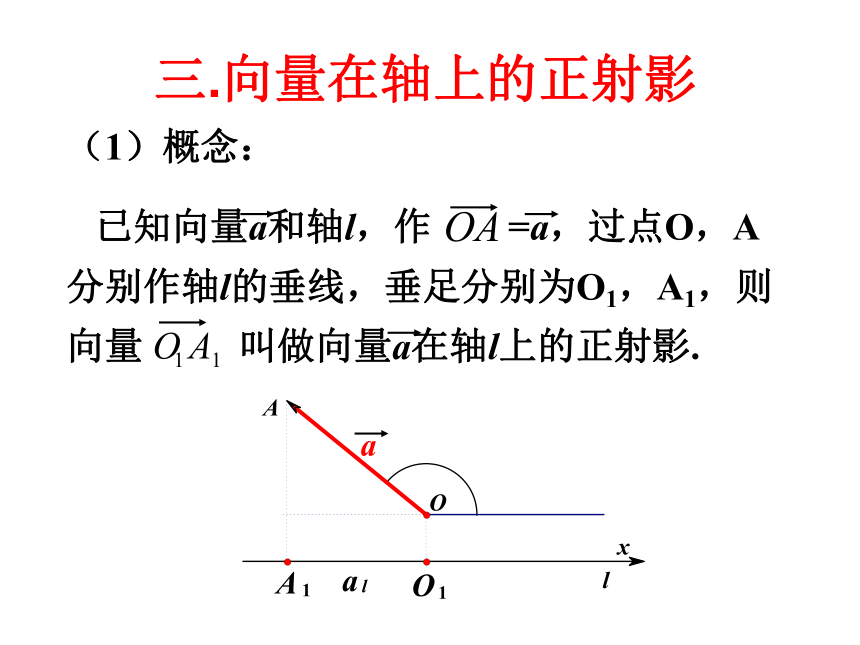
课件23张PPT。复习回顾x1 y2 - x2 y1=02.3.1 向量数量积的物 理背景与定义 如果一个物体在力F作用下产生位移S,那么F所做的功为:θ表示力F的方向与位移S的方向的夹角。W=│F││S│COSθ一.力做功的计算二.两个向量的夹角(1)求两向量的夹角,应保证两个向量有公共起点,若没有,须平移使它们有公共起点;(5)规定:在讨论垂直问题时,零向量与任意向量垂直.几点说明练习1三.向量在轴上的正射影 (2)正射影的数量: 1. a在轴l上的数量或在轴l方向上的数量是一个数量,不是向量.
2. 当?为锐角时,数量为正值;
3. 当?为钝角时,数量为负值;
4. 当?为直角时,数量为0;
5. 当? = 0?时,数量为 |a|;
6. 当? = 180?时,数量为 ?|a|. 几点说明xlO例1.已知轴l解:4cos600=2解:OA1=5COS600=5×( ?)=5/2-5/2四.向量的数量积(内积) 定义: 叫做向量a和b的数量积(或内积)
记作:a·b .
即 a·b = 几点说明θ为锐角时,
| b | cosθ>0θ为钝角时,
| b | cosθ<0θ为直角时,
| b | cosθ=04. a · b不能写成a×b ,a×b 表示向量的另一种运算.两个向量的数量积的性质:内积为零是判定两向量垂直的条件用于计算向量的模用于计算向量的夹角,
以及判断三角形的形状例2.已知|a|=5,|b|=4,=120°,求a·b.
解: a?b =|a|·|b|cos
=5×4×cos120°
= -10. 练习2在△ABC中, ,求,°练习3(1)A 锐角三角形C 钝角三角形D 不能确定B 直角三角形DCA 锐角三角形B 直角三角形C 钝角三角形D 不能确定判断下列命题是否正确(×)(×)(×)(×)练习4课堂小结1.两个向量的夹角2.向量在轴上的正射影 正射影的数量3.向量的数量积(内积) 4.两个向量的数量积的性质:
2. 当?为锐角时,数量为正值;
3. 当?为钝角时,数量为负值;
4. 当?为直角时,数量为0;
5. 当? = 0?时,数量为 |a|;
6. 当? = 180?时,数量为 ?|a|. 几点说明xlO例1.已知轴l解:4cos600=2解:OA1=5COS600=5×( ?)=5/2-5/2四.向量的数量积(内积) 定义: 叫做向量a和b的数量积(或内积)
记作:a·b .
即 a·b = 几点说明θ为锐角时,
| b | cosθ>0θ为钝角时,
| b | cosθ<0θ为直角时,
| b | cosθ=04. a · b不能写成a×b ,a×b 表示向量的另一种运算.两个向量的数量积的性质:内积为零是判定两向量垂直的条件用于计算向量的模用于计算向量的夹角,
以及判断三角形的形状例2.已知|a|=5,|b|=4,
解: a?b =|a|·|b|cos
=5×4×cos120°
= -10. 练习2在△ABC中, ,求,°练习3(1)A 锐角三角形C 钝角三角形D 不能确定B 直角三角形DCA 锐角三角形B 直角三角形C 钝角三角形D 不能确定判断下列命题是否正确(×)(×)(×)(×)练习4课堂小结1.两个向量的夹角2.向量在轴上的正射影 正射影的数量3.向量的数量积(内积) 4.两个向量的数量积的性质:
