3.1.1 两角和与差的余弦 课件(18张PPT)
文档属性
| 名称 | 3.1.1 两角和与差的余弦 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 649.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-31 00:00:00 | ||
图片预览


文档简介
课件18张PPT。3.1.1两角和与差的余弦公式 根据在第一章所学的知识可知这种猜想是错误的!
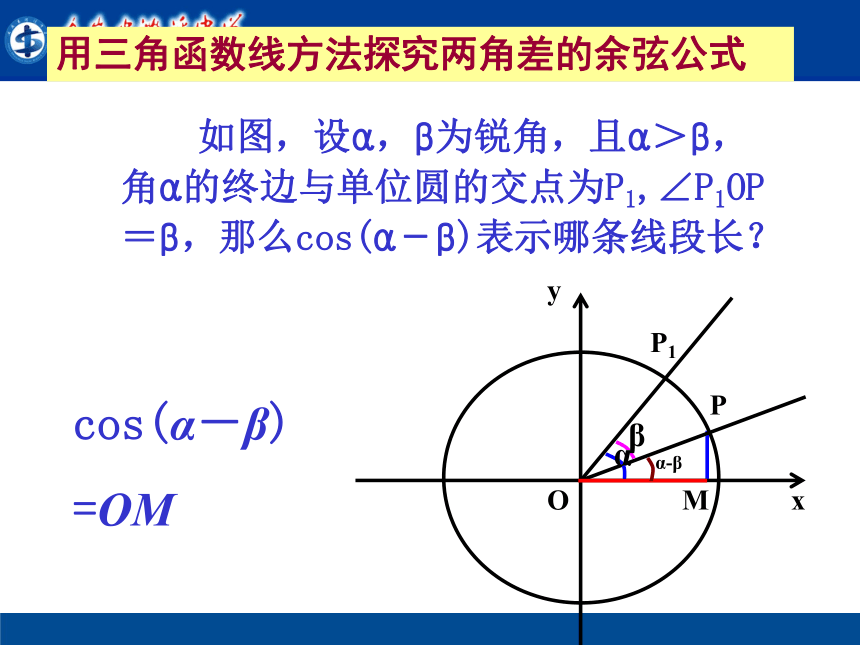
下面就一起探讨两角差的余弦公式α-β 如图,设α,β为锐角,且α>β,角α的终边与单位圆的交点为P1,∠P1OP=β,那么cos(α-β)表示哪条线段长?cos(α-β)
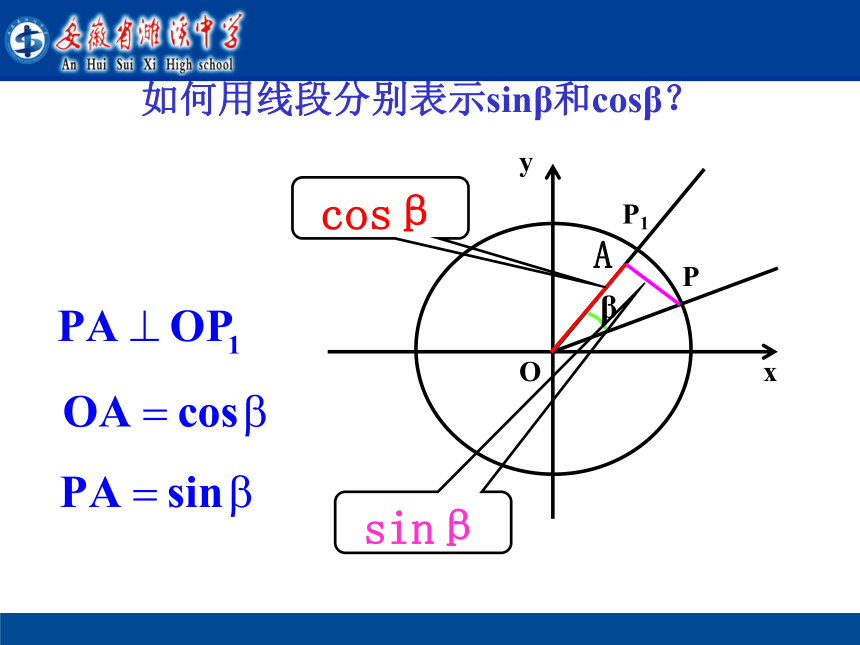
=OMαβ用三角函数线方法探究两角差的余弦公式 如何用线段分别表示sinβ和cosβ?sinβcosββOAcosα=cosαcosβ ,它表示哪条线段长?
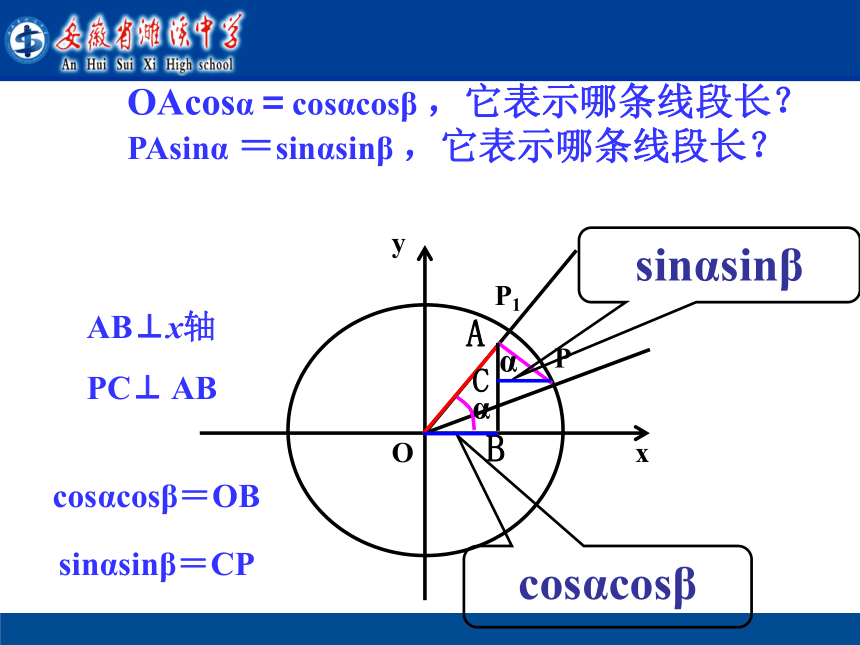
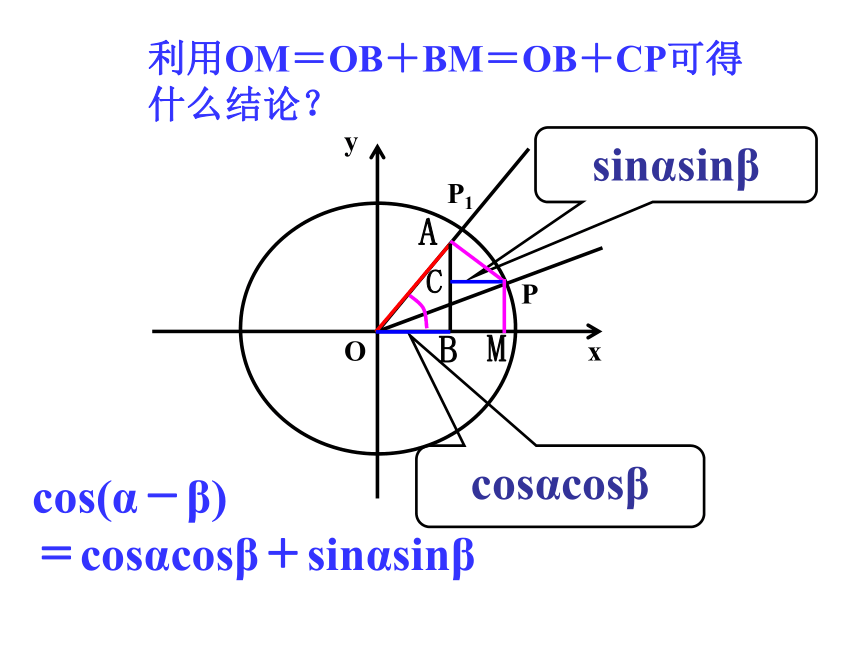
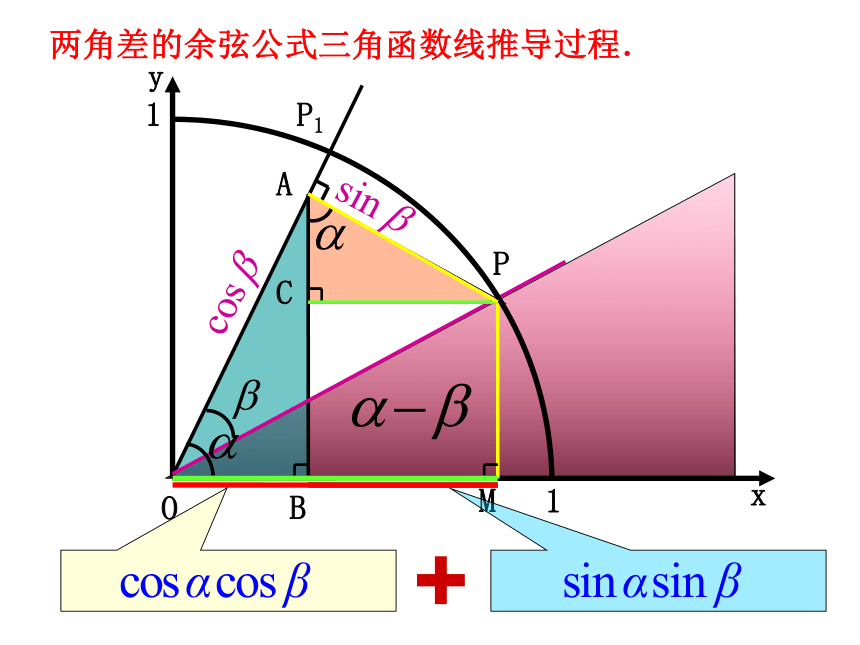
PAsinα =sinαsinβ ,它表示哪条线段长?sinαsinβcosαcosβcosαcosβ=OBsinαsinβ=CPAB⊥x轴PC⊥ ABαα利用OM=OB+BM=OB+CP可得什么结论?cos(α-β)
=cosαcosβ+sinαsinβxyPP1MBOAC+11两角差的余弦公式三角函数线推导过程.对于任意角α、β都有:需要注意的是:以上的推导过程是在α,β为锐角,且α>β的情况下成立的。那么此公式对任意α,β角都成立吗?答案是肯定的,但是需要进一步的推广,且推广的过程也是比较繁琐的,有兴趣的同学可以自己试一试,另外请大家课下探索其他的证明方法。记作探究:两角差的余弦公式的变化 思考1:若已知α+β和β的三角函数值,如何求cosα的值? cosα=cos[(α+β)-β]
=cos(α+β)cosβ+sin(α+β)sinβ. 思考2:利用α-(α-β)=β可得cosβ等于什么?cosβ=cos[α -(α-β)]
=cos(α-β)cosα+sin(α-β)sinα. 思考3:若cosα+cosβ=a,sinα+sinβ=b,则cos(α-β)等于什么? 思考4:若cosα-cosβ=a,sinα-sinβ=b,则cos(α-β)等于什么?解: cos15°=cos(45°-30°)= cos45°cos30°+sin45°sin30°∵∴方法一例1 利用差角余弦公式求cos15°的值。解: cos15°=cos(60°-45°)= cos60°cos45°+sin60°sin45°∵∴方法二做一做利用差角公式求值时,常常进行角的分拆与组合.即公式的变用.例21.两角差的余弦公式:2.已知一个角的正弦(或余弦)值,求该角的余弦(或正弦)值时, 要注意该角所在的象限,从而确定该角的三角函数值符号.3.在差角的余弦公式中, 运用时要注意角的变换如 , 等.同时,公式的应用具有灵活性,解题时要注意正向、逆向和变式形式的选择.课堂小结思考交流:
由公式 出发,你能推导出两角和与
差的三角函数的其他公式。
下面就一起探讨两角差的余弦公式α-β 如图,设α,β为锐角,且α>β,角α的终边与单位圆的交点为P1,∠P1OP=β,那么cos(α-β)表示哪条线段长?cos(α-β)
=OMαβ用三角函数线方法探究两角差的余弦公式 如何用线段分别表示sinβ和cosβ?sinβcosββOAcosα=cosαcosβ ,它表示哪条线段长?
PAsinα =sinαsinβ ,它表示哪条线段长?sinαsinβcosαcosβcosαcosβ=OBsinαsinβ=CPAB⊥x轴PC⊥ ABαα利用OM=OB+BM=OB+CP可得什么结论?cos(α-β)
=cosαcosβ+sinαsinβxyPP1MBOAC+11两角差的余弦公式三角函数线推导过程.对于任意角α、β都有:需要注意的是:以上的推导过程是在α,β为锐角,且α>β的情况下成立的。那么此公式对任意α,β角都成立吗?答案是肯定的,但是需要进一步的推广,且推广的过程也是比较繁琐的,有兴趣的同学可以自己试一试,另外请大家课下探索其他的证明方法。记作探究:两角差的余弦公式的变化 思考1:若已知α+β和β的三角函数值,如何求cosα的值? cosα=cos[(α+β)-β]
=cos(α+β)cosβ+sin(α+β)sinβ. 思考2:利用α-(α-β)=β可得cosβ等于什么?cosβ=cos[α -(α-β)]
=cos(α-β)cosα+sin(α-β)sinα. 思考3:若cosα+cosβ=a,sinα+sinβ=b,则cos(α-β)等于什么? 思考4:若cosα-cosβ=a,sinα-sinβ=b,则cos(α-β)等于什么?解: cos15°=cos(45°-30°)= cos45°cos30°+sin45°sin30°∵∴方法一例1 利用差角余弦公式求cos15°的值。解: cos15°=cos(60°-45°)= cos60°cos45°+sin60°sin45°∵∴方法二做一做利用差角公式求值时,常常进行角的分拆与组合.即公式的变用.例21.两角差的余弦公式:2.已知一个角的正弦(或余弦)值,求该角的余弦(或正弦)值时, 要注意该角所在的象限,从而确定该角的三角函数值符号.3.在差角的余弦公式中, 运用时要注意角的变换如 , 等.同时,公式的应用具有灵活性,解题时要注意正向、逆向和变式形式的选择.课堂小结思考交流:
由公式 出发,你能推导出两角和与
差的三角函数的其他公式。
