《数列中an和Sn的关系》 课件(26张PPT)
文档属性
| 名称 | 《数列中an和Sn的关系》 课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 746.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-02 00:00:00 | ||
图片预览








文档简介
课件26张PPT。数列中an与sn的关系普通高中课程标准实验教科书数学 必修五 第二章数列【课前回顾 夯实基础】我们前面已经学过等差数列、等比数列(1)可以由 an=f(n),求出Sn(2)可以由 Sn=f(n), 求出an例如: 等差数列中有
等比数列中有例如: 已知Sn=n2+4n ,可以求an若含有an与Sn的关系式,如何求出an或Sn呢?问题?清华大学准备拿出一定的经费m万元,奖励参与科研获奖的学生,奖励方式如下:
第一名得全部奖金的一半多一万元,
第二名得剩下的一半多一万元,
· · · · · ·
以名次类推都得到剩下的一半多一万元,
假设获得第n名的同学获得奖金数为an元,其中n=1,2,3 ,· · ·
前n名次的同学获得奖金总和为Sn元。
你能利用数列知识建立一个数学模型,来解决你可以拿多少奖金这个问题吗?【问题引入 数学建模】清华大学校方准备拿出一定的经费m万元,奖励参与科研获奖的学生,奖励方式如下:
第一名得全部奖金的一半多一万元,
第二名得剩下的一半多一万元,
· · · · · ·
以名次类推都得到剩下的一半多一万元,
假设获得第n名的同学获得奖金数为an元,其中n=1,2,3 ,· · ·
前n名次的同学获得奖金总和为Sn元。
你能利用数列知识建立一个数学模型,来解决你可以拿多少奖金这个问题吗?【问题引入 数学建模】数学建模 就是根据实际问题来建立数学模型,对数学模型来进行求解,然后根据结果去解决实际问题。或【知识总结 夯实基础】 一、项式 an 与和式sn的关系 探究问题:
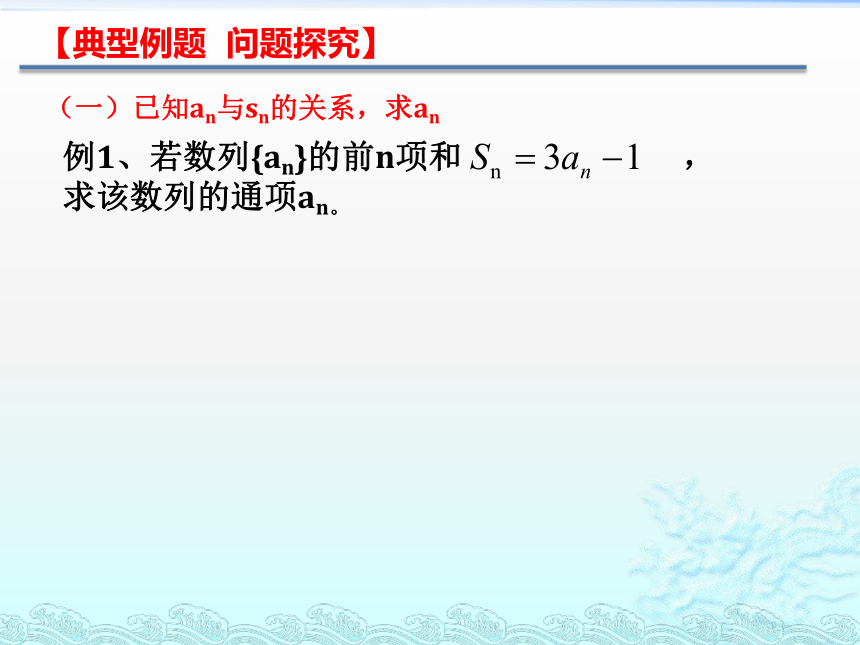
已知an与Sn的关系式,求an或Sn。例1、若数列{an}的前n项和 ,
求该数列的通项an。 (一)已知an与sn的关系,求an【典型例题 问题探究】例1、若数列{an}的前n项和 ,
求该数列的通项an。 (一)已知an与sn的关系,求an【典型例题 问题探究】? 这是一个什么类型的问题??如何实现从条件到结论的转化??怎样转化?类型求数列通项an已知条件为an与sn的关系式特征转化Snan例1、若数列{an}的前n项和 ,
求该数列的通项an。 解:当n=1时,得 当n ≥ 2时,即则有例1、若数列{an}的前n项和 ,
求该数列的通项an。 解:当n=1时,得 当n ≥ 2时,即则有数列{an}是首项为 ,公比为 的等比数列,首项为a1例1、若数列{an}的前n项和 ,
求该数列的通项an。 【变化条件 突破难点】变式1:若将上述条件改为 ,且
如何求该数列的通项an。 变式2:若将上述条件改为 且
你能用几种方法求该数列的通项an请比较条件的细微不同,
对所求的结果有何影响?变式1:若将上述条件改为 ,且
如何求该数列的通项an。 ①②由①-②得:an=解:依题意得:得:即数列{an}从第二项起,是首项为 a2 ,公比为4/3 的等比数列,【变式条件 突破难点】变式2:若将上述条件改为 且
你能用几种方法求该数列的通项an方法1:作差法: an=sn-sn-1(n ≥2)【变式条件 突破难点】数列{an}从第二项起,是首项为 a2 ,公比为4/3 的等比数列,变式2:若将上述条件改为 且
你能用几种方法求该数列的通项an方法2: 作商法:【变式条件 突破难点】变式2:若将上述条件改为 且
你能用几种方法求该数列的通项an方法3:迭代法:
探究下列方法,请填空:【变式条件 突破难点】??变化 2 :若将上述条件改为 且
你能用几种方法求该数列的通项an【变式条件 突破难点】方法4:递推法:
探究下列方法,请填空:变式2 :若将上述条件改为 且
你能用几种方法求该数列的通项an【变式条件 突破难点】方法5:构造法:再转求an即可。变式2:若将上述条件改为 且
你能用几种方法求该数列的通项an方法1:作差消Sn法: an=sn-sn-1(n ≥2)方法2: 作商法:方法5: 消an法(间接构造新数列):【变式条件 突破难点】方法3:恒成立的思想(迭代法)方法4:恒成立的思想(递推法)例2、若数列{an}中a1=1,前n项和 sn满足:
, 求sn。 【典型例题 问题探究】例2、若数列{an}中a1=1,前n项和 sn满足:
,求该数列的通项an。 解:由得则有 即:【典型例题 问题探究】数列 是首项为1 ,公差为-2的等差数列,类题演练:若数列{an}中a1=1,前n项和 sn满足:
, 试问 是什么数列,并求sn。 例2、若数列{an}中a1=1,前n项和 sn满足:
, 求sn。 【典型例题 问题探究】清华大学校方准备拿出一定的经费m万元,奖励参与科研获奖的学生,奖励方式如下:
第一名得全部奖金的一半多一万元,
第二名得剩下的一半多一万元,
· · · · · ·
以名次类推都得到剩下的一半多一万元,
假设获得第n名的同学获得奖金数为an元,其中n=1,2,3 ,· · ·
前n名次的同学获得奖金总和为Sn元。
你能利用数列知识建立一个数学模型,来解决你可以拿多少奖金这个问题吗?【数学模型 解决问题】若到了第10名恰好资金分完了,那么清华大学校方共拿出多少万元资金进行奖励?① ②①- ②,得:【数学模型 解决问题】解得:m=2046故清华大学校方共拿出2046万元资金进行奖励。消sn法:【数学模型 解决问题】消an法:【类题演练 方法发散】练习1 已知等差数列{an}的前n项和是Sn,a1=1,S3=6,正项
数列{bn}满足: ,求{bn}的通项公式。练习2【方法小结 类题通法】 一、项式 an 与和式sn的关系 二、注意:讨论n=1的情况“和”变“项”“项”变“和”三、常见思想方法:
方程组的思想;恒成立的思想;迭代的思想函数消元的思想【作业布置 课后拓展】作业2 作业1 正项数列{an}的前n项和是Sn,已知a1=3,,求数列{an}的通项公式。
等比数列中有例如: 已知Sn=n2+4n ,可以求an若含有an与Sn的关系式,如何求出an或Sn呢?问题?清华大学准备拿出一定的经费m万元,奖励参与科研获奖的学生,奖励方式如下:
第一名得全部奖金的一半多一万元,
第二名得剩下的一半多一万元,
· · · · · ·
以名次类推都得到剩下的一半多一万元,
假设获得第n名的同学获得奖金数为an元,其中n=1,2,3 ,· · ·
前n名次的同学获得奖金总和为Sn元。
你能利用数列知识建立一个数学模型,来解决你可以拿多少奖金这个问题吗?【问题引入 数学建模】清华大学校方准备拿出一定的经费m万元,奖励参与科研获奖的学生,奖励方式如下:
第一名得全部奖金的一半多一万元,
第二名得剩下的一半多一万元,
· · · · · ·
以名次类推都得到剩下的一半多一万元,
假设获得第n名的同学获得奖金数为an元,其中n=1,2,3 ,· · ·
前n名次的同学获得奖金总和为Sn元。
你能利用数列知识建立一个数学模型,来解决你可以拿多少奖金这个问题吗?【问题引入 数学建模】数学建模 就是根据实际问题来建立数学模型,对数学模型来进行求解,然后根据结果去解决实际问题。或【知识总结 夯实基础】 一、项式 an 与和式sn的关系 探究问题:
已知an与Sn的关系式,求an或Sn。例1、若数列{an}的前n项和 ,
求该数列的通项an。 (一)已知an与sn的关系,求an【典型例题 问题探究】例1、若数列{an}的前n项和 ,
求该数列的通项an。 (一)已知an与sn的关系,求an【典型例题 问题探究】? 这是一个什么类型的问题??如何实现从条件到结论的转化??怎样转化?类型求数列通项an已知条件为an与sn的关系式特征转化Snan例1、若数列{an}的前n项和 ,
求该数列的通项an。 解:当n=1时,得 当n ≥ 2时,即则有例1、若数列{an}的前n项和 ,
求该数列的通项an。 解:当n=1时,得 当n ≥ 2时,即则有数列{an}是首项为 ,公比为 的等比数列,首项为a1例1、若数列{an}的前n项和 ,
求该数列的通项an。 【变化条件 突破难点】变式1:若将上述条件改为 ,且
如何求该数列的通项an。 变式2:若将上述条件改为 且
你能用几种方法求该数列的通项an请比较条件的细微不同,
对所求的结果有何影响?变式1:若将上述条件改为 ,且
如何求该数列的通项an。 ①②由①-②得:an=解:依题意得:得:即数列{an}从第二项起,是首项为 a2 ,公比为4/3 的等比数列,【变式条件 突破难点】变式2:若将上述条件改为 且
你能用几种方法求该数列的通项an方法1:作差法: an=sn-sn-1(n ≥2)【变式条件 突破难点】数列{an}从第二项起,是首项为 a2 ,公比为4/3 的等比数列,变式2:若将上述条件改为 且
你能用几种方法求该数列的通项an方法2: 作商法:【变式条件 突破难点】变式2:若将上述条件改为 且
你能用几种方法求该数列的通项an方法3:迭代法:
探究下列方法,请填空:【变式条件 突破难点】??变化 2 :若将上述条件改为 且
你能用几种方法求该数列的通项an【变式条件 突破难点】方法4:递推法:
探究下列方法,请填空:变式2 :若将上述条件改为 且
你能用几种方法求该数列的通项an【变式条件 突破难点】方法5:构造法:再转求an即可。变式2:若将上述条件改为 且
你能用几种方法求该数列的通项an方法1:作差消Sn法: an=sn-sn-1(n ≥2)方法2: 作商法:方法5: 消an法(间接构造新数列):【变式条件 突破难点】方法3:恒成立的思想(迭代法)方法4:恒成立的思想(递推法)例2、若数列{an}中a1=1,前n项和 sn满足:
, 求sn。 【典型例题 问题探究】例2、若数列{an}中a1=1,前n项和 sn满足:
,求该数列的通项an。 解:由得则有 即:【典型例题 问题探究】数列 是首项为1 ,公差为-2的等差数列,类题演练:若数列{an}中a1=1,前n项和 sn满足:
, 试问 是什么数列,并求sn。 例2、若数列{an}中a1=1,前n项和 sn满足:
, 求sn。 【典型例题 问题探究】清华大学校方准备拿出一定的经费m万元,奖励参与科研获奖的学生,奖励方式如下:
第一名得全部奖金的一半多一万元,
第二名得剩下的一半多一万元,
· · · · · ·
以名次类推都得到剩下的一半多一万元,
假设获得第n名的同学获得奖金数为an元,其中n=1,2,3 ,· · ·
前n名次的同学获得奖金总和为Sn元。
你能利用数列知识建立一个数学模型,来解决你可以拿多少奖金这个问题吗?【数学模型 解决问题】若到了第10名恰好资金分完了,那么清华大学校方共拿出多少万元资金进行奖励?① ②①- ②,得:【数学模型 解决问题】解得:m=2046故清华大学校方共拿出2046万元资金进行奖励。消sn法:【数学模型 解决问题】消an法:【类题演练 方法发散】练习1 已知等差数列{an}的前n项和是Sn,a1=1,S3=6,正项
数列{bn}满足: ,求{bn}的通项公式。练习2【方法小结 类题通法】 一、项式 an 与和式sn的关系 二、注意:讨论n=1的情况“和”变“项”“项”变“和”三、常见思想方法:
方程组的思想;恒成立的思想;迭代的思想函数消元的思想【作业布置 课后拓展】作业2 作业1 正项数列{an}的前n项和是Sn,已知a1=3,,求数列{an}的通项公式。
