1.1.1 正弦定理 课件(28张PPT)
文档属性
| 名称 | 1.1.1 正弦定理 课件(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 790.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-02 22:13:36 | ||
图片预览





文档简介
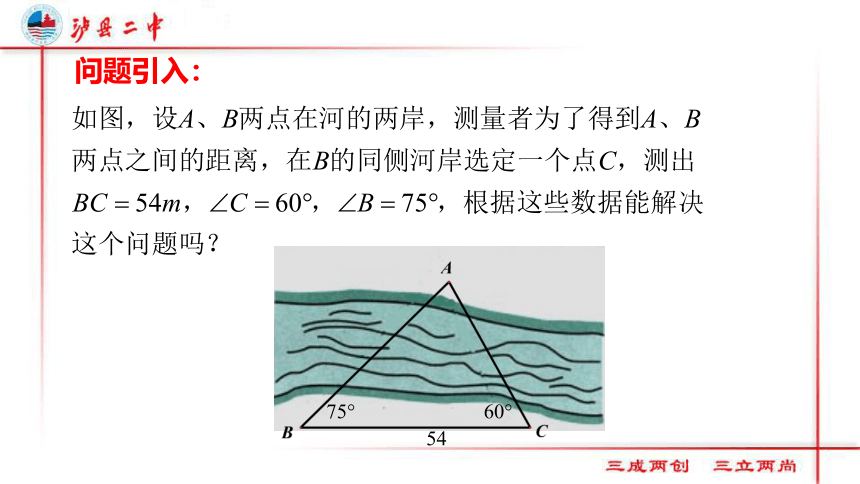
课件16张PPT。1.1.1 正弦定理必修五:第一章 解三角形天文测量 航海测量 地质测量1671年,两个法国天文学家测出地球与月球之间距离大约为385400Km,他们是怎样测出两者之间距离的呢?问题引入:复习回顾:直角三角形中边与角的数量关系小组讨论如何证明?小组讨论探究二:能否用其他方法证明:
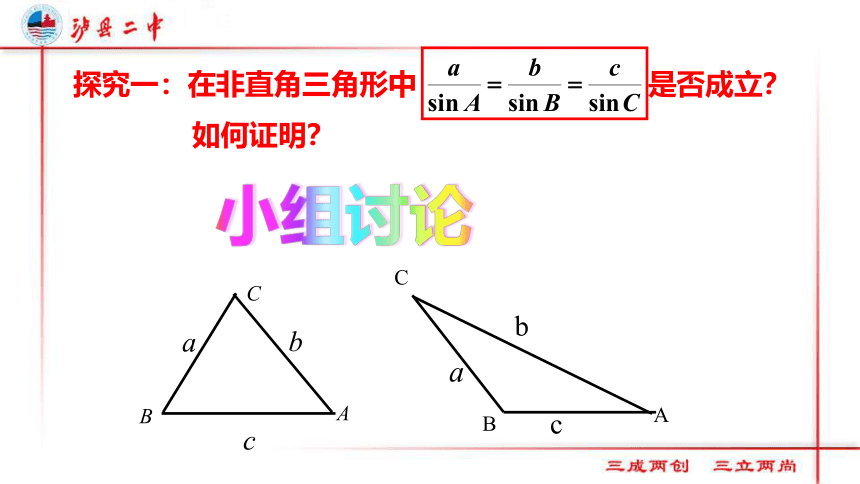
在非直角三角形中 成立?
如何证明? 正弦定理 在一个三角形中,各边和它所对角的正弦的比相等,即变形: 正弦定理 在一个三角形中,各边和它所对角的正弦的比相等,即 一般地,把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素.已知三角形的几个元素求其他元素的过程叫解三角形. 结构特征:含三角形三边及三角 对称美
描述了三角形中边与角的数量关系已知三角形的任意两边与其中一边的对角已知三角形任意两角与一边思考:正弦定理可以解决哪些解三角形问题?方程思想:问题再现:已知任意两角与一边已知任意两边与其中一边的对角定理应用:(1)已知三角形的任意两个角与一边
(2)已知三角形的任意两边与其中一边的对角 1、本节课我们学习了哪些知识?2、正弦定理可以解决哪些解三角形问题?3、体现了哪些数学思想方法?课堂总结:化归与转化思想 方程思想
数形结合思想 分类讨论思想课后思考: 2、在三角形中有“大边对大角,小边对小角”原理,如何利用正弦定理进行理论解释? 书上8-9页 《三角形的进一步讨论》课后作业:课后作业题单 1、还可以用其它方法证明正弦定理吗? 3、已知两边和其中一边的对角,求其他边和角时,三角形什么情况下有一解,二解,无解?谢谢观看 欢迎指导!证明:作外接圆O,过B作直径BC′,连接AC′,
在非直角三角形中 成立?
如何证明? 正弦定理 在一个三角形中,各边和它所对角的正弦的比相等,即变形: 正弦定理 在一个三角形中,各边和它所对角的正弦的比相等,即 一般地,把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素.已知三角形的几个元素求其他元素的过程叫解三角形. 结构特征:含三角形三边及三角 对称美
描述了三角形中边与角的数量关系已知三角形的任意两边与其中一边的对角已知三角形任意两角与一边思考:正弦定理可以解决哪些解三角形问题?方程思想:问题再现:已知任意两角与一边已知任意两边与其中一边的对角定理应用:(1)已知三角形的任意两个角与一边
(2)已知三角形的任意两边与其中一边的对角 1、本节课我们学习了哪些知识?2、正弦定理可以解决哪些解三角形问题?3、体现了哪些数学思想方法?课堂总结:化归与转化思想 方程思想
数形结合思想 分类讨论思想课后思考: 2、在三角形中有“大边对大角,小边对小角”原理,如何利用正弦定理进行理论解释? 书上8-9页 《三角形的进一步讨论》课后作业:课后作业题单 1、还可以用其它方法证明正弦定理吗? 3、已知两边和其中一边的对角,求其他边和角时,三角形什么情况下有一解,二解,无解?谢谢观看 欢迎指导!证明:作外接圆O,过B作直径BC′,连接AC′,
