1.1.1 正弦定理 课件(30张PPT)
文档属性
| 名称 | 1.1.1 正弦定理 课件(30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-02 00:00:00 | ||
图片预览










文档简介
课件30张PPT。第一章 解三角形第一节 正弦定理人教B版2003课标版必修五课题引入 在数学发展史上,受到天文测量、航海测量和理理测量等方面实践活动的推动,解三角形的理论得到不断发展,并用于解决许多测量问题怎样才能测出它有多高呢?创设情景 引入课题.C.B.A
为了测定河岸A点到对岸C点的距离,在岸边选定1公里长的基线AB,并测得∠ABC=120o,∠BAC=45o,如何求A、C两点的距离?正弦定理
(第一课时)复习三角形中的边角关系1、角的关系
2、边的关系
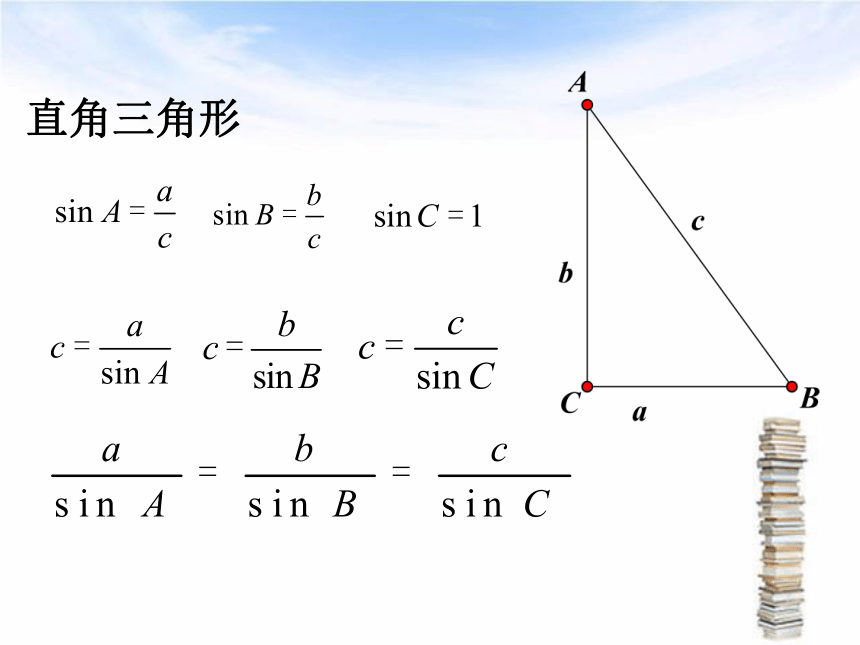
3、边角关系(一)三角形中的边角关系 (二)直角三角形中的边角关系 (角C为直角)1、角的关系
2、边的关系
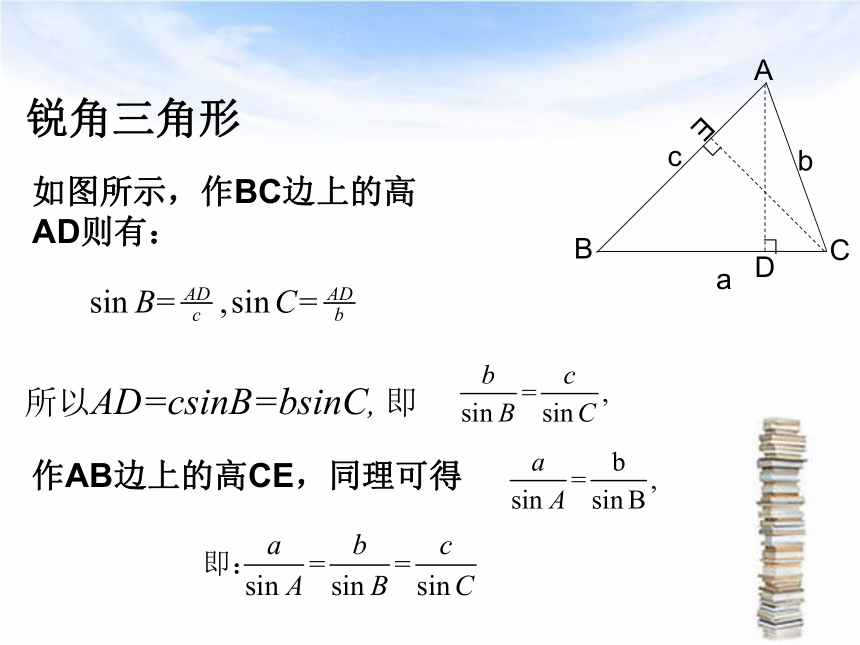
3、边角关系直角三角形即:锐角和钝角三角形中,是否也有同样的边角关系?探索:直角三角形的边角关系式对任意三角形是否成立?(1)直角三角形中,已证得结论成立锐角三角形如图所示,作BC边上的高AD则有:所以AD=csinB=bsinC, 即a锐角三角形如图所示,作BC边上的高AD则有:所以AD=csinB=bsinC, 即作AB边上的高CE,同理可得a(1)直角三角形中,已证得结论成立(2)锐角三角形中,已证得结论成立钝角三角形如图所示,过点A作AD⊥BC,交BC延长线于D,所以AD=csinB=bsinC, 即a钝角三角形如图所示,过点A作AD⊥BC,交BC延长线于D,所以AD=csinB=bsinC, 即a作AB边上的高CE,同理可得(1)直角三角形中,已证得结论成立(2)锐角三角形中,已证得结论成立(3)钝角三角形中,已证得结论成立正弦定理探究=求证:=2R(2R为△ABC外接圆直径)作外接圆O,证明:过B作直径BC/,连AC/,例1nn例1在△ABC 中,已知c = 10,A = 45。, C = 30。求 a , b 及角B.变式1:若将本题中c=10改为a=10,能不能求出c,b及角B?变式2:若将本题中c=10改为b=10,能不能求出c,a及角B?已知两角和任意边,
求其他两边和一角YESYES例2 在△ABC 中,已知 a=16, b= , A=30° .求角B,C和边c得B=60°,或B=120°C=90°当B=120°时C=30°例2 在△ABC 中已知a=16, b= , A=30° .求角B,C和边c变式1:若将本题中A=30°改为B=30° ,能不能求出角A,C及边c?变式2:若将本题中A=30°改为C=30° ,能不能求出角A,B及边c?YESNO已知两边和其中一边
的对角,求其他边和角正弦定理的应用总结(1)已知两边和其中一边的对角,求另一边
的对角,进而可求其他的边和角.(2)已知两角和任意一边,求其他角和边.课堂小结=2R1、2、正弦定理的应用(解三角形)(1)已知两角及任意一边,求其他角和边(2)已知两边及其中一边的对角,求其他
角和边正弦定理 内容:应用已知两角和一边
已知两边和其中一边对角1)探求应用向量方法证明正弦定理 2)书面作业布置P4练习1、2The end,thank you!
为了测定河岸A点到对岸C点的距离,在岸边选定1公里长的基线AB,并测得∠ABC=120o,∠BAC=45o,如何求A、C两点的距离?正弦定理
(第一课时)复习三角形中的边角关系1、角的关系
2、边的关系
3、边角关系(一)三角形中的边角关系 (二)直角三角形中的边角关系 (角C为直角)1、角的关系
2、边的关系
3、边角关系直角三角形即:锐角和钝角三角形中,是否也有同样的边角关系?探索:直角三角形的边角关系式对任意三角形是否成立?(1)直角三角形中,已证得结论成立锐角三角形如图所示,作BC边上的高AD则有:所以AD=csinB=bsinC, 即a锐角三角形如图所示,作BC边上的高AD则有:所以AD=csinB=bsinC, 即作AB边上的高CE,同理可得a(1)直角三角形中,已证得结论成立(2)锐角三角形中,已证得结论成立钝角三角形如图所示,过点A作AD⊥BC,交BC延长线于D,所以AD=csinB=bsinC, 即a钝角三角形如图所示,过点A作AD⊥BC,交BC延长线于D,所以AD=csinB=bsinC, 即a作AB边上的高CE,同理可得(1)直角三角形中,已证得结论成立(2)锐角三角形中,已证得结论成立(3)钝角三角形中,已证得结论成立正弦定理探究=求证:=2R(2R为△ABC外接圆直径)作外接圆O,证明:过B作直径BC/,连AC/,例1nn例1在△ABC 中,已知c = 10,A = 45。, C = 30。求 a , b 及角B.变式1:若将本题中c=10改为a=10,能不能求出c,b及角B?变式2:若将本题中c=10改为b=10,能不能求出c,a及角B?已知两角和任意边,
求其他两边和一角YESYES例2 在△ABC 中,已知 a=16, b= , A=30° .求角B,C和边c得B=60°,或B=120°C=90°当B=120°时C=30°例2 在△ABC 中已知a=16, b= , A=30° .求角B,C和边c变式1:若将本题中A=30°改为B=30° ,能不能求出角A,C及边c?变式2:若将本题中A=30°改为C=30° ,能不能求出角A,B及边c?YESNO已知两边和其中一边
的对角,求其他边和角正弦定理的应用总结(1)已知两边和其中一边的对角,求另一边
的对角,进而可求其他的边和角.(2)已知两角和任意一边,求其他角和边.课堂小结=2R1、2、正弦定理的应用(解三角形)(1)已知两角及任意一边,求其他角和边(2)已知两边及其中一边的对角,求其他
角和边正弦定理 内容:应用已知两角和一边
已知两边和其中一边对角1)探求应用向量方法证明正弦定理 2)书面作业布置P4练习1、2The end,thank you!
