1.1.1 正弦定理 课件(22张PPT)
文档属性
| 名称 | 1.1.1 正弦定理 课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 324.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-08-02 00:00:00 | ||
图片预览







文档简介
课件22张PPT。1.1.1 正弦定理人教版必修5 第一章 解三角形一、回顾与引入引入:给定一个三角形的两角及一边,三角形唯一确定吗?如何求其他边与角呢?
一、回顾与引入回顾三角形的相关知识:
“大边对大角,大角对大边”,这是定性地研究三角形中的边角关系,我们能否从定量的角度研究三角形中的边角关系呢?即我们是否能得到这个边、角关系准确量化的表示呢?二、探究新知
探究1:(1)探究直角三角形中的边角关系.二、探究新知
探究1:(2)对于一般的三角形,以上关系式是否还成立?二、探究新知
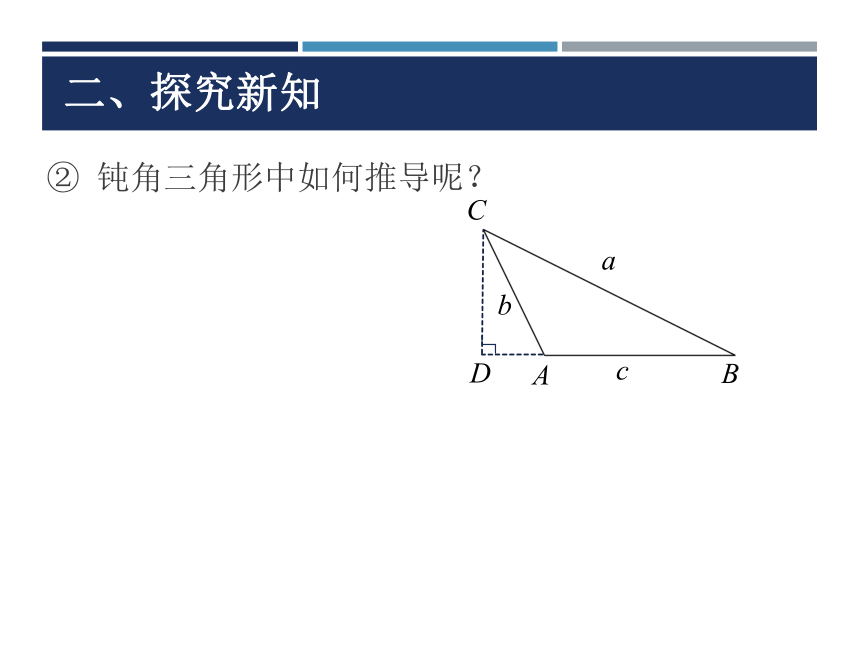
② 钝角三角形中如何推导呢?二、探究新知
正弦定理:注:正弦定理的本质是“定量地描述三角形边角之间的关系”,是“大边对大角,大角对大边”这一性质一种准确量化的表示.一般三角形转化为直角三角形,这体现了化归思想.化归不仅是一种重要的解题思想,也是一种最基本的思维策略,更是一种有效的数学思维方式.二、探究新知
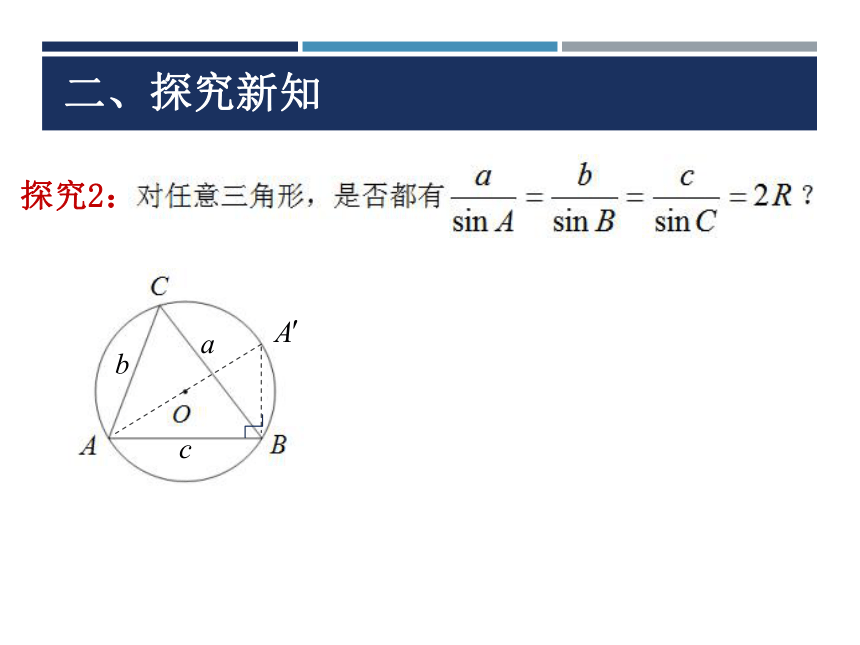
问题1:二、探究新知探究2:
三、理解定理,解决问题
问题:正弦定理可以解决哪些问题呢?已知三角形两角及一边,求另一角与另两边?方程思想
知三求一三角形两边及其中一边的对角,求另一边与另两角?思考:对比分析例2--变式3的题目条件,对比解的情况.
已知两边及其中一边对角,三角形可能无解,一解,二解.
已知两角及一边,会出现这种情况吗?两角及一边对应相等的两个三角形全等;
两边及其中一边对角分别对应相等,无法判断两三角形全等.
问题2:如何从形的角度解释两解、一解、无解的原因?方法总结:已知两边及其中一边对角,判断三角形解的个数的方法:法一:应用三角形中大边对大角的性质及正弦函数的值域 判断解的个数;
法二:利用图形.四、课堂小结
这节课你有哪些收获?(1)学习了正弦定理,正弦定理可以解决的问题类型:
① 已知三角形的任意两角及一边,解三角形;
② 已知三角形的任意两边及其中一边的对角,解三角形.
(2)在正弦定理的发现及证明过程中,蕴含着丰富的思想方法,我们不仅收获着结论,也学习了研究问题的思想方法,如由特殊到一般的归纳思想方法,化归思想,以及数形结合思想,分类讨论思想等;
(3)正弦定理刻画了边角之间具体的数量关系,实现了边角之间的互化,这一部分我们在作业中再补充;
五、作业布置
《成才》:
A组:1--10
B组:1,3,4,5,6
C组:1谢谢!
一、回顾与引入回顾三角形的相关知识:
“大边对大角,大角对大边”,这是定性地研究三角形中的边角关系,我们能否从定量的角度研究三角形中的边角关系呢?即我们是否能得到这个边、角关系准确量化的表示呢?二、探究新知
探究1:(1)探究直角三角形中的边角关系.二、探究新知
探究1:(2)对于一般的三角形,以上关系式是否还成立?二、探究新知
② 钝角三角形中如何推导呢?二、探究新知
正弦定理:注:正弦定理的本质是“定量地描述三角形边角之间的关系”,是“大边对大角,大角对大边”这一性质一种准确量化的表示.一般三角形转化为直角三角形,这体现了化归思想.化归不仅是一种重要的解题思想,也是一种最基本的思维策略,更是一种有效的数学思维方式.二、探究新知
问题1:二、探究新知探究2:
三、理解定理,解决问题
问题:正弦定理可以解决哪些问题呢?已知三角形两角及一边,求另一角与另两边?方程思想
知三求一三角形两边及其中一边的对角,求另一边与另两角?思考:对比分析例2--变式3的题目条件,对比解的情况.
已知两边及其中一边对角,三角形可能无解,一解,二解.
已知两角及一边,会出现这种情况吗?两角及一边对应相等的两个三角形全等;
两边及其中一边对角分别对应相等,无法判断两三角形全等.
问题2:如何从形的角度解释两解、一解、无解的原因?方法总结:已知两边及其中一边对角,判断三角形解的个数的方法:法一:应用三角形中大边对大角的性质及正弦函数的值域 判断解的个数;
法二:利用图形.四、课堂小结
这节课你有哪些收获?(1)学习了正弦定理,正弦定理可以解决的问题类型:
① 已知三角形的任意两角及一边,解三角形;
② 已知三角形的任意两边及其中一边的对角,解三角形.
(2)在正弦定理的发现及证明过程中,蕴含着丰富的思想方法,我们不仅收获着结论,也学习了研究问题的思想方法,如由特殊到一般的归纳思想方法,化归思想,以及数形结合思想,分类讨论思想等;
(3)正弦定理刻画了边角之间具体的数量关系,实现了边角之间的互化,这一部分我们在作业中再补充;
五、作业布置
《成才》:
A组:1--10
B组:1,3,4,5,6
C组:1谢谢!
